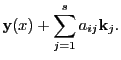34.2 Runge Kutta Integration
The RK integration scheme starts from an initial set of first order ODE dependent variable
values 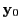 and advances the ODE solution
and advances the ODE solution 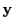 through well defined steps in the
independent variable
through well defined steps in the
independent variable  . Control of the dependent variable errors allows for optimum step size control.
We describe here the embedded RK schemes, which use the same intermediate vectors
. Control of the dependent variable errors allows for optimum step size control.
We describe here the embedded RK schemes, which use the same intermediate vectors 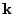 to get an
estimate of the error vector
to get an
estimate of the error vector 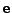 . An embedded RK step can be represented by the following equations:
. An embedded RK step can be represented by the following equations:
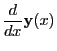 |
 |
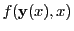 |
(34.1) |
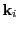 |
 |
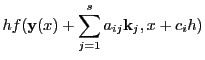 |
(34.2) |
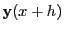 |
 |
![$\displaystyle {\bf y}(x)+\sum_{i=1}^sb_i{\bf k}_i + O[h^{p+2}]$](img3340.png) |
(34.3) |
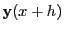 |
 |
![$\displaystyle {\bf y}(x)+\sum_{i=1}^sb_i^*{\bf k}_i + O[h^{p+1}]$](img3341.png) |
(34.4) |
 |
 |
![$\displaystyle \sum_{i=1}^s(b_i-b_i^*){\bf k}_i + O[h^{p+1}]$](img3342.png) |
(34.5) |
Here 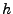 denotes the step size and
denotes the step size and 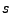 is the size of the embedded RK scheme.
Each particular embedded RK scheme is characterized by the four sets of coefficients
is the size of the embedded RK scheme.
Each particular embedded RK scheme is characterized by the four sets of coefficients
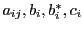 , which can be arranged into a table known as a Butcher tableau:
The coefficients
, which can be arranged into a table known as a Butcher tableau:
The coefficients 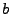 and
and 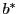 correspond to RK methods of order
correspond to RK methods of order 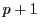 and
and 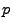 , from which
the error vector is constructed via equation 34.5. If only the strict
lower triangle of the
, from which
the error vector is constructed via equation 34.5. If only the strict
lower triangle of the 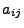 values are non-zero, then the embedded RK scheme is explicit.
Otherwise we have an implicit scheme. Explicit RK schemes are much easier to solve, because
all intermediate
values are non-zero, then the embedded RK scheme is explicit.
Otherwise we have an implicit scheme. Explicit RK schemes are much easier to solve, because
all intermediate 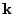 vectors can be evaluated one after another using previously evaluated
vectors can be evaluated one after another using previously evaluated
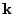 vectors. Implicit RK schemes on the other hand have to be solved in an iteratively
fashion and are much more expensive. FLASH4 currently has only explicit RK schemes implemented.
Error control on each RK step is done by passing a maximum allowed absolute error vector
vectors. Implicit RK schemes on the other hand have to be solved in an iteratively
fashion and are much more expensive. FLASH4 currently has only explicit RK schemes implemented.
Error control on each RK step is done by passing a maximum allowed absolute error vector
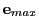 corresponding to each of the dependent variables in
corresponding to each of the dependent variables in 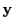 .
Step size control is currently implemented using information from the obtained error vector
.
Step size control is currently implemented using information from the obtained error vector
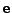 after the RK step and the maximum error vector
after the RK step and the maximum error vector
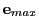 . Using the fact
that the error scales as
. Using the fact
that the error scales as
![$ {\bf O}[h^{p+1}]$](img3366.png) due to the lower
due to the lower 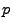 order embedded RK method, the new step
size
order embedded RK method, the new step
size 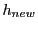 is adjusted from the old step size
is adjusted from the old step size 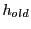 as follows
as follows
and used as the next trial step size. A safety factor (typically 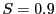 ) is used to account for
the fact that only the leading
) is used to account for
the fact that only the leading 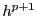 term from
term from
![$ {\bf O}[h^{p+1}]$](img3366.png) was used in deriving this
formula.
was used in deriving this
formula.
In some situations one needs an initial guess for the very first initial trial step size. This
can be done from the supplied ODE vector 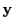 and the maximum allowed error vector
and the maximum allowed error vector
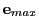 as follows. Consider the Taylor expansion of
as follows. Consider the Taylor expansion of
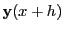 around
around  :
:
where
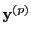 denotes the
denotes the 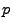 -th derivative of
-th derivative of 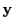 with respect to
with respect to  . The expansion
error
. The expansion
error
![$ {\bf O}[h^{p+1}]$](img3366.png) can be directly related to the
can be directly related to the
![$ {\bf O}[h^{p+1}]$](img3366.png) error of a RK method
of order
error of a RK method
of order 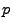 (cf. equation 34.4). As an approximation one can equate the absolute
value of the Taylor remainder term with the error goal of the RK method (i.e. plugging in formulas for
both
(cf. equation 34.4). As an approximation one can equate the absolute
value of the Taylor remainder term with the error goal of the RK method (i.e. plugging in formulas for
both
![$ {\bf O}[h^{p+1}]$](img3366.png) terms):
terms):
where
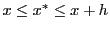 . Since we are dealing with an approximation, we further set
. Since we are dealing with an approximation, we further set 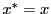 (this in effect approximates
(this in effect approximates
![$ {\bf O}[h^{p+1}]$](img3366.png) by its leading term and ignores the
by its leading term and ignores the 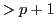 terms),
leading to
terms),
leading to
We then solve for 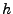 and take the minimum to satisfy all components.
To use this formula we need to evaluate the derivative. The following are second order central
difference formulas based on equal spacing
and take the minimum to satisfy all components.
To use this formula we need to evaluate the derivative. The following are second order central
difference formulas based on equal spacing 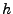 (not to be confused with the RK step size) between
functions:
(not to be confused with the RK step size) between
functions:
where the remainder term is equal to
with
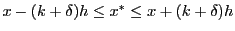 and
and
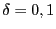 , depending on if one wants
even or odd higher order derivatives. For
, depending on if one wants
even or odd higher order derivatives. For 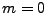 the derivatives are given in terms of the original
functions
the derivatives are given in terms of the original
functions
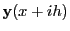 , whereas for
, whereas for 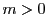 we get higher order derivatives from lower order
derivatives. These formulas can be derived by setting up a system of derivative linear equations from
the Taylor expansions of all the (derivative) functions
we get higher order derivatives from lower order
derivatives. These formulas can be derived by setting up a system of derivative linear equations from
the Taylor expansions of all the (derivative) functions
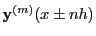 for a certain range of
for a certain range of 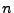 integers and solving these equations for the lowest derivatives (the
technique is discribed in J. Mathews, Computer Derivations of Numerical Differentiation Formulae,
International Journal of Mathematics Education in Science and Technology, Volume 34 No 2, pp.280-287).
The functions
integers and solving these equations for the lowest derivatives (the
technique is discribed in J. Mathews, Computer Derivations of Numerical Differentiation Formulae,
International Journal of Mathematics Education in Science and Technology, Volume 34 No 2, pp.280-287).
The functions
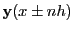 could in principle be obtained using the RK equation
34.3, but a much more economical approach would be to use the
1st derivatives (i.e. using
could in principle be obtained using the RK equation
34.3, but a much more economical approach would be to use the
1st derivatives (i.e. using 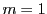 in equation 34.10). We have from
equation 34.1:
in equation 34.10). We have from
equation 34.1:
where, since the 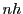 are small, the first order expansion of
are small, the first order expansion of
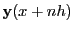 has been used.
Note the nested use of the derivative ODE function
has been used.
Note the nested use of the derivative ODE function 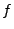 in equation 34.14. Since
the goal is to estimate
in equation 34.14. Since
the goal is to estimate
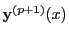 via equation 34.10, we
set
via equation 34.10, we
set
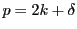 , from which
, from which 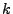 and
and 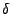 are uniquely determined.
are uniquely determined.
In practice it turns out that equation 34.10 is numerically very
unstable for higher order derivatives. We will use it only for estimating low order derivatives.
This leaves us with the problem of estimating higher order derivatives in equation
34.9. We follow ideas presented in J. Comp. Appl. Math. 18, 176-192 (1987).
To this end we first split the maximum error vector into an error base vector and an error fraction scalar
and have the user supplied both quantities. The purpose of this splitting is that we separate
the maximum error vector into an accuracy part (the 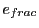 , typically of the order of
, typically of the order of
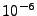 to
to 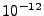 ) and a part which relates
to the magnitude of the vectors involved in the ODE (the
) and a part which relates
to the magnitude of the vectors involved in the ODE (the
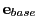 ). We further assume
that the user has sufficient knowledge about his ODE problem, such that he can construct these
two quantities obeying roughly the following inequalities:
). We further assume
that the user has sufficient knowledge about his ODE problem, such that he can construct these
two quantities obeying roughly the following inequalities:
With this choice of
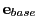 , all terms in equation 34.7
can be divided by
, all terms in equation 34.7
can be divided by
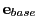 . If we now assume a smooth convergence of the Taylor
series and further postulate an exponential type decay between the individual
. If we now assume a smooth convergence of the Taylor
series and further postulate an exponential type decay between the individual
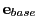 -rescaled Taylor terms (which all must be
-rescaled Taylor terms (which all must be 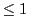 due to the assumptions
in equation 34.18)
due to the assumptions
in equation 34.18)
we can replace the higher order derivatives in equation 34.9 by lower
order ones and obtain:
Note the similar structure to equation 34.9. The higher order contribution
has been relegated to 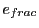 , which, due to the condition in equation 34.16,
leads to larger initial step size estimates for higher order RK schemes. In practice we calculate
step size estimates using only
, which, due to the condition in equation 34.16,
leads to larger initial step size estimates for higher order RK schemes. In practice we calculate
step size estimates using only 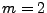 and
and 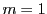 . In rare cases when all 1st and 2nd order derivatives
of
. In rare cases when all 1st and 2nd order derivatives
of
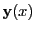 vanish, the (user supplied) default maximum step size estimate is used. This
maximum step size estimate can be given for example as a cell/domain size measure, when it is
clear that the RK stepper should not step beyond a cell or outside of the domain.
vanish, the (user supplied) default maximum step size estimate is used. This
maximum step size estimate can be given for example as a cell/domain size measure, when it is
clear that the RK stepper should not step beyond a cell or outside of the domain.
A separate RK stepping routine exists in FLASH4, which performs confined RK steps, which will
be explained next. Looking at equation 34.2, we see that for an RK step the
ODE function 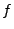 has to be evaluated repeatedly for several intermediate
has to be evaluated repeatedly for several intermediate 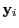 vectors
vectors
For certain applications it may not be possible to evaluate the ODE function at some of these
intermediate vectors due to lack of sufficient data. An example would be tracing the (classical)
path of a particle through a cell. Only the acceleration vector field of that particular cell is available.
If one of the position variables in 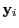 steps outside of the cell boundaries, the acceleration
vector at that point cannot be evaluated and the step size
steps outside of the cell boundaries, the acceleration
vector at that point cannot be evaluated and the step size 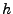 must be reduced. The confined RK stepping
routine needs extra boundary vectors corresponding to the variables in the
must be reduced. The confined RK stepping
routine needs extra boundary vectors corresponding to the variables in the 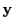 vectors. The boundary
vectors can be only a subset of all the
vectors. The boundary
vectors can be only a subset of all the 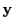 vector variables. Those variables which have no
corresponding boundary vector entries are assumed to be unbound. Since the boundaries might itself
depend on the variables in
vector variables. Those variables which have no
corresponding boundary vector entries are assumed to be unbound. Since the boundaries might itself
depend on the variables in 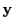 , the boundary vectors are transmitted to the confined RK stepper
as functions, which have to be designed by the user.
, the boundary vectors are transmitted to the confined RK stepper
as functions, which have to be designed by the user.
Currently there are five embedded explicit RK schemes implemented in FLASH, each corresponding to a particular
order: 2nd order Euler-Heun, 3rd order Bogacki-Shampine, 4th order Fehlberg, 5th order Fehlberg and
5th order Cash-Karp. Addition of other embedded RK schemes to the code is easy and consists only in
extending the existing Butcher tableau repository and adding the appropriate RK scheme keyword to the Runge Kutta
unit.
![]() and advances the ODE solution
and advances the ODE solution ![]() through well defined steps in the
independent variable
through well defined steps in the
independent variable ![]() . Control of the dependent variable errors allows for optimum step size control.
We describe here the embedded RK schemes, which use the same intermediate vectors
. Control of the dependent variable errors allows for optimum step size control.
We describe here the embedded RK schemes, which use the same intermediate vectors ![]() to get an
estimate of the error vector
to get an
estimate of the error vector ![]() . An embedded RK step can be represented by the following equations:
. An embedded RK step can be represented by the following equations:
![]() and the maximum allowed error vector
and the maximum allowed error vector
![]() as follows. Consider the Taylor expansion of
as follows. Consider the Taylor expansion of
![]() around
around ![]() :
:
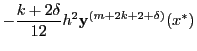
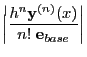
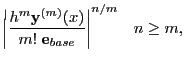
![]() has to be evaluated repeatedly for several intermediate
has to be evaluated repeatedly for several intermediate ![]() vectors
vectors