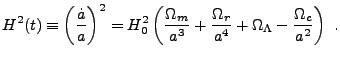22.1 Algorithms and Equations
The Cosmology unit makes several assumptions about the interpretation
of physical quantities that enable any hydrodynamics or materials
units written
for a non-expanding universe to work unmodified in a cosmological
context. All calculations are assumed to take place in comoving
coordinates
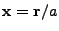 , where
, where 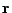 is a proper position
vector and
is a proper position
vector and 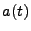 is the time-dependent cosmological scale factor.
The present epoch is defined to correspond to
is the time-dependent cosmological scale factor.
The present epoch is defined to correspond to 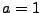 ; in the following
discussion we use
; in the following
discussion we use 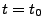 to refer to the age of the Universe at the
present epoch.
The gas velocity
to refer to the age of the Universe at the
present epoch.
The gas velocity 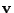 is taken to be the comoving peculiar
velocity
is taken to be the comoving peculiar
velocity
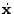 . The comoving gas density, pressure, temperature,
and internal energy are defined to be
. The comoving gas density, pressure, temperature,
and internal energy are defined to be
The quantities marked with a tilde, such as
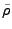 , are the
corresponding “proper” or physical quantities.
Note that, in terms of comoving quantities, the equation of state
has the same form as for the proper quantities in noncomoving
coordinates. For example, the perfect-gas equation of state is
, are the
corresponding “proper” or physical quantities.
Note that, in terms of comoving quantities, the equation of state
has the same form as for the proper quantities in noncomoving
coordinates. For example, the perfect-gas equation of state is
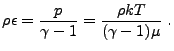 |
(22.2) |
With these definitions, the Euler equations of hydrodynamics can be
written in the form
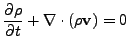 |
(22.3) |
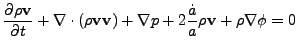 |
(22.4) |
![$\displaystyle {\partial\rho E\over\partial t} + \nabla\cdot[(\rho E + p){\bf v}...
...}\over a}[(3\gamma-1)\rho\epsilon + 2\rho v^2] + \rho{\bf v}\cdot\nabla\phi = 0$](img2348.png) |
(22.5) |
![$\displaystyle {\partial\rho\epsilon\over\partial t} + \nabla\cdot[(\rho\epsilon...
...\bf v}] -{\bf v}\cdot\nabla p + {{\dot a}\over a}(3\gamma-1)\rho\epsilon = 0 .$](img2349.png) |
(22.6) |
Here 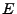 is the specific total energy,
is the specific total energy,
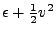 , and
, and
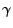 is the effective ratio of specific heats. The Cosmology
unit applies the terms involving
is the effective ratio of specific heats. The Cosmology
unit applies the terms involving 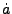 via the Cosmology_redshiftHydro
routine.
via the Cosmology_redshiftHydro
routine.
The comoving potential 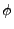 in the above equations
is the solution to the Poisson equation in the form
in the above equations
is the solution to the Poisson equation in the form
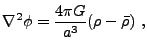 |
(22.7) |
where
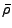 is the comoving mean matter density.
Note that, because of the presence of
is the comoving mean matter density.
Note that, because of the presence of 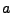 in (22.7),
the gravity units must explicitly divide their source terms by
in (22.7),
the gravity units must explicitly divide their source terms by 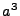 .
.
Units like the Gravity unit,
which require the scale factor or the redshift 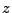 (
(
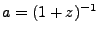 ),
can obtain the redshift via Cosmology_getRedshift, and use the
previous relation to obtain the scaling factor. The time represented by a
cosmological redshift can be obtained by a call to
Cosmology_redshiftToTime and passing it a cosmological redshift.
Note also that if a collisionless matter component (e.g.particles)
is also present, its density must be added to the gas density on the
right-hand side of (22.7). Accounting for particle masses in density
is handled by the Gravity unit.
),
can obtain the redshift via Cosmology_getRedshift, and use the
previous relation to obtain the scaling factor. The time represented by a
cosmological redshift can be obtained by a call to
Cosmology_redshiftToTime and passing it a cosmological redshift.
Note also that if a collisionless matter component (e.g.particles)
is also present, its density must be added to the gas density on the
right-hand side of (22.7). Accounting for particle masses in density
is handled by the Gravity unit.
The comoving mean matter density is defined in terms of the critical
density
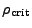 by
by
The Hubble parameter 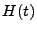 [to be distinguished from the Hubble “constant”
[to be distinguished from the Hubble “constant”
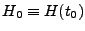 ] is given by the Friedman equation
] is given by the Friedman equation
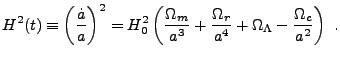 |
(22.9) |
Here 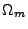 ,
, 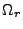 , and
, and
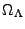 are the present-day
densities, respectively, of matter, radiation, and cosmological constant,
divided by
are the present-day
densities, respectively, of matter, radiation, and cosmological constant,
divided by
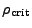 . The contribution of the overall spatial
curvature of the universe is given by
. The contribution of the overall spatial
curvature of the universe is given by
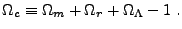 |
(22.10) |
The Cosmology_solveFriedmannEqn routine numerically solves the Friedmann
equation to obtain
the scale factor and its rate of change as functions of time.
In principle, any good ODE integrator can be used; the csm_integrateFriedman
subroutine uses a fourth-order Runge-Kutta method to integrate the
Friedmann equation under the assumption that
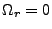 . Subunits
can also use analytic solutions where appropriate.
. Subunits
can also use analytic solutions where appropriate.
Redshift terms for particles are handled separately by the appropriate
time integration subunits of the Particles unit. For an example,
see the LeapfrogCosmo implementation of the ParticlesMain subunit
in Sec:Active Partices Integration.
![]() , where
, where ![]() is a proper position
vector and
is a proper position
vector and ![]() is the time-dependent cosmological scale factor.
The present epoch is defined to correspond to
is the time-dependent cosmological scale factor.
The present epoch is defined to correspond to ![]() ; in the following
discussion we use
; in the following
discussion we use ![]() to refer to the age of the Universe at the
present epoch.
The gas velocity
to refer to the age of the Universe at the
present epoch.
The gas velocity ![]() is taken to be the comoving peculiar
velocity
is taken to be the comoving peculiar
velocity
![]() . The comoving gas density, pressure, temperature,
and internal energy are defined to be
. The comoving gas density, pressure, temperature,
and internal energy are defined to be
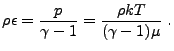
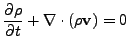
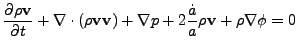
![$\displaystyle {\partial\rho E\over\partial t} + \nabla\cdot[(\rho E + p){\bf v}...
...}\over a}[(3\gamma-1)\rho\epsilon + 2\rho v^2] + \rho{\bf v}\cdot\nabla\phi = 0$](img2348.png)
![$\displaystyle {\partial\rho\epsilon\over\partial t} + \nabla\cdot[(\rho\epsilon...
...\bf v}] -{\bf v}\cdot\nabla p + {{\dot a}\over a}(3\gamma-1)\rho\epsilon = 0 .$](img2349.png)
![]() in the above equations
is the solution to the Poisson equation in the form
in the above equations
is the solution to the Poisson equation in the form
![]() (
(
![]() ),
can obtain the redshift via Cosmology_getRedshift, and use the
previous relation to obtain the scaling factor. The time represented by a
cosmological redshift can be obtained by a call to
Cosmology_redshiftToTime and passing it a cosmological redshift.
Note also that if a collisionless matter component (e.g.particles)
is also present, its density must be added to the gas density on the
right-hand side of (22.7). Accounting for particle masses in density
is handled by the Gravity unit.
),
can obtain the redshift via Cosmology_getRedshift, and use the
previous relation to obtain the scaling factor. The time represented by a
cosmological redshift can be obtained by a call to
Cosmology_redshiftToTime and passing it a cosmological redshift.
Note also that if a collisionless matter component (e.g.particles)
is also present, its density must be added to the gas density on the
right-hand side of (22.7). Accounting for particle masses in density
is handled by the Gravity unit.
![]() by
by