Next: 21.2 Mesh/Particle Mapping Up: 21. Particles Unit Previous: 21. Particles Unit Contents Index
The active and passive particles have many different time integration schemes available. The subroutine Particles_advance handles the movement of particles through space and time. Because FLASH4 has support for including different types of both active and passive particles in a single simulation, the implementation of Particles_advance may call several helper routines of the form pt_advanceMETHOD (e.g., pt_advanceLeapfrog, pt_advanceEuler_active, pt_advanceCustom), each acting on an appropriate subset of existing particles. The METHOD here is determined by the ADVMETHOD part of the PARTICLETYPE Config statement (or the ADV par of a -particlemethods setup option) for the type of particle. See the Particles_advance source code for the mapping from ADVMETHOD keyword to pt_advanceMETHOD subroutine call.
The active particles implementation includes different time integration schemes, long-range force laws (coupling all particles), and short-range force laws (coupling nearby particles). The attributes listed in Table 21.1 are provided by this subunit. A specific implementation of the active portion of Particles_advance is selected by a setup option such as -with-unit=Particles/ParticlesMain/active/massive/Leapfrog, or by specifying something like REQUIRES Particles/ParticlesMain/active/massive/Leapfrog in a simulation's Config file (or by listing the path in the Units file if not using the -auto configuration option). Further details are given is Sec:ParticlesUsing below.
Available time integration schemes for active particles include
| (21.4) |
| (21.5) | |||
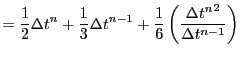 |
|||
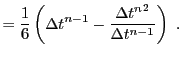 |
(21.6) |
![$\displaystyle {\bf v}_i^{n-1/2}
\left[ 1 - {A^n\over 2} \Delta t^n
+ {1\over 3!...
...{A^n\over 2}
+ {\Delta t^{n-1}}^2 {{A^n}^2+
2\dot A^n\over 12} \right]\nonumber$](img2161.png) |
|||
![$\displaystyle + {\bf a}_i^n \left[ {\Delta t^{n-1}\over 2} +
{{\Delta t^n}^2\ov...
...
- { A^n \Delta t^n \over 6}
\left( \Delta t^n + \Delta t^{n-1} \right)
\right]$](img2162.png) |
|||
![$\displaystyle + {\bf a}_i^{n-1} \left[ {{\Delta t^{n-1}}^2 - {\Delta t^n}^2
\ov...
...t^{n-1}}
- { A^n \Delta t^{n-1} \over 12}
(\Delta t^n + \Delta t^{n-1}) \right]$](img2163.png) |
|||
The leapfrog-based integrators implemented under Particles/ParticlesMain/active/massive supply the additional particle attributes listed in Table 21.2.
Collisionless plasmas are often modeled using fluid magnetohydrodynamics (MHD) models. However, the MHD fluid approximation is questionable when the gyroradius of the ions is large compared to the spatial region that is studied. On the other hand, kinetic models that discretize the full velocity space, or full particle in cell (PIC) models that treat ions and electrons as particles, are computationally very expensive. For problems where the time scales and spatial scales of the ions are of interest, hybrid models provide a compromise. In such models, the ions are treated as discrete particles, while the electrons are treated as a (often massless) fluid. This mean that the time scales and spatial scales of the electrons do not need to be resolved, and enables applications such as modeling of the solar wind interaction with planets. For a detailed discussion of different plasma models, see Ledvina et al. (2008).
The trajectories of the ions are computed from the Lorentz force,
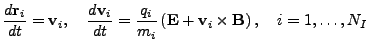
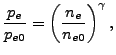
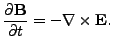
The equations are stated in SI units, so all parameters
should be given in SI units, and all output will be in SI units.
The initial configuration is a spatial uniform plasma consisting of
two species. The first species, named pt_picPname_1
consists of particles of mass pt_picPmass_1 and charge
pt_picPcharge_1.
The initial (at ![]() ) uniform number density is pt_picPdensity_1,
and the velocity distribution is Maxwellian with a drift velocity of
(pt_picPvelx_1, pt_picPvely_1, pt_picPvelz_1),
and a temperature of pt_picPtemp_1.
Each model macro-particle represents many real particles.
The number of macro-particles per grid cell at the start of the simulation
is set by pt_picPpc_1.
So this parameter will control the total number of macro-particles
of species 1 in the simulation.
) uniform number density is pt_picPdensity_1,
and the velocity distribution is Maxwellian with a drift velocity of
(pt_picPvelx_1, pt_picPvely_1, pt_picPvelz_1),
and a temperature of pt_picPtemp_1.
Each model macro-particle represents many real particles.
The number of macro-particles per grid cell at the start of the simulation
is set by pt_picPpc_1.
So this parameter will control the total number of macro-particles
of species 1 in the simulation.
All the above parameters are also available for a second species, e.g.,
pt_picPmass_2,
which is initialized in the same way as the first species.
| Variable | Type | Default | Description |
| pt_picPname_1 | STRING | "H+" | Species 1 name |
| pt_picPmass_1 | REAL | 1.0 | Species 1 mass, |
| pt_picPcharge_1 | REAL | 1.0 | Species 1 charge, |
| pt_picPdensity_1 | REAL | 1.0 | Initial |
| pt_picPtemp_1 | REAL | 1.5e5 | Initial |
| pt_picPvelx_1 | REAL | 0.0 | Initial
|
| pt_picPvely_1 | REAL | 0.0 | |
| pt_picPvelz_1 | REAL | 0.0 | |
| pt_picPpc_1 | REAL | 1.0 | Number of macro-particle of species 1 per cell |
| sim_bx | REAL | 0.0 | Initial
|
| sim_by | REAL | 0.0 | |
| sim_bz | REAL | 0.0 | |
| sim_te | REAL | 0.0 | Initial |
| pt_picResistivity | REAL | 0.0 | Resistivity, |
| pt_picResistivityHyper | REAL | 0.0 | Hyperresistivity, |
| sim_gam | REAL | -1.0 | Adiabatic exponent for electrons |
| sim_nsub | INTEGER | 3 | Number of CL B-field update subcycles (must be odd) |
| sim_rng_seed | INTEGER | 0 | Seed the random number generator (if |
Now for grid quantities.
The cell averaged mass density is stored in pden, and the
charge density in cden.
The magnetic field is represented by
(grbx, grby, grbz).
A background field can be set during initialization in
(gbx1, gby1, gbz1).
We then solve for the deviation from this background field.
Care must be take so that the background field is divergence free,
using the discrete divergence operator.
The easiest way to ensure this is to compute the background field
as the rotation of a potential.
The electric field is stored in
(grex, grey, grez), the current density in
(grjx, grjy, grjz) , and the ion current density in
(gjix, gjiy, gjiz).
A resistivity is stored in gres, thus it is possible to have
a non-uniform resistivity in the simulation domain, but the default
is to set the resistivity to the constant value of sim_resistivity
everywhere. For post processing, separate fields are stored for
charge density and ion current density for species 1 and 2.
| Variable | Type | Description |
| cden | PER_VOLUME | Total charge density, |
| grbx | GENERIC | Magnetic field,
|
| grby | GENERIC | |
| grbz | GENERIC | |
| grex | GENERIC | Electric field,
|
| grey | GENERIC | |
| grez | GENERIC | |
| grjx | PER_VOLUME | Current density,
|
| grjy | PER_VOLUME | |
| grjz | PER_VOLUME | |
| gjix | PER_VOLUME | Ion current density,
|
| gjiy | PER_VOLUME | |
| gjiz | PER_VOLUME | |
| cde1 | PER_VOLUME | Species 1 charge density, |
| jix1 | PER_VOLUME | Species 1 ion current density,
|
| jiy1 | PER_VOLUME | |
| jiz1 | PER_VOLUME |
Regarding particle properties.
Each computational meta-particles is labeled by a positive integer,
specie and has a mass and charge.
As all FLASH particles they also each have a
position
![]() =(posx, posy, posz)
and a velocity
=(posx, posy, posz)
and a velocity
![]() =(velx, vely, velz).
To be able to deposit currents onto the grid, each particle stores
the current density corresponding to the particle,
=(velx, vely, velz).
To be able to deposit currents onto the grid, each particle stores
the current density corresponding to the particle,
![]() .
For the movement of the particles by the Lorentz force, we also need
the electric and magnetic fields at the particle positions,
.
For the movement of the particles by the Lorentz force, we also need
the electric and magnetic fields at the particle positions,
![]() and
and
![]() , respectivly.
, respectivly.
| Variable | Type | Description |
| specie | REAL | Particle type (an integer number 1,2,3,...) |
| mass | REAL | Mass of the particle, |
| charge | REAL | Charge of the particle, |
| jx | REAL | Particle ion current,
|
| jy | REAL | |
| jz | REAL | |
| bx | REAL | Magnetic field at particle,
|
| by | REAL | |
| bz | REAL | |
| ex | REAL | Electric field at particle,
|
| ey | REAL | |
| ez | REAL |
Regarding the choice of time step.
The timestep must be constant, ![]() dtinit = dtmin = dtmax,
since the leap frog solver requires this.
For the solution to be stable
the time step,
dtinit = dtmin = dtmax,
since the leap frog solver requires this.
For the solution to be stable
the time step, ![]() , must be small enough.
We will try and quantify this, and here we asume that the grid
cells are cubes,
, must be small enough.
We will try and quantify this, and here we asume that the grid
cells are cubes,
![]() , and that we have
a single species plasma.
, and that we have
a single species plasma.
First of all, since the time advancement is explicit,
there is the standard CFL condition that no particle should travel
more than one grid cell in one time step, i.e.
![]() max
max![]() .
This time step is printed to standard output by FLASH (as dt_Part),
and can thus be monitored.
.
This time step is printed to standard output by FLASH (as dt_Part),
and can thus be monitored.
Secondly, we also have an upper limit on the time step due to Whistler waves (Pritchett 2000),
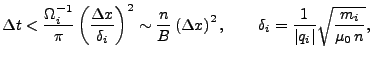
Finally, we also want to resolve the ion gyro motion by having several
time steps per gyration. This will only put a limit on the time step
if, approximately,
![]() , and we then
have that
, and we then
have that
![]() .
.
All this are only estimates that does not take into account, e.g.,
the initial functions, or the subcycling of the magnetic field update.
In practice one can just reduce the time step until the solution is stable.
Then for runs with different density and/or magnetic field strength,
the time step will need to be scaled by the change in ![]() ,
e.g., if
,
e.g., if ![]() is doubled,
is doubled, ![]() can be doubled.
The factor
can be doubled.
The factor
![]() implies that reducing the cell
size by a factor of two will require a reduction in the time step by
a factor of four.
implies that reducing the cell
size by a factor of two will require a reduction in the time step by
a factor of four.
Numerically solving Equation (21.1) for passive particles
means solving a set of simple ODE initial value problems, separately for each particle,
where the velocities ![]() are given at certain discrete points in time
by the state of the hydrodynamic velocity field at those times.
The time step is thus externally given and cannot be arbitrarily chosen by
a particle motion ODE solver21.1. Statements about the order of a method in this context should
be understood as referring to the same method if it were applied in a hypothetical
simulation where evaluations of velocities
are given at certain discrete points in time
by the state of the hydrodynamic velocity field at those times.
The time step is thus externally given and cannot be arbitrarily chosen by
a particle motion ODE solver21.1. Statements about the order of a method in this context should
be understood as referring to the same method if it were applied in a hypothetical
simulation where evaluations of velocities ![]() could be performed at
arbitrary times (and with unlimited accuracy). Note that FLASH4 does not
attempt to provide a particle motion ODE solver of higher accuracy than second order,
since it makes little sense to integrate particle motion to a higher order
than the fluid dynamics that provide its inputs.
could be performed at
arbitrary times (and with unlimited accuracy). Note that FLASH4 does not
attempt to provide a particle motion ODE solver of higher accuracy than second order,
since it makes little sense to integrate particle motion to a higher order
than the fluid dynamics that provide its inputs.
In all cases, particles are advanced in time from ![]() (or, in the
case of Midpoint, from
(or, in the
case of Midpoint, from ![]() ) to
) to
![]() using one of the difference equations described below. The
implementations assume that at the time when
Particles_advance is called, the fluid fields have
already been updated to
using one of the difference equations described below. The
implementations assume that at the time when
Particles_advance is called, the fluid fields have
already been updated to ![]() , as is the case with the
Driver_evolveFlash implementations provided with
FLASH4. A specific implementation of the passive portion of
Particles_advance
is selected by a setup option such
as -with-unit=Particles/ParticlesMain/passive/Euler, or by
specifying something like REQUIRES
Particles/ParticlesMain/passive/Euler in a simulation's
Config file (or by listing the path in the Units file if
not using the -auto configuration option).
Further details are given is Sec:ParticlesUsing below.
, as is the case with the
Driver_evolveFlash implementations provided with
FLASH4. A specific implementation of the passive portion of
Particles_advance
is selected by a setup option such
as -with-unit=Particles/ParticlesMain/passive/Euler, or by
specifying something like REQUIRES
Particles/ParticlesMain/passive/Euler in a simulation's
Config file (or by listing the path in the Units file if
not using the -auto configuration option).
Further details are given is Sec:ParticlesUsing below.
Note that this evaluation of
![]() cannot be deferred until the time when it is
needed at
cannot be deferred until the time when it is
needed at ![]() , since at that point the fluid variables have been updated
and the velocity fields at
, since at that point the fluid variables have been updated
and the velocity fields at ![]() are not available any more. Particle velocities are therefore
interpolated from the mesh at
are not available any more. Particle velocities are therefore
interpolated from the mesh at ![]() and stored as particle attributes.
Similar concerns apply to the remaining methods but will not be explicitly mentioned
every time.
and stored as particle attributes.
Similar concerns apply to the remaining methods but will not be explicitly mentioned
every time.
| (21.9) |
To get the scheme started, an Euler step (as described for passive/Euler) is taken the first time Particles/ParticlesMain/passive/Midpoint/pt_advancePassive is called.
The Midpoint alternative implementation uses the following additional particle attributes:
PARTICLEPROP pos2PrevX REAL # two previous x-coordinate PARTICLEPROP pos2PrevY REAL # two previous y-coordinate PARTICLEPROP pos2PrevZ REAL # two previous z-coordinate
Particle advancement follows the equation
Conditions for the correction can be derived as follows:
Let
![]() the estimated half time step
used in the scheme, let
the estimated half time step
used in the scheme, let
![]() the estimated midpoint time,
and
the estimated midpoint time,
and
![]() the actual midpoint of the
the actual midpoint of the
![]() interval.
Also write
interval.
Also write
![]() for
first-order (Euler) approximate positions
at the actual midpoint time
for
first-order (Euler) approximate positions
at the actual midpoint time
![]() ,
and we continue to denote with
,
and we continue to denote with
![]() the estimated positions
reached at the estimated mipoint time
the estimated positions
reached at the estimated mipoint time
![]() .
.
Assuming reasonably smooth functions
![]() ,
we can then write
for the exact value of the velocity field at the approximate
positions
evaluated at the actual midpoint time
,
we can then write
for the exact value of the velocity field at the approximate
positions
evaluated at the actual midpoint time
On the other hand, expansion of (21.11) gives
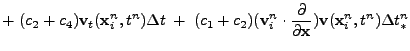 |
|||
One can derive conditions for second order accuracy by comparing (21.13) with (21.12) and requiring that
| (21.14) |
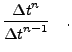 |
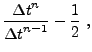 |
|||
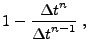 |
|||
An Euler step, as described for passive/Euler in (21.7), is taken the first time when Particles/ParticlesMain/passive/EstiMidpoint2/pt_advancePassive is called and when the time step has changed too much. Since the integration scheme is tolerant of time step changes, it should usually not be necessary to apply the second criterion; even when it is to be employed, the criteria should be less strict than for an uncorrected EstiMidpoint scheme. For EstiMidPoint2 the timestep is considered to have changed too much if either of the following is true:
The EstiMidpoint2 alternative implementation uses the following additional particle attributes
for storing the values of
![]() and
and
![]() between the Particles_advance calls at
between the Particles_advance calls at ![]() and
and ![]() :
:
PARTICLEPROP velPredX REAL PARTICLEPROP velPredY REAL PARTICLEPROP velPredZ REAL PARTICLEPROP posPredX REAL PARTICLEPROP posPredY REAL PARTICLEPROP posPredZ REAL
The time integration of passive particles is tested in the ParticlesAdvance unit test, which can be used to examine the convergence behavior, see Sec:ParticlesUnitTest.