Next: 22. Cosmology Unit Up: 21. Particles Unit Previous: 21.3 Using the Particles Contents Index
Sink particles are required in collapse simulations to model dense core, star, or black hole formation and accretion. Using sink particles solves two main problems in collapse calculations:
To include sink particles, specify REQUIRES Particles/ParticlesMain/active/Sink in the simulation Config file. This automatically includes all required subunits for the sink particles. Currently, sink particles require a Paramesh 4 Grid implementation and Poisson gravity. Currently, various subunits and implementation directories of the Particles unit and are also included automatically. Table 21.6 lists all runtime parameters of the sink particle module. The default values of these parameters should be ok in most simulations, except sink_density_thresh, sink_accretion_radius, and sink_softening_radius. Those three parameters have to be adopted to the resolution and physics of a given simulation.
First, the sink particle accretion radius,
![]() (sink_accretion_radius) should be calculated, based on the minimum cell size
(sink_accretion_radius) should be calculated, based on the minimum cell size ![]() for a given simulation. The recommended value is
for a given simulation. The recommended value is
![]() . If sink particles are included, the code will print a message to the standard output, stating the number of cells that a chosen sink accretion radius corresponds to. The recommended value for the sink particle softening radius (sink_softening_radius) is to set it equal to the accretion radius.
. If sink particles are included, the code will print a message to the standard output, stating the number of cells that a chosen sink accretion radius corresponds to. The recommended value for the sink particle softening radius (sink_softening_radius) is to set it equal to the accretion radius.
In order to avoid artificial fragmentation, the gas density on the AMR grid must not exceed a critical density
![]() in regions of gravitational collapse (Truelove et al. 1997). This density is related to the smallest resolvable Jeans length
in regions of gravitational collapse (Truelove et al. 1997). This density is related to the smallest resolvable Jeans length
![]() on the highest level of the AMR hierarchy. The density threshold
on the highest level of the AMR hierarchy. The density threshold
![]() (sink_density_thresh) is obtained by solving the definition of the Jeans length, Equation (21.31) for
(sink_density_thresh) is obtained by solving the definition of the Jeans length, Equation (21.31) for ![]() ,
,
Please cite Federrath et al. (2010, ApJ 713, 269) if you are using this unit.
| Variable | Type | Default | Description |
| useSinkParticles | BOOLEAN | .false. | switch sinks on/off |
| sink_density_thresh | REAL | 1.0e-14 | density threshold for sink creation and accretion |
| sink_accretion_radius | REAL | 1.0e14 | creation and accretion radius |
| sink_softening_radius | REAL | 1.0e14 | gravitational softening radius |
| sink_softening_type_gas | STRING | "linear" | sink-gas softening type (options: "linear", "spline") |
| sink_softening_type_sinks | STRING | "spline" | sink-sink softening type (options: "linear", "spline") |
| sink_integrator | STRING | "leapfrog" | sink particle time integrator (options: "euler", "leapfrog", "leapfrog_cosmo") |
| sink_dt_factor | REAL | 0.5 | time step safety factor ( |
| sink_subdt_factor | REAL | 0.01 | time step safety factor for sink-sink subcycling ( |
| sink_convergingFlowCheck | BOOLEAN | .true. | creation check for converging gas flow |
| sink_potentialMinCheck | BOOLEAN | .true. | creation check for gravitational potential minimum |
| sink_jeansCheck | BOOLEAN | .true. | creation check for Jeans instability |
| sink_negativeEtotCheck | BOOLEAN | .true. | creation check for gravitationally bound gas |
| sink_GasAccretionChecks | BOOLEAN | .true. | check for bound and converging state before gas accretion |
| sink_merging | BOOLEAN | .false. | switch for sink particle merging |
| sink_offDomainSupport | BOOLEAN | .false. | support for sink particles to remain active when leaving the grid domain (in case of outflow boundary conditions) |
| sink_AdvanceSerialComputation | BOOLEAN | .true. | use the global sink particle array for time advancement (to greatly speed up computation of sink-sink interaction) |
| pt_maxSinksPerProc | INTEGER | 100 | number of sinks per processor |
| refineOnSinkParticles | BOOLEAN | .true. | sinks must be on highest AMR level |
| refineOnJeansLength | BOOLEAN | .true. | switch for refinement on Jeans length |
| jeans_ncells_ref | REAL | 32.0 | number of cells for Jeans length refinement |
| jeans_ncells_deref | REAL | 64.0 | number of cells for Jeans length de-refinement |
For technical details and tests of the FLASH sink particle unit, see Federrath et al. (2010, ApJ 713, 269) and Federrath et al. (2011, IAUS 270, 425). We only summarize here the most important aspects of the implementation.
Before a sink particle is created, we define a spherical control volume with the accretion radius
![]() around each cell that exceeds the resolution-dependent density threshold,
around each cell that exceeds the resolution-dependent density threshold,
![]() given by Equation (21.32), and check whether the gas in this control volume
given by Equation (21.32), and check whether the gas in this control volume
We take all contributions to the gravitational interactions between the gas on the grid and the sink particles into account. Those interactions are
To invoke the sink particle unit test, use ./setup unitTest/SinkMomTest -auto -3d. This initializes a momentum conservation test. An initially uniform cloud with radius
![]() and density
and density
![]() at rest starts collapsing and forms a sink particle. An initial sink particle with
at rest starts collapsing and forms a sink particle. An initial sink particle with
![]() and initial momentum
and initial momentum
![]() in positive
in positive ![]() -direction is also present. The purpose of this test is to see how well the total
-direction is also present. The purpose of this test is to see how well the total ![]() -momentum
-momentum ![]() and the total
and the total ![]() -momentum
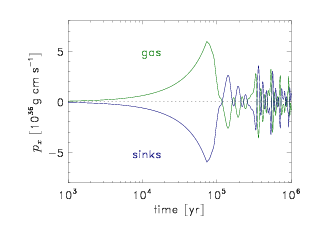
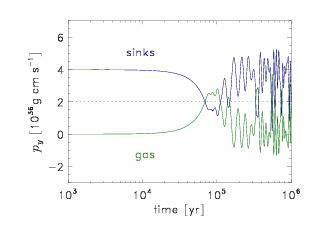
-momentum ![]() are conserved. This test is particularly suitable, because it involves gas collapse, sink particle creation, accretion, more than one sink particle, and thus all gravitational interactions (gas-gas, gas-sinks, sinks-gas, sinks-sinks), as well as close eccentric orbits of the two sink particles. Figure 21.3 shows
are conserved. This test is particularly suitable, because it involves gas collapse, sink particle creation, accretion, more than one sink particle, and thus all gravitational interactions (gas-gas, gas-sinks, sinks-gas, sinks-sinks), as well as close eccentric orbits of the two sink particles. Figure 21.3 shows ![]() and
and ![]() as a function of time for both sink particles and gas separately. The symmetry between sink and gas momenta shows that momentum is well conserved for several orbits. Figure 21.3 can be reproduced with the IDL and Python tools in /source/Simulation/SimulationMain/unitTest/SinkMomTest/utils/ by running the IDL script plot_mom_sinks.pro.
as a function of time for both sink particles and gas separately. The symmetry between sink and gas momenta shows that momentum is well conserved for several orbits. Figure 21.3 can be reproduced with the IDL and Python tools in /source/Simulation/SimulationMain/unitTest/SinkMomTest/utils/ by running the IDL script plot_mom_sinks.pro.
|