Subsections
21.2 Mesh/Particle Mapping
Particles behave in a fundamentally different way than grid-based quantities.
Lagrangian, or passive particles are essentially independent of the grid mesh and move
along with the velocity field. Active particles may be located independently of mesh refinement.
In either case, there is a need to convert grid-based quantities into similar attributes defined
on particles, or vice versa.
The method for interpolating mesh quantities to tracer particle positions must
be consistent with the numerical method to avoid introducing systematic
error. In the case of a finite-volume methods such as those used in FLASH4, the mesh
quantities have cell-averaged rather than point values, which requires
that the interpolation function for the particles also represent
cell-averaged values. Cell averaged quantities are defined as
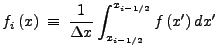 |
(21.15) |
where 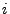 is the cell index and
is the cell index and 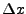 is the spatial
resolution.
The mapping back and forth from the mesh to the particle properties
are defined in the routines Particles_mapFromMesh and
Particles_mapToMeshOneBlk.
is the spatial
resolution.
The mapping back and forth from the mesh to the particle properties
are defined in the routines Particles_mapFromMesh and
Particles_mapToMeshOneBlk.
Specifying the desired mapping method is accomplished by designating the MAPMETHOD
in the Simulation Config file for each type of particle.
See Sec:FlashHparttypes for more details.
The quadratic mapping package defines an interpolation back and forth
to the mesh which is second order. This implementation is primarily
meant to be used with passive tracer particles.
To derive it, first consider a
second-order interpolation function of the form
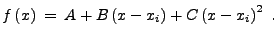 |
(21.16) |
Then integrating gives
and
We may write these as
![$\displaystyle \left[ \begin{array}{c} f_{i+1} f_{i} f_{i-1} \end{array} \...
...eft[ \begin{array}{ccc} A B\Delta x C \Delta x^2 \end{array} \right] \; .$](img2294.png) |
(21.20) |
Inverting this gives expressions for 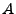 ,
, 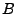 , and
, and 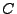 ,
,
![$\displaystyle \left[ \begin{array}{c} A B\Delta x C \Delta x^2 \end{array...
... \left[ \begin{array}{ccc} f_{i+1} f_{i} f_{i-1} \end{array} \right] \; .$](img2295.png) |
(21.21) |
In two dimensions, we want a second-order interpolation function of the form
 |
(21.22) |
In this case, the cell averaged quantities are given by
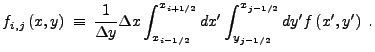 |
(21.23) |
Integrating the 9 possible cell averages gives, after some algebra,
![$\displaystyle \left[ \begin{array}{c} f_{i-1,j-1} f_{i,j-1} f_{i+1,j-1} \...
...2 D \Delta y E \Delta y^2 F \Delta x \Delta y \end{array} \right] \; .$](img2298.png) |
(21.24) |
At this point we note that there are more constraints than unknowns,
and we must make a choice of the constraints. We chose to ignore
the cross terms and take only the face-centered cells next to
the cell containing the particle, giving
![$\displaystyle \left[ \begin{array}{c} f_{i,j-1} f_{i-1,j} f_{i,j} f_{i...
...\Delta x C \Delta x^2 D \Delta y E \Delta y^2 \end{array} \right] \; .$](img2299.png) |
(21.25) |
Inverting gives
![$\displaystyle \left[ \begin{array}{c} A B\Delta x C \Delta x^2 D \Delt...
...j-1} f_{i-1,j} f_{i,j} f_{i+1,j} f_{i,j+1} \end{array} \right] \; .$](img2300.png) |
(21.26) |
Similarly, in three dimensions, the interpolation function is
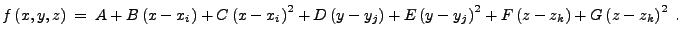 |
(21.27) |
and we have
![$\displaystyle \left[ \begin{array}{c} A B \Delta x C {\Delta x}^2 D \D...
...f_{i,j,k} f_{i+1,j,k} f_{i,j+1,k} f_{i,j,k+1} \end{array} \right] \; .$](img2302.png) |
(21.28) |
Finally, the above expressions apply only to Cartesian coordinates. In the case of
cylindrical
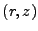 coordinates, we have
coordinates, we have
and
![$\displaystyle \left[ \begin{array}{c}
A B\Delta r C\Delta r^{\frac{2}{6}} D\Delta z E \Delta z^2
\end{array} \right] \: = \hspace{-1.0in}$](img2307.png) |
|
|
|
| |
![$\displaystyle \left[ \begin{array}{cccccc}
-\frac{1}{24} & -\frac{h_1-1}{24h_1}...
...-1} f_{i-1,j} f_{i,j} \\
f_{i+1,j} f_{i,j+1}
\end{array} \right] \; .$](img2308.png) |
|
(21.30) |
21.2.2 Cloud in Cell Mapping
Other interpolation routines can be defined that take into account
the actual quantities defined on the grid. These “mesh-based”
algorithms are represented in FLASH4 by the Cloud-in-Cell
mapping, where the interpolation to/from the particles is defined
as a simple linear weighting from nearby grid points. The weights are
defined by considering only the region of one “cell” size around
each particle location; the proportional volume of the particle
“cloud” corresponds to the amount allocated to/from the mesh. The
CIC method can be used with both types of particles. When using it
with active particles the MapToMesh methods should also be
selected. In order to include the CIC method with passive particles,
the setup command line option is
-with-unit=Particles/ParticlesMapping/CIC. Two additional
command line option
-with-unit=Particles/ParticlesMapping/MapToMesh and
-with-unit=Grid/GridParticles/MapToMesh are necessary
when using the active particles. All of these command line options can
be replaced by placing the appropriate REQUIRES/REQUESTS
directives in the Simulation Config file.
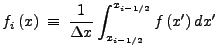
![$\displaystyle \: \frac{1}{\Delta x}\left[ A + \left. \frac{1}{2}
B \left(x - x_...
...frac{1}{3}
C \left(x - x_i\right)^3 \right\vert^{x_{i-1/2}}_{x_{i-3/2}} \right]$](img2288.png)
![$\displaystyle \: \frac{1}{\Delta x}\left[ A + \left. \frac{1}{2} B \left(x - x_...
...frac{1}{3} C \left(x - x_i\right)^3 \right\vert^{x_{i+1/2}}_{x_{i-1/2}} \right]$](img2291.png)
![$\displaystyle \: \frac{1}{\Delta x}\left[ A + \left. \frac{1}{2}
B \left(x - x_...
...frac{1}{3}
C \left(x - x_i\right)^3 \right\vert^{x_{i-1/2}}_{x_{i-3/2}} \right]$](img2288.png)
![$\displaystyle \left[ \begin{array}{c} f_{i+1} f_{i} f_{i-1} \end{array} \...
...eft[ \begin{array}{ccc} A B\Delta x C \Delta x^2 \end{array} \right] \; .$](img2294.png)
![$\displaystyle \left[ \begin{array}{c} A B\Delta x C \Delta x^2 \end{array...
... \left[ \begin{array}{ccc} f_{i+1} f_{i} f_{i-1} \end{array} \right] \; .$](img2295.png)
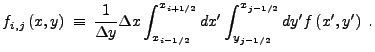
![$\displaystyle \left[ \begin{array}{c} f_{i-1,j-1} f_{i,j-1} f_{i+1,j-1} \...
...2 D \Delta y E \Delta y^2 F \Delta x \Delta y \end{array} \right] \; .$](img2298.png)
![$\displaystyle \left[ \begin{array}{c} f_{i,j-1} f_{i-1,j} f_{i,j} f_{i...
...\Delta x C \Delta x^2 D \Delta y E \Delta y^2 \end{array} \right] \; .$](img2299.png)
![$\displaystyle \left[ \begin{array}{c} A B\Delta x C \Delta x^2 D \Delt...
...j-1} f_{i-1,j} f_{i,j} f_{i+1,j} f_{i,j+1} \end{array} \right] \; .$](img2300.png)
![$\displaystyle \left[ \begin{array}{c} A B \Delta x C {\Delta x}^2 D \D...
...f_{i,j,k} f_{i+1,j,k} f_{i,j+1,k} f_{i,j,k+1} \end{array} \right] \; .$](img2302.png)
![$\displaystyle \left[ \begin{array}{c}
A B\Delta r C\Delta r^{\frac{2}{6}} D\Delta z E \Delta z^2
\end{array} \right] \: = \hspace{-1.0in}$](img2307.png)
![$\displaystyle \left[ \begin{array}{cccccc}
-\frac{1}{24} & -\frac{h_1-1}{24h_1}...
...-1} f_{i-1,j} f_{i,j} \\
f_{i+1,j} f_{i,j+1}
\end{array} \right] \; .$](img2308.png)