Here we solve
where 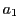 and
and 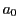 are real. Well known techniques (larger magnitude root
are real. Well known techniques (larger magnitude root 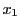 computed by quadratic formula, smaller magnitude root computed by applying Vieta's rule:
computed by quadratic formula, smaller magnitude root computed by applying Vieta's rule:
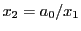 ) are used to ensure numerical accuracy of the roots. Additionally the
code is equipped to deal with extremely large coefficients, such that computational
overflow will not occur. A coefficient rescaling technique is applied if during evaluation
of the quadratic formula either the term
) are used to ensure numerical accuracy of the roots. Additionally the
code is equipped to deal with extremely large coefficients, such that computational
overflow will not occur. A coefficient rescaling technique is applied if during evaluation
of the quadratic formula either the term  or the discriminant
or the discriminant
 become larger than the largest positive number on the machine.
become larger than the largest positive number on the machine.