This solves the cubic polynomial equation
where 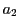 ,
,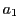 and
and 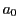 are real. Rather than calculating the roots by the analytical
formulas, a special technique has been devised to pinpoint down one of the real roots
by iteration. After rescaling the cubic polynomial coefficients such that
are real. Rather than calculating the roots by the analytical
formulas, a special technique has been devised to pinpoint down one of the real roots
by iteration. After rescaling the cubic polynomial coefficients such that
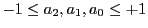 and classifying the rescaled cubic polynomials into 6 classes,
an analysis of the real root(s) surfaces for each class enables one to find an optimum
starting point for a fast convergent Newton-Raphson iteration. In rare cases when the
Newton-Raphson iterations start oscillating around the root due to numerical rounding errors,
a bisection iteration follows to get the root to within machine accuracy. Details of this
procedure can be found in Flocke 2015. After one of the real roots has been found, the remaining
roots (real or complex) are found by solving the residual quadratic, which is obtained by composite
(forward/backward) deflation.
and classifying the rescaled cubic polynomials into 6 classes,
an analysis of the real root(s) surfaces for each class enables one to find an optimum
starting point for a fast convergent Newton-Raphson iteration. In rare cases when the
Newton-Raphson iterations start oscillating around the root due to numerical rounding errors,
a bisection iteration follows to get the root to within machine accuracy. Details of this
procedure can be found in Flocke 2015. After one of the real roots has been found, the remaining
roots (real or complex) are found by solving the residual quadratic, which is obtained by composite
(forward/backward) deflation.