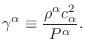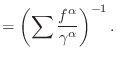17.5 MultiFluid
The multiFluid implementation of the equation of state is meant to complement the volume-of-fluid (VOF) hydrodynamics solver for capturing material interfaces described in sec:vof. The EoS operates as previously described for any cells that are purely a single fluid. In mixed cells the EoS is called separately on each of the components, here labelled by  , for the state
, for the state
 . After a call to the EoS it is possible that
. After a call to the EoS it is possible that
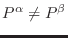 . In order to maintain the mechanical equilibrium assumed in VOF the volume fractions,
. In order to maintain the mechanical equilibrium assumed in VOF the volume fractions, 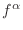 need to be relaxed until the two pressures equilibriate. First an average pressure is computed,
need to be relaxed until the two pressures equilibriate. First an average pressure is computed,
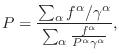 |
(17.27) |
and the component fluid states are adjusted as
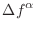 |
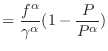 |
(17.28) |
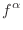 |
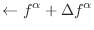 |
(17.29) |
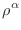 |
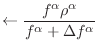 |
(17.30) |
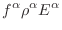 |
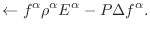 |
(17.31) |
In the above
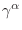 is the adiabatic index for fluid
is the adiabatic index for fluid 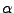 as in other EoS implementations,
as in other EoS implementations,
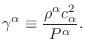 |
(17.32) |
An equivalent single fluid state may also be parameterized in mixed cells as
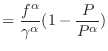
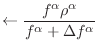
![]() is the adiabatic index for fluid
is the adiabatic index for fluid ![]() as in other EoS implementations,
as in other EoS implementations,