15.1 Gas hydrodynamics

15.1.1 Usage

The two gas hydrodynamic solvers supplied in the release of FLASH4 are organized into two different operator splitting methods: directionally split and unsplit. The directionally split piecewise-parabolic method (PPM) makes use of second-order Strang time splitting, and the new directionally unsplit solver is based on Monotone Upstream-centered Scheme for Conservation Laws (MUSCL) Hancock type second-order scheme.

The algorithms are described in Sec:PPM and Sec:MUSCL-Hancock and implemented in the directory tree under physics/Hydro/HydroMain/split/PPM and physics/Hydro/HydroMain/unsplit/Hydro_Unsplit. Extensions for multitemperature applications are described in Sec:3THydro.

Current and future implementations of Hydro use the runtime parameters and solution variables described in Table 15.1 and Table 15.2. Additional runtime parameters used either solely by the PPM method or the unsplit hydro solver are described in HydroMain.

Table 15.1: Runtime parameters used with the hydrodynamics (Hydro) unit.

Variable	Type	Default	Description
eintSwitch	real	0	If $\epsilon < {\tt eintSwitch} \cdot {1\over 2}\vert{\bf v}\vert^2$, use the internal energy equation to update the pressure
irenorm	integer	0	If equal to one, renormalize multifluid abundances following a hydro update; else restrict their values to lie between smallx and 1.
cfl	real	0.8	Courant-Friedrichs-Lewy (CFL) factor; must be less than 1 for stability in explicit schemes

Table 15.2: Solution variables used with the hydrodynamics (Hydro) unit.

Variable	Type	Description
dens	PER_VOLUME	density
velx	PER_MASS	$x$-component of velocity
vely	PER_MASS	$y$-component of velocity
velz	PER_MASS	$z$-component of velocity
pres	GENERIC	pressure
ener	PER_MASS	specific total energy ($T+U$)
temp	GENERIC	temperature

15.1.2 The piecewise-parabolic method (PPM)

FLASH includes a directionally split piecewise-parabolic method (PPM) solver descended from the PROMETHEUS code (Fryxell, Müller, and Arnett 1989). The basic PPM algorithm is described in detail in Woodward and Colella (1984) and Colella and Woodward (1984). It is a higher-order version of the method developed by Godunov (1959). FLASH implements the Direct Eulerian version of PPM.

Godunov's method uses a finite-volume spatial discretization of the Euler equations together with an explicit forward time difference. Time-advanced fluxes at cell boundaries are computed using the numerical solution to Riemann's shock tube problem at each boundary. Initial conditions for each Riemann problem are determined by assuming the non-advanced solution to be piecewise-constant in each cell. Using the Riemann solution has the effect of introducing explicit nonlinearity into the difference equations and permits the calculation of sharp shock fronts and contact discontinuities without introducing significant nonphysical oscillations into the flow. Since the value of each variable in each cell is assumed to be constant, Godunov's method is limited to first-order accuracy in both space and time.

PPM improves on Godunov's method by representing the flow variables with piecewise-parabolic functions. It also uses a monotonicity constraint rather than artificial viscosity to control oscillations near discontinuities, a feature shared with the MUSCL scheme of van Leer (1979). Although these choices could lead to a method which is accurate to third order, PPM is formally accurate only to second order in both space and time, as a fully third-order scheme proved not to be cost-effective. Nevertheless, PPM is considerably more accurate and efficient than most formally second-order algorithms.

PPM is particularly well-suited to flows involving discontinuities, such as shocks and contact discontinuities. The method also performs extremely well for smooth flows, although other schemes which do not perform the extra work necessary for the treatment of discontinuities might be more efficient in these cases. The high resolution and accuracy of PPM are obtained by the explicit nonlinearity of the scheme and through the use of intelligent dissipation algorithms, such as monotonicity enforcement and interpolant flattening. These algorithms are described in detail by Colella and Woodward (1984).

A complete description of PPM is beyond the scope of this guide. However, for comparison with other codes, we note that the implementation of PPM in FLASH uses the Direct Eulerian formulation of PPM and the technique for allowing non-ideal equations of state described by Colella and Glaz (1985). For multidimensional problems, FLASH uses second-order operator splitting (Strang 1968). We note below the extensions to PPM that we have implemented.

The PPM algorithm includes a steepening mechanism to keep contact discontinuities from spreading over too many cells. Its use requires some care, since under certain circumstances, it can produce incorrect results. For example, it is possible for the code to interpret a very steep (but smooth) density gradient as a contact discontinuity. When this happens, the gradient is usually turned into a series of contact discontinuities, producing a stair step appearance in one-dimensional flows or a series of parallel contact discontinuities in multi-dimensional flows. Under-resolving the flow in the vicinity of a steep gradient is a common cause of this problem. The directional splitting used in our implementation of PPM can also aggravate the situation. The contact steepening can be disabled at runtime by setting use_steepening = .false..

The version of PPM in the FLASH code has an option to more closely couple the hydrodynamic solver with a gravitational source term. This can noticeably reduce spurious velocities caused by the operator splitting of the gravitational acceleration from the hydrodynamics. In our `modified states' version of PPM, when calculating the left and right states for input to the Riemann solver, we locally subtract off from the pressure field the pressure that is locally supporting the atmosphere against gravity; this pressure is unavailable for generating waves. This can be enabled by setting ppm_modifystates = .true..

The interpolation/monotonization procedure used in PPM is very nonlinear and can act differently on the different mass fractions carried by the code. This can lead to updated abundances that violate the constraint that the mass fractions sum to unity. Plewa and Müller (1999) (henceforth CMA) describe extensions to PPM that help prevent overshoots in the mass fractions as a result of the PPM advection. We implement two of the modifications they describe, the renormalization of the average mass fraction state as returned from the Riemann solvers (CMA eq. 13), and the (optional) additional flattening of the mass fractions to reduce overshoots (CMA eq. 14-16). The latter procedure is off by default and can be enabled by setting use_cma_flattening = .true..

Finally, there is an odd-even instability that can occur with shocks that are aligned with the grid. This was first pointed out by Quirk (1997), who tested several different Riemann solvers on a problem designed to demonstrate this instability. The solution he proposed is to use a hybrid Riemann solver, using the regular solver in most regions but switching to an HLLE solver inside shocks. In the context of PPM, such a hybrid implementation was first used for simulations of Type II supernovae. We have implemented such a procedure, which can be enabled by setting hybrid_riemann = .true..

15.1.3 The unsplit hydro solver

A directionally unsplit pure hydrodynamic solver (unsplit hydro) is an alternate gas dynamics solver to the split PPM scheme. The method basically adopts a predictor-corrector type formulation (zone-edge data-extrapolated method) that provides second-order solution accuracy for smooth flows and first-order accuracy for shock flows in both space and time. Recently, the order of spatial accuracy in data reconstruction for the normal direction has been extended to implement the 3rd order PPM and 5th order Weighted ENO (WENO) methods. This unsplit hydro solver can be considered as a reduced version of the Unsplit Staggered Mesh (USM) MHD solver (see details in Sec:usm_algorithm) that has been available in previous FLASH3 releases.

The unsplit hydro implementation can solve 1D, 2D and 3D problems with added capabilities of exploring various numerical implementations: different types of Riemann solvers; slope limiters; first, second, third and fifth reconstruction methods; a strong shock/rarefaction detection algorithm as well as two different entropy fix routines for Roe's linearized Riemann solver.

One of the notable features of the unsplit hydro scheme is that it particularly improves the preservation of flow symmetries as compared to the splitting formulation. Also, the scheme used in this unsplit algorithm can take a wide range of CFL stability limits (e.g., CFL $<$ 1) for all three dimensions, which is based on using upwinded transverse flux formulations developed in the multidimensional USM MHD solver (Lee, 2006; Lee and Deane, 2009; Lee, 2013).

Table 15.3: Additional runtime parameters for Interpolation Schemes in the unsplit hydro solver (physics/Hydro/HydroMain/unsplit/Hydro_Unsplit)

Variable	Type	Default	Description
order	integer	2	Order of method in data reconstruction: 1st order Godunov (FOG), 2nd order MUSCL-Hancock (MH), 3rd order PPM, 5th order WENO.
transOrder	integer	1	Interpolation order of accuracy of taking upwind biased transverse flux derivatives in the unsplit data reconstruction: 1st, 2nd, 3rd. The choice of using transOrder=4 adopts a slope limiter between the 1st and 3rd order accurate methods to minimize oscillations in upwinding at discontinuities.
slopeLimiter	string	“vanLeer”	Slope limiter: “MINMOD”, “MC”, “VANLEER”, “HYBRID”, “LIMITED”
LimitedSlopeBeta	real	1.0	Slope parameter specific for the “LIMITED" slope by Toro
charLimiting	logical	.true.	Enable/disable limiting on characteristic variables (.false. will use limiting on primitive variables)
use_steepening	logical	.false.	Enable/disable contact discontinuity steepening for PPM and WENO
use_flattening	logical	.false.	Enable/disable flattening (or reducing) numerical oscillations for MH, PPM, and WENO
use_avisc	logical	.false.	Enable/disable artificial viscosity for FOG, MH, PPM, and WENO
cvisc	real	0.1	Artificial viscosity coefficient
use_upwindTVD	logical	.false.	Enable/disable upwinded TVD slope limiter PPM. NOTE: This requires NGUARD=6
use_hybridOrder	logical	.false.	Enable an adaptively varying reconstruction order scheme reducing its order from a high-order to first-order depending on monotonicity constraints
use_gravHalfUpdate	logical	.false.	On/off gravitational acceleration source terms at the half time Riemann state update
use_3dFullCTU	logical	.true.	Enable a full CTU (e.g., similar to the standard 12-Riemann solve) algorithm that provides full CFL stability in 3D. If .false., then the theoretical CFL bound for 3D becomes less than 0.5 based on the linear Fourier analysis.

Table 15.4: Additional runtime parameters for Riemann Solvers in the unsplit hydro solver (physics/Hydro/HydroMain/unsplit/Hydro_Unsplit)

Variable	Type	Default	Description
RiemannSolver	string	“Roe"	Different choices for Riemann solver. “LLF (local Lax-Friedrichs)”, “HLL", “HLLC", “HYBRID", “ROE", and “Marquina"
shockDetect	logical	.false.	On/off attempting to detect strong shocks/rarefactions (and saving flag in "shok" variable)
shockLowerCFL	logical	.false.	On/off lowering of CFL factor where strong shocks are detected, automatically sets shockDetect if on.
EOSforRiemann	logical	.false.	Enable/disable calling EOS in computing each Godunov flux
entropy	logical	.false.	On/off entropy fix algorithm for Roe solver
entropyFixMethod	string	“HARTENHYMAN”	Entropy fix method for the Roe solver. “HARTEN", “HARTENHYMAN"

The above set of runtime parameters provide various types of different combinations that help in obtaining numerical accuracy, efficiency and stability. However, there are some important tips users should know before using them.

• [Extended stencil]: When NGUARD=6 is used, users should also use nxb, nyb, and nzb larger than 2*NGUARD. For example, specifying -nxb=16 in the setup works well for 1D cases. Once setting up NGUARD=6, users still can use FOG, MH, PPM, or WENO without changing NGUARD back to 4.

• [transOrder]: The first order method transOrder=1 is a default and only supported method that is stable according to the linear Fourier stability analysis. The choices for higher-order interpolations are no longer available in this release.

• [EOSforRiemann]: EOSforRiemann = .true. will call (expensive) EOS routines to compute consistent adiabatic indices (i.e., gamc, game) according to the given left and right states in Riemann solvers. For the ideal gamma law, in which those adiabatic indices are constant, it is not required to call EOS at all and users can set it .false. to reduce computation time. On the other hand, for a degenerate gas, one can enable this switch to compute thermodynamically consistent gamc, game, which in turn are used to compute the sound speed and internal energy in Riemann flux calculations. When disabled, interpolations will be used instead to get approximations of gamc, game. This interpolation method has been tested and proven to gain significant computational efficiency and accuracy, giving reliable numerical solutions even for simulating a degenerate gas.

• [Gravity coupling with Unplit Hydro Solvers]: When gravity is included in a simulation using the unsplit hydro and MHD solvers, users can choose to include gravitational source terms in the Riemann state update at $n+1/2$ time step (i.e., use_gravHalfUpdate=.true.). This will provide an improved second-order accuracy with respect to coupling gravitational accelerations to hydrodynamics. It should be noted that current optimized unsplit hydro/MHD codes (e.g., those selected with +uhd, +usm) do not support the runtime parameters use_gravPotUpdate and use_gravConsv of some previous FLASH versions any more.

• [Reduced CTU vs. Full CTU for 3D in the unsplit hydro (UHD) and staggered mesh (USM) solvers]: use_3dFullCTU is a new switch that enhances a numerical stability for 3D simulations in the unsplit solvers using the corner transport upwind (CTU) algorithm by Colella. The unsplit solvers of FLASH are different from many other shock capturing codes, in that neither UHD nor USM solvers need intermediate Riemann solver solutions for updating transverse fluxes in multidimensional problems. This provides a computational efficiency because there is a reduced number of calls to Riemann solvers per cell per time step. The total number of required Riemann solver solutions are two for 2D and three for 3D (except for extra Riemann calls for constraint-transport (CT) update in USM). This is smaller than the usual stabilty requirement in many other codes which needs four for 2D and twelve for 3D in order to provide a full CFL limit (i.e., CFL $<1$).

  In general for 3D, there is another computationally efficient approach that only uses six Riemann solutions (aka, 6-CTU) instead of solving twelve Riemann problems (aka, 12-CTU). In this efficient 6-CTU, however, the numerical stability limit becomes CFL$<0.5$.

  For solving 3D problems in UHD and USM, enabling the new switch use_3dFullCTU=.true. (i.e., full-CTU) will make the solution evolution scheme similar to 12-CTU while requiring to solve three Riemann problems only (again, except for the CT update in USM). On the other hand, use_3dFullCTU=.false. (i.e., reduced-CTU) will be similar to the 6-CTU integration algorithm with a reduced CFL limit (i.e., CFL $<0.5$).

Unsplit Hydro Solver vs. Unsplit Staggered MHD Mesh Solver: One major difference between the unsplit hydro solver and the USM MHD solver is the presence of magnetic and electric fields. The associated staggered mesh configuration required for the USM MHD solver is not needed in the unsplit hydro solver, and all hydrodynamic variables are stored at cell centers.

Stability Limits for both Unsplit Hydro Solver and Unsplit Staggered Mesh Solver: As mentioned above, the two unsplit solvers can take a wide range of CFL limits in all three dimensions (i.e., CFL $<$ 1). However, in some circumstances where there are strong shocks and rarefactions, shockLowerCFL=.true. could be useful to gain more numerical stability by lowering the CFL accordingly (e.g., default settings provide 0.45 for 2D and 0.25 for 3D for the Donor scheme). This approach will automatically revert such reduced stability conditions to any given original condition set by users when there are no significant shocks and rarefactions detected.

Setting up a simulation with the unsplit hydro solver: The default hydro implementation has changed from split to unsplit in FLASH4.4. One can still specify +unsplitHydro (or +uhd for short) in the setup line in order to explicitly request the unsplit hydro solver for a simulation. One needs to specify +splitHydro in the setup line if a split hydro solver is required instead. For instance, a setup call ./setup Sedov -2d -auto +splitHydro will run a Sedov 2D problem using the split PPM hydro solver. Without specifying +unsplitHydro, the default unsplit hydro solver will be selected.

Diffusion terms: Non-ideal terms, such as viscosity and heat conduction, can be included in the unsplit hydro solver for simulating diffusive processes. Please see related descriptions in Sec:non_ideal_MHD.

Non-Cartesian Grid Support: Grid support for non-Cartesian geometries has been revised in the unsplit hydro and MHD solvers in the current release. The supported geometries are (i) 1D spherical (ii) 2D cylindrical in r-z. Please see related descriptions in Sec:Grid geometry.

15.1.3.1 Implementation of Stationary Rigid Body in a Simulation Domain for Unsplit Hydro Solver

An approach to include a single or multiple stationary rigid body (bodies) in a simulation domain has been newly introduced in the unsplit hydro solver. Using this new feature it is possible to add any numbers of solid bodies that are of any shapes inside a computational domain, where a reflecting boundary condition is to be applied at each solid surface. Due to the nature of regualar box-like grid structure in FLASH, the surface of rigid body looks like stair steps at best rather than smooth or round shapes. High refinement levels are recommended at such stair shaped interfaces around the rigid body.

In order to add a rigid body in a simulation, users first need to add a variable called BDRY_VAR in a simulation Config file. The next step is to initialize BDRY_VAR in Simulation_initBlock.F90 in such a way that a positive one is assigned to cells in a rigid body (i.e., solnData(BDRY_VAR,i,j,k)=1.0 ); otherwise a negative one for all other cells (i.e., solnData(BDRY_VAR,i,j,k)=-1.0).

Users can allow high resolutions around the rigid body by promoting BDRY_VAR to be one of the refinement variables (i.e., refine_var_1=“bdry” in flash.par).

The implementation automatically adapts order (a spatial reconstruction order; see Tab:unsplit hydro parameters) in fluid cells that are near the rigid body, reducing any order ($>1$) to order=1 at those fluid cells adjacent to the body. This prohibits any high order (higher than 1) interpolation algorithms from reaching the rigid body data which should not be used when reconstructing high order Riemann states in the adjacent fluid cells.

For this reason there is one stability issue during simulations when order in the fluid cells becomes 1 and hence the local reconstruction scheme becomes a first order Godunov method. For these cells, the multidimensional local data reconstruction-evolution integration scheme reduces to a donor cell method (otherwise globally the corner-transport-upwind method by Colella) which requires a reduced CFL limit (i.e., CFL $<1/2$ for 2D; CFL $< 1/3$ for 3D). In FLASH4.3, a reduced CFL factor is automatically used in such cases; the theoretical reduced CFL limit of $1/{\tt NDIM}$ is further adjusted by hy_cflFallbackFactor.

Two example simulations can be found in Sec:SimulationFlatPlate and Sec:SimulationSedovChamber.

15.1.4 The Volume-of-Fluid Solver

A volume-of-fluid (VOF) solver is an optional capability to the unsplit hydrodynamic solver for maintaining sharp material interfaces. The method adopts the unsplit VOF advection algorithm (Rider & Kothe 1998) for compressible gasses (Miller & Puckett 1996). We assume only two vof fluid components (or multifluid components) that share a common velocity field. In mixed cells the two components can have different densities, temperatures and internal energies, but are assumed to be in pressure equilibrium. This is in contrast to the MultiSpecies unit where the every species shares a common temperature and each species contributes a partial pressure given by its mass fraction.

In the VOF framework we don't track the material interface explicitly. Instead we evolve the volume fraction of consituent fluid components in each computational cell. Interfaces are modelled as piecewise linear in each cell and are reconstructed from the volume fractions in surrounding cells (Youngs 1984, Rider & Kothe 1998). The evolution of the volume fraction for a compressible gas with components labelled by $\alpha$ is

$${{\partial f^\alpha} \over {\partial t}} + \nabla \cdot (\mathbf{u}f^\alpha) = {{f^\alpha \gamma}\over {\gamma^\alpha}}\nabla \cdot \mathbf{u}.$$ (15.10)

$\gamma$ and $\gamma^\alpha$ are the equivalent single fluid and multifluid component adiabatic indices as described in Sec:EosMF.

Unlike in the rest of the hydrodynamics unit where PDEs are solved algebraicly, Eq. 15.10 is solved geometrically. First the unsplit hydrodynamic solver operates as previously described to update the hydro variables for the equivalent single fluid as parameterized in Sec:EosMF. The mass flux at each face will imply an advected volume through that face in the computational cell, which when cut with the reconstructed piecewise linear material interface partitions the volume flux to the VOF fluid components. The advective update to the volume fraction is then

$$f^{\alpha,\text{adv}} = f^{\alpha,n} - \frac{1}{V_\text{cell}} \sum_{\{i,j,k\}} \left ( {V} ^{\alpha}_{i+1/2} - {V}^{\alpha}_{i-1/2} \right ).$$ (15.11)

$\nabla\cdot \mathbf{u}$ is is inferred from the sum of advected volume fraction's difference with unity. The ratio of component volume fluxes can then be used to partition the flux of density and internal energy.

15.1.5 Multitemperature extension for Hydro

Chp:HEDP described the new capabilities in FLASH for modeling High Energy Density Physics (HEDP) experiments and describes the basic theory. These experiments often require a 3T treatment of the plasma as described in Chp:HEDP. Equation (Eqn:3TFull) shows the full set of 3T equations solved by the current version of FLASH. A series of operator splits are used to isolate the hydrodynamic terms from the various source terms. The Hydro unit is responsible for solving the system of equations which includes the hydrodynamic terms, shown in (Eqn:3THydroOnly). These terms describe advection and work. Note this system contains a redundant equation since the total energy equation, (Eqn:3THydroOnlyEnergy), can be written as a sum which includes (Eqn:3THydroOnlyMom), (Eqn:3THydroOnlyIon), (Eqn:3THydroOnlyEle), and (Eqn:3THydroOnlyRad).

A significant challenge exists in solving (Eqn:3THydroOnly) since (Eqn:3THydroOnlyIon), (Eqn:3THydroOnlyEle), and (Eqn:3THydroOnlyRad) contain source terms that involve velocity divergences; these are the work terms. The quantity $\nabla \cdot \boldsymbol v$ is not defined at a shock, and thus directly evaluating this source term is not possible. Two techniques have been implemented in FLASH for solving (Eqn:3THydroOnly) without evaluating the work terms directly. These will be referred to as the entropy advection approach and the RAGE-like approach. These approaches exploit the fact that the existing hydrodynamic solvers (the split and unsplit solvers) already solve the conservation equations for total mass, momentum, and energy. These equations retain the same form in the 3T case, however they are not complete and must be augmented with other equations to close the system since the total pressure is computed using an equation of state that requires knowledge of the properties of ions and electrons independently. For example, in many equations of state, we can write that $P_\mathrm{ele} = P_\mathrm{ele}(\rho, e_\mathrm{ele})$ and $P_\mathrm{ion} = P_\mathrm{ion}(\rho, e_\mathrm{ion})$. Thus $P = P_\mathrm{ele} + P_\mathrm{ion} = P(\rho,e_\mathrm{ele},e_\mathrm{ion})$. In the 1T case, the system can be closed by assuming $T_\mathrm{ele} = T_\mathrm{ion}$.

15.1.5.1 The Entropy Advection Approach

The total entropy is not continuous at a shock. To conserve mass, momentum, and energy, shocks must irreversibly convert kinetic energy to internal energy. A good approximation that can be made is that the electron entropy is continuous across a shock. The entropy advection approach makes this assumption to solve for the state of the ions. The entropy advection approach has had limited testing. It has not been extended to incorporate radiation. Thus, there is no need to include (Eqn:3THydroOnlyRad).

The entropy advection approach solves the first three equations of (Eqn:3THydroOnly) for conservation of total mass, momentum, and energy. Now the system can be closed by solving either (Eqn:3THydroOnlyIon) or (Eqn:3THydroOnlyEle). However, this cannot be done, since those equations have terms that are divergent at shocks. The solution is to add an additional equation which states that electron entropy is advected with the fluid:

$$\frac{\partial}{\partial t} (\rho s_\mathrm{ele}) + \nabla \cdot (\rho s_\mathrm{ele} \boldsymbol v) = 0$$ (15.12)

The electron internal energy, temperature and other properties are then computed using the EOS in a mode which accepts specific electron entropy $s_\mathrm{ele}$ in addition to specific combined internal energy $Te_\mathrm{tot}$ and $\rho$ as inputs. Thus, the solution procedure for the entropy advection scheme is:

• Solve the system of equations defined by (Eqn:3THydroOnlyMass), (Eqn:3THydroOnlyMom), (Eqn:3THydroOnlyEnergy), and (Eqn:3TEntropyAdvect)
• Compute the total specific internal energy, $e_\mathrm{tot}$, by subtracting the kinetic energy from the total energy: $e_\mathrm{tot} = E_\mathrm{tot} - \boldsymbol v \cdot \boldsymbol v / 2$
• Compute the electron specific internal energy using the 3T equation of state: $e_\mathrm{ele} = \mathrm{EOS}(\rho, s_\mathrm{ele}, e_\mathrm{tot})$
• Compute the ion specific internal energy from the total specific internal energy using the kinetic energy and the electron internal energy: $e_\mathrm{ion} = e_\mathrm{tot} - e_\mathrm{ele}$

15.1.5.2 The RAGE-like Approach

The RAGE-like approach is so named because it is identical to the method implemented in the radiation hydrodynamics code RAGE (Gittings, 2008). Verification tests comparing the two codes have shown nearly identical behavior. The RAGE-like is physically accurate in smooth flow, but does not distribute internal energy correctly among the ions, electrons, and radiation field at shocks. This is in contrast to the entropy advection approach which does distribute energy correctly, but has its own limitations.

In general, let $\Delta e_s$ be the change in the internal energy at a particular location over some short time, $\Delta t$. The subscript $s$ refers to either ions, electrons, radiation, or the total specific internal energy. When considering only the hydrodynamic effects, $\Delta e_s = \Delta e_s^\mathrm{adv} + \Delta e_s^\mathrm{work} + \Delta e_s^\mathrm{shock}$, where:

1. $\Delta e_s^\mathrm{adv}$ refers to the change in internal energy due to the advection of internal energy with the fluid
2. $\Delta e_s^\mathrm{work}$ refers to the change in internal energy due to hydrodynamic work. This term is not well defined near shocks.
3. $\Delta e_s^\mathrm{shock}$ refers to changes in internal energy due to shock heating. Shock heating is the necessarily, irreversible conversion of kinetic energy to internal energy which occurs at shock as a consequence of conserving mass, momentum, and energy.

One physically accurate approximation is that $\Delta e_\mathrm{ion}^\mathrm{shock} = \Delta e_\mathrm{tot}^\mathrm{shock}$. The challenge of 3T hydrodynamics lies in dividing these components so that they can be correctly apportioned among the ions, electrons, and radiation field. The entropy advection approach avoids maintains the physically accurate result by solving an equation for electron entropy.

The RAGE-like approach does not apportion shock heating to only the ions. Rather it apportions the quantity $\Delta e_\mathrm{tot}^\mathrm{work} + \Delta e_\mathrm{tot}^\mathrm{shock}$ among the ions, electrons, and radiation field in proportion to the partial pressures of these components. This is consistent with (Eqn:3THydroOnly) in smooth flow, but it not accurate near shocks where the shock heating should only contribute to the change in the ion internal energy. Note that it is possible to isolate internal energy changes due to advection by solving as set of advection equations for the ions, electrons, and radiation field.

Thus, the solution procedure for the RAGE-like approach is:

1. Solve the system of equations defined by (Eqn:3THydroOnlyMass), (Eqn:3THydroOnlyMom), and (Eqn:3THydroOnlyEnergy) and simultaneously solve:
   
   to update the internal energies by including only advection related changes.
2. Compute the change in total specific internal energy over the time step for each computational cell: $\Delta e_\mathrm{tot} = \Delta E_\mathrm{tot} - \boldsymbol v \cdot \boldsymbol v / 2$
3. Compute $\Delta e_\mathrm{tot}^\mathrm{work} + \Delta e_\mathrm{tot}^\mathrm{shock}$ by subtracting the advected energy changes from the total change in internal energy
4. Divide $\Delta e_\mathrm{tot}^\mathrm{work} + \Delta e_\mathrm{tot}^\mathrm{shock}$ amongst the ions, electrons, and radiation field according to the ratio of pressures

15.1.5.3 Use, Implications, and Limitations of Multitemperature Hydro Approaches

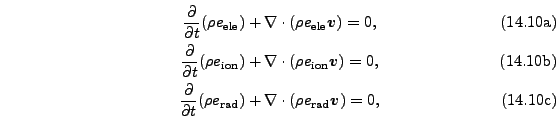Each approach has its own strengths and weaknesses. The entropy advection approach is more accurate in the sense that it correctly includes all shock heating in the ion internal energy. The RAGE-like approach is less accurate near shocks for this reason in terms of predicting the correct downstream ion temperature and electron temperature. In general, immediately downstream of a shock, the RAGE-like approach will predict an electron temperature that is too large and an ion temperature that is too small. However, the density and velocity in the vicinity of shocks will be accurate. Furthermore, ion/electron equilibration (see Chp:HEDP) will quickly act to equalize the ion and electron temperatures. Therefore, the RAGE-like approach is reasonable when the ion/electron equilibration time is small as is the case in many physical scenarios. The Shafranov Shock simulation (see Sec:SimShafShock) compares the temperatures produced by the RAGE-like approach through these two approaches.

The entropy advection approach has some practical limitations that prevent its use in FLASH for general problems. First, many of the 3T EOS models in FLASH do not support the calculation of electron entropy. The only EOS that does is the gamma-law model which is not appropriate modeling many HEDP experiments. Furthermore, oscillations in the electron and ion temperatures have been observed when using this approach. These oscillations can lead to negative ion temperatures. For these reasons, the entropy advection approach has not yet been used for production FLASH simulations of HEDP experiments.

Users can select which 3T hydro approach to use by setting the hy_eosModeAfter runtime parameter. When set to “dens_ie_gather” a RAGE-like approach is used. When set to “dens_ie_sele_gather”, the entropy advection approach is used. Due to the limitations described above, the RAGE-like approach is currently the default option. The +uhd3t setup shortcut can be used to setup a simulation using the 3T extension of the unsplit hydrodynamics solver. The split solver is included by default whenever a multitemperature EOS is included in the simulation. The Shafranov Shock simulation (Sec:SimShafShock) and radiative shock (Sec:SimGrayDiffRadShock) simulations demonstrate the use of the split solver. The Laser Slab simulation (Sec:LaserSlab) demonstrates the use of the 3T unsplit hydrodynamics solver.

The multitemperature hydro extensions are implemented in several implementation directories named multiTemp within the normal hydrodynamic solvers. These contain source files that replace some of the source files of the same name that reside higher in the source tree, and related source and Config files. Together, these files add code functionality and solution variables that are appropriate for multitemperature simulations. The FLASH configuration mechanism automatically takes care of building with the right versions of source files when the multiTemp directories are included.

Table 15.5: Aditional solution variables used with the hydrodynamics (Hydro) unit extended for multitemperature. Note that “specific” variables are understood as per mass unit of the combined fluid.

Variable	Corresponding 1T Variable	Type	Description
tion	temp	GENERIC	ion temperature
tele	temp	GENERIC	electron temperature
trad	temp	GENERIC	radiation temperature
pion	pres	GENERIC	ion pressure
pele	pres	GENERIC	electron pressure
prad	pres	GENERIC	radiation pressure
eion	eint/ener	PER_MASS	specific ion internal energy
eele	eint/ener	PER_MASS	specific electron internal energy
erad	eint/ener	PER_MASS	specific radiation energy
sele		PER_MASS (mass scalar)	specific electron entropy

The Hydro unit thus adds variables that are used to describe the state of each of the three components. In the current version, these are maintained in addition to corresponding variables for the state of the fluid as a whole. There is thus redundancy in the state description. As a benefit of this redundancy, some code units that were written without multitemperature in mind may continue to function in a multitemperature context by referring to the usual 1T set of variables (like temp, pres, ener, eint). The set of variables may be optimized in future code revisions. Table  shows some of the additional variables.

Hydro needs a multitemperature implementation of Eos in oder to work for multitemperature setups. Thus when a simulation is configured to use the multiTemp Hydro code, it also needs to include one of the Eos implementations under physics/Eos/EosMain/multiTemp. The Config files under multiTemp in Hydro will take care of this, but the simulation may have to request a specific implementation under physics/Eos/EosMain/multiTemp. A simuation also needs to control which EOS modes to use during a simulation. Thus the runtime parameters eosMode, eosModeInit, and the new hy_eosModeAfter need to be set appropriately.

15.1.6 Chombo compatible Hydro

This is a slightly modified version of the split Hydro solver (Section Sec:PPM) which must be used when including Chombo  Grid. It is available at physics/Hydro/HydroMain/split/PPM/chomboCompatible and is automatically selected by the setup script whenever an application includes Chombo  Grid.

It is required because the Chombo class LevelFluxRegister which performs flux correction at fine-coarse boundaries has a very different interface to the subroutines in Paramesh. A LevelFluxRegister conserves fluxes at fine-coarse boundaries and then corrects the coarse solution data. In contrast, the Paramesh subroutine Grid_conserveFluxes only conserves fluxes and then FLASH updates the solution data in hy_ppm_updateSoln.

This implementation has not been tested extensively and should not be used in a production simulation. We have encountered worse than expected mass and total energy conservation when it has been used with Chombo  Grid. It is not yet known whether this is a problem with Chombo compatible Hydro or whether our AMR refinement is too aggressive and there is fine-coarse interpolation where there are sharp shock fronts. Aggressive AMR refinement could be the problem because the availability of cell-by-cell refinement in Chombo is very different to our prior experience with Paramesh which refines entire blocks at a time.

An example of bad mass and total energy conservation happens in a Sod problem that uses the included parameter file named test_regular_fluxes_fbs_troublesome.par. The boundary conditions are setup to be periodic, so that mass and total energy should be conserved. Integrated mass and total energy at the end of test problem change by order $1 \times 10^{-5}$%. Increasing lrefine_max from 2 to 4 does not lead to worse conservation. We have found that we can eliminate the conservation problems in this test problem by setting BRMeshRefineBlockFactor = 8 and maxBlockSize = 8, however, such a change has not fixed every test problem configuration which has shown poor conservation. In general, we get better conservation when using mesh parameter values maxBlockSize >= 8, BRMeshRefineBlockFactor >= 8, refRatio = 2 and tagRadius >= 2, and so have added warning messages in the FLASH log file when these values are outside of the given range. We expect to learn more about the conservation issue soon after the FLASH4 release.

This Hydro implementation can be manually included in an application with Paramesh mesh package as follows:

 

./setup Sod -auto chomboCompatibleHydro=True -parfile=test_regular_fluxes_fbs_troublesome.par

The logical parameter chomboLikeUpdateSoln controls whether or not FLASH uses the standard
hy_ppm_updateSoln for the solution update. A value of .true. indicates that it will not be used and is the only acceptable value for Chombo based applications. A value of .false. means it is used and is a possibility for Paramesh based applications.

Using Chombo Compatible Hydro: The runtime parameter eintSwitch should be set to 0.0 when using physics/Hydro/HydroMain/split/PPM/chomboCompatible.