Next: 35.8 3T Shock Simulations Up: 35. The Supplied Test Previous: 35.6 RadTrans Test Problems Contents Index
The neitest problem tests the ability of FLASH to calculate non-equilibrium ionization (NEI) ion abundances. It simulates a stationary plasma flow through a temperature step profile. The solutions were checked using an independent stationary code based on a fifth order Runge-Kutta method with adaptive stepsize control by step-doubling (see Orlando et al. (1999)).
The test assumes a plasma with a mass density of
![]() gm cm
gm cm![]() flowing with a constant uniform velocity of
flowing with a constant uniform velocity of
![]() cm s
cm s![]() through a temperature step between
through a temperature step between ![]() K and
K and
![]() K (cf. Figure 35.74). The plasma is in
ionization equilibrium before going through the jump in the region at
K (cf. Figure 35.74). The plasma is in
ionization equilibrium before going through the jump in the region at
![]() K. The population fractions in equilibrium are obtained
from the equations
K. The population fractions in equilibrium are obtained
from the equations
| (35.55) |
![$\displaystyle \sum_{i=1}^{l_Z} [n_{i}^Z]_{eq} = A_{Z} n_{p}$](img4017.png) |
(35.56) |
The presence of a temperature jump causes a strong pressure
difference, which in turn should cause significant plasma
motions. Since the purpose is to test the NEI module, it is imposed
that the pressure difference does not induce any plasma motion and,
to this end, the hydro variables (namely, ![]() ,
, ![]() , v) are
not updated. In practice, the continuity equations are solved with
uniform density and velocity, while the momentum and energy equations
are ignored.
, v) are
not updated. In practice, the continuity equations are solved with
uniform density and velocity, while the momentum and energy equations
are ignored.
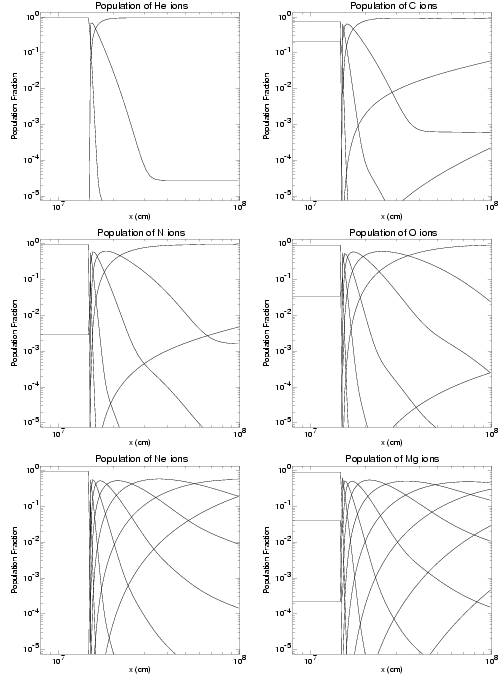
Figure 35.75 shows the population fractions for the 12 most abundant elements in astrophysical plasmas derived with the stationary code (Orlando et al. (1999)). The out of equilibrium ionization conditions are evident for all the elements just after the flow goes through the temperature jump.
 |
The same problem was solved with the NEI module of the FLASH code,
assuming that the plasma is initially in ionization equilibrium at
![]() over all the spatial domain. After a transient lasting
approximately 700 s, in which the population fractions evolve due to
the plasma flow through the temperature jump, the system reaches the
stationary configuration. Outflow boundary conditions (zero-gradient)
are assumed at both the left and right boundaries.
Figure 35.76 shows the population fraction vs. space after
700 s.
over all the spatial domain. After a transient lasting
approximately 700 s, in which the population fractions evolve due to
the plasma flow through the temperature jump, the system reaches the
stationary configuration. Outflow boundary conditions (zero-gradient)
are assumed at both the left and right boundaries.
Figure 35.76 shows the population fraction vs. space after
700 s.
In its default configuration, ConductionDelta models the time development
of a temperature peak that at some time
![]() has the shape of a delta function
in 1D or 3D, subject to heat conduction (with constant coefficient) only.
An ideal gas EOS is assumed.
When using a flux-based Diffuse interface,
the setup includes the Hydro code unit, but changes of the solution due
to hydrodynamical effects are completely suppressed
by zeroing all hydrodynamic fluxes each time
before diffusive fluxes are computed (using
has the shape of a delta function
in 1D or 3D, subject to heat conduction (with constant coefficient) only.
An ideal gas EOS is assumed.
When using a flux-based Diffuse interface,
the setup includes the Hydro code unit, but changes of the solution due
to hydrodynamical effects are completely suppressed
by zeroing all hydrodynamic fluxes each time
before diffusive fluxes are computed (using
![]() );
diffusive fluxes are then computed either by calling
Diffuse_therm (in the +splitHydro case) or
by an calling an internal routine (such as hy_uhd_addThermalFluxes)
of the Hydro unit.
);
diffusive fluxes are then computed either by calling
Diffuse_therm (in the +splitHydro case) or
by an calling an internal routine (such as hy_uhd_addThermalFluxes)
of the Hydro unit.
The theoretical solution of this initial value problem is known:
For any
![]() , the temperature profile is a Gaussian that spreads
self-similarly
over time. In particular in 1D, if the initial condition is defined as
, the temperature profile is a Gaussian that spreads
self-similarly
over time. In particular in 1D, if the initial condition is defined as
| (35.57) |
 |
(35.58) |
  |
See the end of Sec:Diffuse for alternative ways of configuring the test problem, using either a flux-based or a standalone Diffuse interface.
In its default configuration, HydroStatic is set up with constant Gravity. The domain is initialized with density, pressure, etc., fields representing an analytical solution of the hydrostatic problem with the given gravitational acceleration, essentially following the barometric formula.
This initial condition is then evolved in time. Ideally, the solution would remain completely static, and nothing should move. The deviation from this ideal behavior that occurs in practice is a measure of the quality of the discretization of the initial condition, of the hydrodynamics implementation, and of the boundary conditions. The effect of the latter, in particular, can be examined by visualizing artifacts that develop near the boundaries (in particular, velocity artifacts), and studying their dependence on the choice of boundary condition variant.
![\includegraphics[width=0.7\columnwidth]{hybridPIC_yvel}](img4040.png)
|
The LaserSlab simulation provides an example of how to run a realistic, laser driven, simulation of an HEDP experiment. It exercises a wide range of HEDP physics including:
The simulation models a single laser beam illuminating a solid
Aluminum disc in ![]() geometry. The laser is focused on the
geometry. The laser is focused on the ![]() -axis
and enters the domain at a 45 degree angle. The simulation contains
two materials (or “species” in FLASH terminology). These are called
CHAM (short for chamber) and TARG (short for
target). The TARG species models the Aluminum disc. The laser
travels through a low density Helium region before reaching the
Aluminum. The properties of the CHAM species are set to model
the low density Helium. A schematic showing the initial conditions is
shown in Figure 35.80. The laser rays enter just
above the lower-right corner of the domain and travel until they are
absorbed or reflected. The beam intensity is not uniform across the
beam cross section. Rather, it has a super-Gaussian intensity profile
with a 10 micron spot radius.
-axis
and enters the domain at a 45 degree angle. The simulation contains
two materials (or “species” in FLASH terminology). These are called
CHAM (short for chamber) and TARG (short for
target). The TARG species models the Aluminum disc. The laser
travels through a low density Helium region before reaching the
Aluminum. The properties of the CHAM species are set to model
the low density Helium. A schematic showing the initial conditions is
shown in Figure 35.80. The laser rays enter just
above the lower-right corner of the domain and travel until they are
absorbed or reflected. The beam intensity is not uniform across the
beam cross section. Rather, it has a super-Gaussian intensity profile
with a 10 micron spot radius.
The following setup line is used for this simulation:
./setup -auto LaserSlab -2d +cylindrical -nxb=16 -nyb=16 +hdf5typeio \
species=cham,targ +mtmmmt +laser +uhd3t +mgd mgd_meshgroups=6 \
-parfile=example.par
where:
The section “Initial Conditions” section in the runtime parameter
file, “example.par”, sets parameters which define the
initial state of the fluid and also set the properties of the
materials. The first runtime parameters in this section are:
sim_targetRadius = 200.0e-04 sim_targetHeight = 20.0e-04 sim_vacuumHeight = 60.0e-04
| (35.59) | |
| (35.60) |
The next section sets the initial fluid state in the target region and
also sets the properties of the targ species to match
Aluminum. The relevant options are:
# Target material defaults set for Aluminum at room temperature: sim_rhoTarg = 2.7 # Set target material density (solid Al) sim_teleTarg = 290.11375 # Set initial electron temperature sim_tionTarg = 290.11375 # Set initial ion temperature sim_tradTarg = 290.11375 # Set initial radiation temperature ms_targA = 26.9815386 # Set average atomic mass ms_targZ = 13.0 # Set average atomic number ms_targZMin = 0.02 # Set minimum allowed ionization level eos_targEosType = "eos_tab" # Set EOS model to tabulated EOS eos_targSubType = "ionmix4" # Set EOS table file to IONMIX 4 format eos_targTableFile = "al-imx-003.cn4" # Set tabulated EOS file name
A similar set of runtime parameter options exist for the cham
species:
# Chamber material defaults set for Helium at pressure 1.6 mbar: sim_rhoCham = 1.0e-05 sim_teleCham = 290.11375 sim_tionCham = 290.11375 sim_tradCham = 290.11375 ms_chamA = 4.002602 ms_chamZ = 2.0 eos_chamEosType = "eos_tab" eos_chamSubType = "ionmix4" eos_chamTableFile = "he-imx-005.cn4"
For both the targ and cham species, the initial state of the fluid is defined using a density with three temperatures. The initial EOS mode is set using the eosModeInit runtime parameter. It is set to “dens_temp_gather”. This tells FLASH that the initial state will be specified using the density and the temperature.
This simulation uses multigroup radiation diffusion (MGD) to model the
radiation field. This involves setting parameters which control the
MGD package itself and setting parameters which control how opacities
for the two species are computed. The MGD settings from the parameter
file are:
rt_useMGD = .true. rt_mgdNumGroups = 6 rt_mgdBounds_1 = 1.0e-01 rt_mgdBounds_2 = 1.0e+00 rt_mgdBounds_3 = 1.0e+01 rt_mgdBounds_4 = 1.0e+02 rt_mgdBounds_5 = 1.0e+03 rt_mgdBounds_6 = 1.0e+04 rt_mgdBounds_7 = 1.0e+05 rt_mgdFlMode = "fl_harmonic" rt_mgdFlCoef = 1.0 rt_mgdXlBoundaryType = "reflecting" rt_mgdXrBoundaryType = "vacuum" rt_mgdYlBoundaryType = "vacuum" rt_mgdYrBoundaryType = "reflecting" rt_mgdZlBoundaryType = "reflecting" rt_mgdZrBoundaryType = "reflecting"
The next set of parameters tell FLASH how to compute opacities for
each material. In general, the total cell opacity is a number density
weighted average of the opacity of each species in the cell. The
parameters which control the behavior of the opacity unit for this
simulation are:
useOpacity = .true. ### SET CHAMBER (HELIUM) OPACITY OPTIONS ### op_chamAbsorb = "op_tabpa" op_chamEmiss = "op_tabpe" op_chamTrans = "op_tabro" op_chamFileType = "ionmix4" op_chamFileName = "he-imx-005.cn4" ### SET TARGET (ALUMINUM) OPACITY OPTIONS ### op_targAbsorb = "op_tabpa" op_targEmiss = "op_tabpe" op_targTrans = "op_tabro" op_targFileType = "ionmix4" op_targFileName = "al-imx-003.cn4"
This section describes the runtime parameters which control the behavior of the laser in FLASH. Modeling laser energy deposition using ray tracing is fairly complicated and requires large numbers of input parameters. It is highly recommended that you read through the section describing the behavior of the laser model in FLASH to learn more about how the ray tracing algorithms actually work (see Sec:EnergyDeposition).
This simulation uses a single laser beam which travels at an angle of
45 degrees from the ![]() -axis. The “Laser Parameters” section of the
runtime parameters file contains all of the options relevant to
defining the laser beam. The first set of parameters are:
-axis. The “Laser Parameters” section of the
runtime parameters file contains all of the options relevant to
defining the laser beam. The first set of parameters are:
useEnergyDeposition = .true. # Turn on laser energy deposition ed_maxRayCount = 10000 # Set maximum number of rays/cycle/proc to 2000 ed_gradOrder = 2 # Turn on laser ray refraction
The ed_maxRayCount parameter sets the maximum number of rays which can be stored on a given process at once. It tells FLASH how much space to set aside for storing rays. In the case of a single process simulation, ed_maxRayCount must be less than the total number of rays launched on each cycle. The total number of rays launched is set by the ed_numRays_### parameters, described below. Finally, the parameter ed_gradOrder controls how the electron number density and temperature are interpolated within a cell. A value of two specifies linear interpolation.
The next set of parameters are:
ed_laser3Din2D = .true. ed_laser3Din2DwedgeAngle = 0.1
The next set of parameters are:
ed_useLaserIO = .true. ed_laserIOMaxNumPositions = 10000 ed_laserIONumRays = 128
Next, a single laser pulse is defined. Each laser pulse (in this case,
there is only one) represents a specific time history of the power and
multiple pulses can be defined. The LaserSlab simulation has
only a single laser beam which uses laser pulse number 1. The relevant
runtime parameter options are:
# Define Pulse 1: ed_numberOfSections_1 = 4 ed_time_1_1 = 0.0 ed_time_1_2 = 0.1e-09 ed_time_1_3 = 1.0e-09 ed_time_1_4 = 1.1e-09 ed_power_1_1 = 0.0 ed_power_1_2 = 1.0e+09 ed_power_1_3 = 1.0e+09 ed_power_1_4 = 0.0
The next set of parameters define the laser beam itself. The trailing
_1 in the parameter names indicate that these parameters are
associated with the first beam (in this case, the only beam):
ed_lensX_1 = 1000.0e-04 ed_lensY_1 = 0.0e-04 ed_lensZ_1 = -1000.0e-04 ed_lensSemiAxisMajor_1 = 10.0e-04 ed_targetX_1 = 0.0e-04 ed_targetY_1 = 0.0e-04 ed_targetZ_1 = 60.0e-04 ed_targetSemiAxisMajor_1 = 10.0e-04 ed_targetSemiAxisMinor_1 = 10.0e-04 ed_pulseNumber_1 = 1 ed_wavelength_1 = 1.053 ed_crossSectionFunctionType_1 = "gaussian2D" ed_gaussianExponent_1 = 4.0 ed_gaussianRadiusMajor_1 = 7.5e-04 ed_gaussianRadiusMinor_1 = 7.5e-04 ed_numberOfRays_1 = 4096 ed_gridType_1 = "radial2D" ed_gridnRadialTics_1 = 64 ed_semiAxisMajorTorsionAngle_1= 0.0 ed_semiAxisMajorTorsionAxis_1 = "x"
Taken together, the parameters:
![$\displaystyle I(r) = I_0 \exp
\left\{
- \left[ \left( \frac{x}{R_x} \right)^2 + \left( \frac{y}{R_y} \right)^2 \right]^{\gamma}
\right\}$](img4047.png) |
(35.61) |
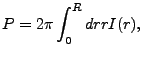 |
(35.62) |
Finally, the user must specify how rays will be spatially distributed
across the beam. The ed_numberOfRays_1 parameter sets the total
number of rays to launch on each time step for each beam. Now we have
to decide how to distribute those rays cross the cross-section of the
laser beam. The parameter ed_gridType_1 is set to
“radial2D”. This means the rays will be laid out on the circular
cross-section of the beam with some radial and angular spacing. The
area of the beam is divided into regions of equal radius and
angle. The parameter ed_gridnRadialTics_1 is set to 64 meaning
that there are 64 radial slices in the beam cross section. Therefore,
there are:
![]() angular slices.
angular slices.
This section describes how the output can be visualized using VisIt
and through other means. LaserIO code in FLASH can be used to
visualize ray paths (see Sec:LaserIO for more
information). The LaserIO unit can only be used with parallel HDF5 IO
implementations. The +hdf5typeio setup option is consistent
with this. The runtime parameters:
ed_useLaserIO = .true. ed_laserIOMaxNumPositions = 10000 ed_laserIONumRays = 128
lasslab_hdf5_plt_cnt_0000 lasslab_hdf5_plt_cnt_0001 ... lasslab_hdf5_plt_cnt_0199 lasslab_hdf5_plt_cnt_0200
After this example LaserSlab simulation is run, the
extract_rays.py script can be used as shown:
»> extract_rays.py lasslab_hdf5_plt_cnt_* Processing file: lasslab_hdf5_plt_cnt_0000 Processing file: lasslab_hdf5_plt_cnt_0001 ... Processing file: lasslab_hdf5_plt_cnt_0198 Processing file: lasslab_hdf5_plt_cnt_0199 Processing file: lasslab_hdf5_plt_cnt_0200 No ray data in "lasslab_hdf5_plt_cnt_0200" skipping...
lasslab_las_0000.vtk lasslab_las_0001.vtk ... lasslab_las_0198.vtk lasslab_las_0199.vtk
The ray data can be plotted on top of the computational mesh. In VisIt, load the lasslab_las_*.vtk database. Add the “RayPower_Watts” Pseudocolor plot. The “RayPower_Watts” plot colors the trajectories based on the power of each ray in units of Watts. Thus, the power of any one ray at any given time should be less than the beam powers specified in the runtime parameters file.
An example showing the ray powers and trajectories is shown in Figure 35.80. The trajectory of 128 laser rays has been drawn. The rays are colored based on their powers.
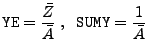 |
Another useful tool in visualizing the behavior of the laser is the FLASH variable DEPO. This variable stores the laser energy deposited in a cell on a particular time step per unit mass. The division by mass removes the geometric factor present in the ray power. The amount of laser energy entering the domain and the amount of laser energy exiting the domain can be used to compute the fraction of laser energy that is deposited. The energy entering and exiting the domain is shown for each cycle and integrated over the entire simulation in the file “lasslab_LaserEnergyProfile.dat”. This file is produced whenever the laser ray tracing package is active in FLASH.
The LaserSlab simulation described previously can be configured to include the ThomsonScattering diagnostic unit. We describe this configuration here to serve as a demonstration for using that unit. See chp:ThomsonScattering for more information on the diagnostic code.
As in the previously described LaserSlab setup,
The simulation models a single laser beam illuminating a solid
Aluminum disc in ![]() geometry. The laser is focused on the
geometry. The laser is focused on the ![]() -axis
and enters the domain at a 45 degree angle. The simulation contains
two materials (or “species” in FLASH terminology). These are called
CHAM (short for chamber) and TARG (short for
target). The TARG species models the Aluminum disc. The laser
travels through a low density Helium region before reaching the
Aluminum. The properties of the CHAM species are set to model
the low density Helium. A schematic showing the initial conditions is
shown in Figure 35.80. The laser rays enter just
above the lower-right corner of the domain and travel until they are
absorbed or reflected. The beam intensity is not uniform across the
beam cross section. Rather, it has a super-Gaussian intensity profile
with a 10 micron spot radius.
-axis
and enters the domain at a 45 degree angle. The simulation contains
two materials (or “species” in FLASH terminology). These are called
CHAM (short for chamber) and TARG (short for
target). The TARG species models the Aluminum disc. The laser
travels through a low density Helium region before reaching the
Aluminum. The properties of the CHAM species are set to model
the low density Helium. A schematic showing the initial conditions is
shown in Figure 35.80. The laser rays enter just
above the lower-right corner of the domain and travel until they are
absorbed or reflected. The beam intensity is not uniform across the
beam cross section. Rather, it has a super-Gaussian intensity profile
with a 10 micron spot radius.
The following setup line is used for this simulation:
./setup -auto LaserSlab -2d -nxb=16 -nyb=16 +hdf5typeio \
species=cham,targ +mtmmmt +laser +uhd3t +mgd mgd_meshgroups=6 \
ed_maxBeams=2 ed_maxPulseSections=4 ed_maxPulses=2 \
thsc_maxBeams=1 thsc_maxPulseSections=4 thsc_maxPulses=1 thsc_maxDetectors=1 \
-parfile=example_thsc.par ThscDemo=True
Here the setup variable ThscDemo is used to turn on the
optional ThomsonScattering configuration of the LaserSlab
setup. This variable is specific to the LaserSlab simulation;
see the end of this simulation's Config file to see how
this is done for LaserSlab and use these ot similar directives
to enable ThomsonScattering for other setups.
Additionally,
The ZPinch simulation provides an example of how to run a realistic, current-driven, simulation of a Z-pinch experiment. It exercises a wide range of HEDP physics including:
The following setup line is used for this simulation:
./setup -auto magnetoHD/ZPinch -1d +cylindrical +ug +usm3t +mtmmmt \
species=fill,line,vacu +mgd mgd_meshgroups=6 +hdf5typeio
The included flash.par file contains many runtime parameters for customization.
Below is a subset of the parameters used in ZPinch:
sim_rhoType = 0 # 0: 0 Gaussians #### DD Fill sim_fill_dens = 30.e-03 sim_fill_minDens = 1.e-05 # used in rhoType 11 sim_fill_ctr = 0. # Gaussian center sim_fill_sigma = 1.0 # rho exp(-r^2/(2*sigma^2)) sim_fill_tele = 1160452.21 # 100 eV (preheated) sim_fill_tion = 1160452.21 # 100 eV sim_fill_trad = 1160452.21 # 100 eV sim_fill_maxTemp = 1.e12 # default, effectively no limit sim_fill_minTemp = 1.e-12 # effectively no limit ms_fillA = 2.014 ms_fillZ = 1.0 eos_fillEosType = "eos_tab" eos_fillSubType = "ionmix4" # set eos table file to ionmix4 format eos_fillTableFile = "DD-006-imx.cn4" # set tabulated eos file name #### Be Liner sim_line_dens = 1.848 sim_line_minDens = 1.e-06 # also acts as density floor for vacuum sim_line_ctr = 1.0 # Gaussian center sim_line_sigma = 0.8 # rho exp(-r^2/(2*sigma^2)) sim_innerRadius = 0.29 # inner radius of the liner sim_thickness = 0.058 # thickness of the liner sim_pert = 0. # pseudo-random density perturbation amplitude sim_seed = 1 # seed for random number generator (makes sims repeatable) sim_line_tele = 5802.26105 # 0.5 eV sim_line_tion = 5802.26105 # 0.5 eV sim_line_trad = 5802.26105 # 0.5 eV sim_line_maxTemp = 1.e12 # default, effectively no limit sim_line_minTemp = 1.e-12 # effectively no limit ms_lineA = 9.012 ms_lineZ = 4. eos_lineEosType = "eos_tab" eos_lineSubType = "ionmix4" # set eos table file to ionmix4 format eos_lineTableFile = "Be-006-imx.cn4" # set tabulated eos file name #### Vacuum (low density Be) sim_vacu_dens = 1.e-05 # rho <= this is vacuum sim_vacu_tele = 5802.26105 # 0.5 eV sim_vacu_tion = 5802.26105 # 0.5 eV sim_vacu_trad = 5802.26105 # 0.5 eV sim_vacu_maxTemp = 5802.26105 # 0.5 eV sim_vacu_minTemp = 5802.26105 # 0.5 eV ms_vacuA = 9.012 ms_vacuZ = 4. eos_vacuEosType = "eos_tab" eos_vacuSubType = "ionmix4" # set eos table file to ionmix4 format eos_vacuTableFile = "Be-006-imx.cn4" # set tabulated eos file name #### Current drive circ_currFile = "current.dat" # filename for current input (ns vs. MA) #circ_voltFile = "Voc_example.dat" # filename for voltage input (circuit model) (s vs. V) #circ_cylLength = 1. # used in 1D sims with circuit model # circuit model restart parameters #circ_initIload = 1.404306536824466661E+07 # these init parameters get used when a restart #circ_initIstack= 1.828569946357272193E+07 # is detected. User should refer to 'circuit.dat' #circ_initVc = 3.834045253898037598E+06 # for the appropriate values to use. #circ_initFlux = 1.724316746860757865E-01 #### trajectory output settings sim_trajOutputInterval = 1.e-10 # output interval for trajectory.dat sim_trajOutputIntervalNearStag = 1.e-11 # output interval near stagnation sim_rNearStag = 0.145 # fuel radius at which <= defines "near stagnation"
Many of the parameters are self-explanatory, or the comments included in the flash.par file suffice. The parameter sim_rhoType controls which density profile is used for initialization; 0 is the default value and is simply constant densities in each region. Other options are 1 (single Gaussian for fill species), 2 (a double Gaussian for fill and line species, summed), and 11 (a double Gaussian for fill and line species, piecewise). The _ctr and _sigma parameters are used for Gaussian profile options. For more details about how sim_rhoType is used, see the Simulation_initBlock.F90 subroutine.
The _minTemp and _maxTemp parameters provide temperature control for each region. These are enforced every timestep in the Simulation_adjustEvolution.F90 subroutine and are typically most useful for the vacuum region. The Simulation_adjustEvolution.F90 subroutine also outputs a file named trajectory.dat, which contains radial positions and moving-average velocities of the inner and outer liner interfaces. The sim_trajOutputInterval, sim_trajOutputIntervalNearStag, and sim_rNearStag parameters provide control of the output frequency of this trajectory data.
The default Config file is set to use the FileInput implementation of the Circuit unit (see Sec:Circuit. Furthermore, the parameter circ_currFile defines the name of the provided current input file as current.dat. Parameters related to the McBride circuit model implementation are commented out; to use this, the user first needs to change the requested implementation in the Config file, resetup, and recompile.
This simulation uses a high constant resistivity for the vacuum and the DaviesWen resistivity coefficients elsewhere. See vacuum resistivity for details on how to control resistivity and Ohmic heating in a vacuum region.
The default parameters included in FLASH give a 1D Z-pinch that stagnates around 160 ns.
The uniform grid settings use 128 cells across the 0.5 cm domain, and iProcs defines the number of processors
to run on (currently set to 32).
In Figure ![[*]](crossref.png) , radial profiles of the azimuthal magnetic field are shown for three
different simulation times. We see that the target pinches due to
, radial profiles of the azimuthal magnetic field are shown for three
different simulation times. We see that the target pinches due to
![]() forces
in a reasonable fashion and the vacuum region maintains a
forces
in a reasonable fashion and the vacuum region maintains a ![]() profile (zero current).
profile (zero current).
There is a 2D version of the flash.par file included, but it likely requires much higher resolution to obtain reasonable results.