Next: 20. Gravity Unit Up: 19. Diffusive Terms Previous: 19. Diffusive Terms Contents Index
The Diffuse unit contains four things:
There are some important differences between other physics units and the flux-based Diffuse implementations:
To use DiffuseFluxBased routines of the Diffuse unit, a simulation should
The appropriate calls to DiffuseFluxBased routines will then be made by the following
Hydro code (which can be found in hy_ppm_sweep.F90):
call Diffuse_therm(sweepDir, igeom, blockList(blk), numCells,&
blkLimits, blkLimitsGC, primaryLeftCoord, &
primaryRghtCoord, tempFlx, tempAreaLeft)
call Diffuse_visc (sweepDir, igeom, blockList(blk), numCells,&
blkLimits, blkLimitsGC, primaryLeftCoord,primaryRghtCoord,&
tempFlx, tempAreaLeft,secondCoord,thirdCoord)
!! call Diffuse_species(sweepDir, igeom, blockList(blk), numCells,&
!! blkLimits, blkLimitsGC, primaryLeftCoord,primaryRghtCoord,&
!! tempFlx, tempFly, tempFlz)
To use the Diffuse unit for heat conduction in a simulation, the runtime parameters useDiffuse and useDiffuseTherm must be set to .true.; and to use the Diffuse unit for viscosity effects in a simulation, the runtime parameters useDiffuse and useDiffuseVisc must be set to .true..
FLASH contains a general purpose implicit diffusion solver that can be used to include physics such as electron thermal conduction and multigroup diffusion. The actual code for these solvers is located in GridSolvers. Two implementations of these solvers exist in the Diffuse unit. An older and less useful version lies under the Split directory. A newer solver which uses the HYPRE library is contained in the Unsplit directory. As the name suggests, the split solver is directionally split (default: Strang) to interact with the pencil grid infrastructure of the GridSolvers/Pfft implementation of the Grid unit. The runtime parameter useDiffuse must be set to .true. to activate the general purpose implicit solver.
The typical diffusion equation that can be solved by this unit takes the form,
In the unsplit solver the equation is implicitly advanced as follows,
In the split solver, the solution is advanced along each direction separately. i.e,
| Scheme | |
| 0.0 | Explicit |
| 0.5 | Crank Nicholson |
| 1.0 | Backward Euler |
Implicitness: It should be noted that the parameters ![]() ,
, ![]() ,
,
![]() are time lagged and evaluated at
are time lagged and evaluated at ![]() . Whereas keeping with the
spirit of the implicit scheme these should have been evaluated at
. Whereas keeping with the
spirit of the implicit scheme these should have been evaluated at
![]() . Evaluating them at
. Evaluating them at ![]() makes the problem non-linear
for non-constant values of
makes the problem non-linear
for non-constant values of ![]() ,
, ![]() and
and ![]() . These equations are much
more complicated to solve. Although time lagged coefficient
essentially linearized the non-linear problem, the trade off is the
scheme is no longer completely implicit. The scheme is fully implicit
only in the constant case. This could
possibly impact the overall stability characteristics of the scheme.
In general, implicit schemes are numerically stable for any time step,
so the runtime parameter dt_diff_factor could be set to a large
value to ignore the diffusion time. However, there are cases in which
HYPRE will have trouble converging on a solution, and decreasing
dt_diff_factor less than 1.0 may resolve the issue.
. These equations are much
more complicated to solve. Although time lagged coefficient
essentially linearized the non-linear problem, the trade off is the
scheme is no longer completely implicit. The scheme is fully implicit
only in the constant case. This could
possibly impact the overall stability characteristics of the scheme.
In general, implicit schemes are numerically stable for any time step,
so the runtime parameter dt_diff_factor could be set to a large
value to ignore the diffusion time. However, there are cases in which
HYPRE will have trouble converging on a solution, and decreasing
dt_diff_factor less than 1.0 may resolve the issue.
The Laplacian term is discretized using a central difference scheme as follows,
Where, ![]() and
and ![]() are cell centered variables, and
are cell centered variables, and
Paramesh: In coming up with a numerical scheme in AMR, it is important to ensure that fluxes are conserved at fine-coarse boundary. This is typically done in FLASH using the Grid_conserveFluxes routine. However this is an option which is not available to the implicit solver. Since it uses HYPRE to solve the linear system, the flux conversation should be embedded in the system being solved by HYPRE.
Looking at standard diffusion equation mentioned earlier, for
simplicity we set ![]() .
.
So,
We introduce a new variable ![]() defined as,
defined as,
We discretize the equation as follows,
The idea is then to compute
![]() on the fine-coarse boundary so as to conserve flux. In a 1D problem
the
on the fine-coarse boundary so as to conserve flux. In a 1D problem
the
![]() on a fine-coarse boundary is computed as
on a fine-coarse boundary is computed as
The idea is similarly extended to 2D where coarse cell flux is set to sum of computed fine cell fluxes
of its neighbors.
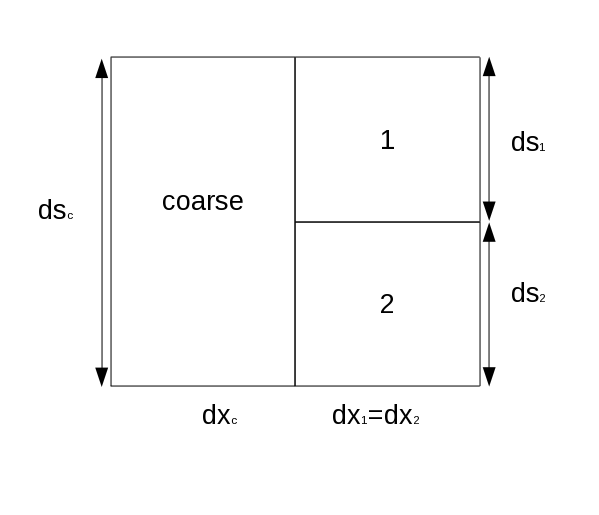
Where,
The value of ![]() can then be evaluated from surrounding cells using paramesh interpolation.
can then be evaluated from surrounding cells using paramesh interpolation.
Usage: To use the “Split” implementation of the Diffuse unit, a simulation should include the Diffuse unit
using an option like -with-unit=physics/Diffuse/DiffuseMain/Split on the setup line, or add
REQUIRES physics/Diffuse/DiffuseMain/Split in the Config file.
To get the “Unsplit” implementation, replace Split with Unsplit.
Split and Unsplit solver are mutually exclusive implementations and cannot exist in the same simulation.
| Capability | Split | Unsplit |
| Paramesh | no | yes |
| Uniform grid | yes | yes |
| Cartesian 1D, 2D | yes | yes |
| Cartesian 3D | yes | yes |
| Cylindrical 1D | yes | yes |
| Cylindrical 2D (R-Z) | yes | yes |
| Spherical 1D | yes | yes |
Unlike much of the rest of FLASH, the general purpose implicit diffusion solver does not implement boundary conditions explicitly through guard cell fills. Instead the diffusion matrix is modified to directly include boundary conditions. The bcTypes and bcValues arguments to Diffuse_solveScalar are used to indicate the boundary condition to use. Each of these arguments is an array of length six corresponding to the six faces of the domain: imin, imax, jmin, imax, kmin, kmax in that order. The bcTypes argument is used to set the type of boundary condition to use. Several integer values are acceptable that are defined in the “constants.h” header file. The allowed integer values and the mathematical effect are shown in Table 19.2. When a Dirichlet (constant value) boundary conditions is required, bcTypes stores the value to use.
The Diffuse unit contains the subroutine
Diffuse_fluxLimiter which modifies a mesh variable representing
a diffusion coefficient over the entire mesh to include a
flux-limit. The subroutine modifies the diffusion coefficient to
smoothly transition to some maximum flux, ![]() . The subroutine
takes the following arguments:
. The subroutine
takes the following arguments:
subroutine Diffuse_fluxLimiter(idcoef, ifunc, ifl, mode, blkcnt, blklst)
The subroutine modifies the mesh variable whose index is given by idcoef by applying a flux-limit. Many methods of incorporating flux-limits into the diffusion coefficient exist. Diffuse_fluxLimiter currently supports three of these: “harmonic”, “min/max”, “Larsen”, and “none”. The mode argument selects the specific method to use. The modes are integers defined in the “constants.h” header file. String representations also exist and can be converted to the integer values using the RuntimeParameters_mapStrToInt subroutine. The string representations can be used to create runtime parameters which represent a flux-limiter mode. Table 19.3 shows the integer constants used as arguments for Diffuse_fluxLimiter as well as the string representations of these constants.
Each flux limiter mode modifies the existing diffusion coefficient to
incorporate the flux limiter in a different way. If ![]() is the
original diffusion coefficient and
is the
original diffusion coefficient and ![]() is the flux-limited
diffusion coefficient then:
is the flux-limited
diffusion coefficient then:
| (19.22) |
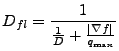 |
(19.23) |
![$\displaystyle D_{fl} = \frac{1}{ \left[ \left(\frac{1}{D}\right)^2 + \left(\frac{\vert\nabla f\vert}{q_{\max}}\right)^2 \right]^{1/2}}$](img2022.png) |
(19.24) |
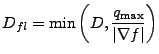 |
(19.25) |
The conductivity is computed by the Conductivity
unit (see Sec:conductivity for more information). This
equation is solved implicitly over a time step to avoid overly
restricted time step constraints. In many cases a flux-limiter is
needed in situations where overly large temperature gradients are
present. The flux-limit used for electron thermal conduction,
![]() , is defined as:
, is defined as:
The Diffuse_solveScalar subroutine is used for the implicit solve. The use of the isotropic thermal diffusion solver is demonstrated in several simulations. See Sec:SimShafShock and Sec:LaserSlab for examples. For thermal diffusion to function, the useConductivity and useDiffuse runtime parameters must be set to .true.. The following runtime parameters control the behavior of the electron and ion thermal conduction package:
The runtime parameters:
diff_eleXlBoundaryType diff_eleXrBoundaryType diff_eleYlBoundaryType diff_eleYrBoundaryType diff_eleZlBoundaryType diff_eleZrBoundaryType diff_ionXlBoundaryType diff_ionXrBoundaryType diff_ionYlBoundaryType diff_ionYrBoundaryType diff_ionZlBoundaryType diff_ionZrBoundaryType
The anisotropic equation (19.31) is solved within the Unsplit scheme of the Diffuse unit. Since it requires magnetic fields, it is also necessary for the code to be using the Unsplit Staggered Mesh (USM) MHD solver (see Sec:usm_algorithm for more details). A setup shortcut has been provided (+supportAnisoCond), which should be used to enable all functionality available for anisotropic thermal diffusion. Additional runtime parameters control the behavior of the anisotropic thermal conduction package:
Slope-limiting for transverse temperature gradients was implemented, because
without it, the
![]() term in (19.31) can
cause heat to flow from a cold cell to a hotter one (a violation of the 2nd law of
thermodynamics). In extreme cases, this can lead to negative temperatures, but
gr_hypreusefloor should be set to .true. with an appropriate value for
gr_hyprefloor (default values are already set to automatocally avoid negative
temperatures during diffusion). If using AMR, the slope-limiter is not applied at
fine/coarse boundaries, so inaccurate temperature decreases are still technically possible.
The default slope-limiter is HYPRESL_MC. HYPRESL_MINMOD is more diffusive,
so it can be used if inaccurate temperature decreases are problematic. To turn off this
slope-limiter feature, use HYPRESL_NONE. In general, a solver such as
HYPRE_GMRES should be used when using a slope-limiter, because slope-limiting
can lead to an asymmetric matrix during the implicit diffusion solve done by HYPRE.
The solver type is set with the runtime parameter gr_hypresolvertype, and the default
value is HYPRE_GMRES when +supportAnisoCond has been used during setup.
If the HYPRE_PCG solver is used, slope-limiting will need to be turned off.
term in (19.31) can
cause heat to flow from a cold cell to a hotter one (a violation of the 2nd law of
thermodynamics). In extreme cases, this can lead to negative temperatures, but
gr_hypreusefloor should be set to .true. with an appropriate value for
gr_hyprefloor (default values are already set to automatocally avoid negative
temperatures during diffusion). If using AMR, the slope-limiter is not applied at
fine/coarse boundaries, so inaccurate temperature decreases are still technically possible.
The default slope-limiter is HYPRESL_MC. HYPRESL_MINMOD is more diffusive,
so it can be used if inaccurate temperature decreases are problematic. To turn off this
slope-limiter feature, use HYPRESL_NONE. In general, a solver such as
HYPRE_GMRES should be used when using a slope-limiter, because slope-limiting
can lead to an asymmetric matrix during the implicit diffusion solve done by HYPRE.
The solver type is set with the runtime parameter gr_hypresolvertype, and the default
value is HYPRE_GMRES when +supportAnisoCond has been used during setup.
If the HYPRE_PCG solver is used, slope-limiting will need to be turned off.
FLASH is able to solve the resistive MHD equations with contributions to the induction equation of the form
| (19.30) | ||
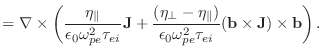 |
(19.31) |
FLASH provides two methods to add resistive MHD to a simulation, either as a contribution to the unsplit Hydro fluxes, or implicitly as a an operator split update using the Unified HYPRE solver. This is controlled with the runtime parameter resistivitySolver. When set to "implicit" the implicit solver is used.
The exact form of the generalized Ohm's Law used in Eq. 19.32 is determined by the parameter resistivityForm and described in Table 19.4. Currently the "implicit" solver only uses the "parallel" form for isotropic resistivity.
| resistivityForm |
|
|
"parallel" |
|
| "perpendicular" |
|
| "fullAniso" |
|
The "implicit" Magnetic Diffusion solver uses the #t#>
| (19.32) | ||
| (19.33) | ||
| (19.34) | ||
| (19.35) | ||
| (19.36) |
In order to supress the generation of spurious
![]() errors Eq. 19.32 may be augmented with a parabolic
divergence cleaning term (Dedner et. al. 2002) that damps the divergence of the magnetic field,
errors Eq. 19.32 may be augmented with a parabolic
divergence cleaning term (Dedner et. al. 2002) that damps the divergence of the magnetic field,
Here the constant ![]() is taken as the maximum value over the whole domain of
is taken as the maximum value over the whole domain of
![]() , where
, where ![]() is the fast magnetosonic speed.
This can be expressed as a
is the fast magnetosonic speed.
This can be expressed as a ![]() tensor
tensor
| (19.38) |
In cylindrical geometries the evolution equations for the radial and axial magnetic field components may still be expressed in conservative
form and so we only need the ![]() tensor in Eqs 19.34 for
tensor in Eqs 19.34 for ![]() . The azimuthal field equation though will introduce
some geometric source terms. These terms can be expressed in the general form of Eq. 8.98, but in particular for problems with
spatially varying resistivity,
. The azimuthal field equation though will introduce
some geometric source terms. These terms can be expressed in the general form of Eq. 8.98, but in particular for problems with
spatially varying resistivity, ![]() , have been observed to introduce numerical artifacts and instability, especially at fine-coarse
boundaries. The conservation form may be restored by evolving
, have been observed to introduce numerical artifacts and instability, especially at fine-coarse
boundaries. The conservation form may be restored by evolving
![]() , which will introduce an additional
, which will introduce an additional ![]() -factor term,
-factor term,
![$\displaystyle \sim \frac{1}{r}\partial_r \left [ r\eta \left ( \partial_r \frac{B_\phi}{r} + \frac{2}{r}\frac{B_\phi}{r} \right ) \right ]$](img2058.png) |
(19.39) | |
| (19.40) |
This form of the equations will be evolved when the grid geometry is "cylindrical" and the runtime parameter diff_conserveAngfield = .TRUE.. This should not be confused with the Hydro runtime parameter conserveAngField, which serves a similar purpose in the MHD solver.
While the above described conservative formulation works well for evoling the magnetic field in cylindrical coordinates, for problems with orders of magnitude difference in resistivity across material interfaces, as is typical in Z-pinch simulations the resultant fields can cause some small scale discrepencies in the calculated ohmic heating at fine-coarse boundaries that can be significantly detrimental to the overall simulation.
To overcome this the finite-volume discretization of Sec. 8.10.4.2 needs to be modified
so that rather than the flux of
![]() being conserved at fine-coarse boundaries the current density
being conserved at fine-coarse boundaries the current density
![]() is conserved.
is conserved.
| (19.41) | ||
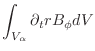 |
![$\displaystyle \approx \frac{V_\alpha r_\alpha}{\Delta r}\left [ \frac{\eta_{\al...
...r_{\alpha-1/2}} \left . \partial_r(rB_\phi) \right \vert _{\alpha-1/2} \right ]$](img2065.png) |
(19.42) |
The boundary conditions imposed on the HYPRE matrix are determined by the the ab_boundary_type runtime parameters Table.
| ab_boundary_type | Description |
| periodic | Periodic (`wrap-around') |
| reflect,reflecting | the normal vector components change sign |
| outflow | Zero-gradient boundary condition in normal direction |
| circuit | Dirichlet boundary condition taken from the Circuit unit |
| user | Dirichlet boundary condition |
The Ohmic heating from magnetic diffusion when using the "implicit" solver is computed from the updated magnetic fields using
the implicit ![]() parameter,
parameter,
In the above ![]() is the rate of heat added to the cell
is the rate of heat added to the cell ![]() at time
at time ![]() . The solver supports two methods for computing
. The solver supports two methods for computing ![]() depending on the runtime parameter
depending on the runtime parameter
![]() . When set to .FALSE.
. When set to .FALSE. ![]() is calculated as a direct centered
difference of
is calculated as a direct centered
difference of
| (19.44) |
In Z-pinch simulations where an artificially high vacuum resistivity is used this discretization this can bias heating into the vacuum at a conductor-vacuum interface since the model doesn't take into account the relative resistence of neighboring cells. When diff_useQohmEdgeMethod = .TRUE. the solver will use a parallel resistor model at cell edges to distribute the current density at an edge to the neighboring cells. A diagram of this model is shown in Fig. 19.2. The equivalent resistence is determined from the resistivity and the geometry of the cell quadrants that meet at the edge. The current density is calculated from finite-differences at the edge center and the total current through the cross-sectional area made up of the joining quadrants. The parallel resistor is solved for the current through each quadrant where the dissipated energy is taken as the ohmic heating in the quadrant. The heating in the entire cell is summed over the contributions from all edges on the cell.
|
[a]  [b]
[b] 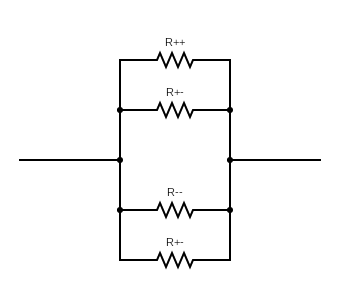
|