23.1 Thermal Conductivity

The Conductivity unit implements a prescription for computing thermal conductivity coefficients used by the Hydro PPM, the unsplit hydro and MHD solvers. The FLASH4 release provides four implementations:

• Constant for heat conduction with a constant isochoric conductivity.
• Constant-diff for heat conduction with a constant coefficient of diffusion.
• SpitzerHighZ which is used for electron thermal conduction. Note that this model can be used with any material.
• LeeMore is another model for electron thermal conduction. Like SpitzerHighZ, it can also be used with any material. The LeeMore model is based on Lee & More (Phys. Fluids, 1984) and should be more accurate than SpitzerHighZ.

To use thermal conductivity in a FLASH4 simulation, the runtime parameter useConductivity must be set to .true. SpitzerHighZ and LeeMore are useful options for realistic HEDP simulations. See Sec:LaserSlab for an example of how the SpitzerHighZ implementation is used in a realistic simulation.

The Spitzer conductivity implemented here is shown in (Eqn:CondSpitzerHighZ). It is consistent with the value given in (Atzeni, 2004).

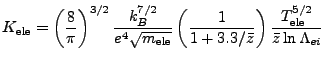$$K_\mathrm{ele} = \left( \frac{8}{\pi} \right)^{3/2} \frac{k_B^{7/... ...}{1 + 3.3/\bar z} \right) \frac{T_\mathrm{ele}^{5/2}}{\bar{z} \ln \Lambda_{ei}}$$ (23.1)

where:

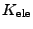• $K_\mathrm{ele}$ is the electron conductivity
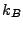• $k_B$ is the Boltzmann constant
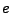• $e$ is the electron charge
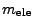• $m_\mathrm{ele}$ is the mass of an electron
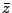• $\bar z$ is the average ionization as computed by the EOS
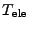• $T_\mathrm{ele}$ is the electron temperature
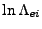• $\ln \Lambda_{ei}$ is the Coulomb logarithm associated with electron-ion collisions and is discussed in Sec:Heatexchange.

At high temperatures, LeeMore and SpitzerHighZ are nearly identical aside from differences in the treatments of the Coulomb logarithm (Sec:HeatexchangeLeeMore). At lower temperatures there can be substantial differences between LeeMore and SpitzerHighZ and generally the LeeMore model should be much more accurate. This is because SpitzerHighZ incorrectly assumes that the material remains a classical plasma even at low temperatures. In practice, however, it is often the case in HEDP simulations that the laser heating will rapidly bring the material to the temperatures where the classical plasma approximation is valid and the differences between SpitzerHighZ and LeeMore will be minimal.

Users are encouraged to experiment with using both the SpitzerHighZ and LeeMore models in HEDP simulations in order to determine the sensitivity of the results to the electron thermal conductivity model. Although LeeMore should always be much more accurate than SpitzerHighZ, there may be cases where the LeeMore model may still not be accurate enough for a specific application. It is well known that some materials do not agree well with the LeeMore prediction in certain density-temperature regimes (e.g. Desjarlais et al. 2002).

23.1.1 Anisotropic Thermal Conductivity

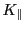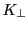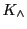There are now implementations within the Conductivity unit which calculate and use anisotropic thermal conductivities. For full functionality, users should include the setup shortcut +supportAnisoCond in their setup command. This will enable the code to calculate and store the thermal conductivities $K_{\parallel}$, $K_{\perp}$, and $K_{\wedge}$ (Righi-Leduc). If the user chooses to use one of the anisotropic thermal conductivity implementations without this setup shortcut, and without turning on relevant logical switches in their flash.par file, the code will do isotropic thermal diffusion with the 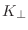$K_\perp$ coefficient. This is most suitable for 1D and 2D problems in which the B-field is only into or out of the page. Otherwise, it only makes sense to use these conductivites in conjuction with the anisotropic thermal diffusion solver (see Sec:AnisoDiffusion for more information).

There are two implementations that calculate aniostropic coefficients:

• EppHain gives coefficients defined by Epperlein & Haines (Phys. Fluids, 1986).
• JiHeld gives coefficients defined by Ji & Held (Phys. Plasmas, 2013).

These are currently two of the most accurate implementations in the code (for MHD simulations), and should be strongly considered for use in magnetic HEDP applications. Alternatively, the user may choose to use constant coefficents by using the ConductivityMain/Constant implementation. In this case, the following runtime parameters should be defined:

• cond_constantParallel: thermal conductivity $K_{\parallel}$
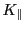
• cond_constantPerpendicular: thermal conductivity $K_{\perp}$
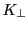
• cond_constantCross: thermal conductivity $K_{\wedge}$

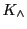
Note that the current implementation does not allow for different constant values for electrons and ions, thus the Constant implementation should not be used for physically realistic 3T applications.

For a more detailed description of how to control anisotropic thermal diffusion, see Sec:AnisoDiffusion.