Subsections

18.5 Heatexchange

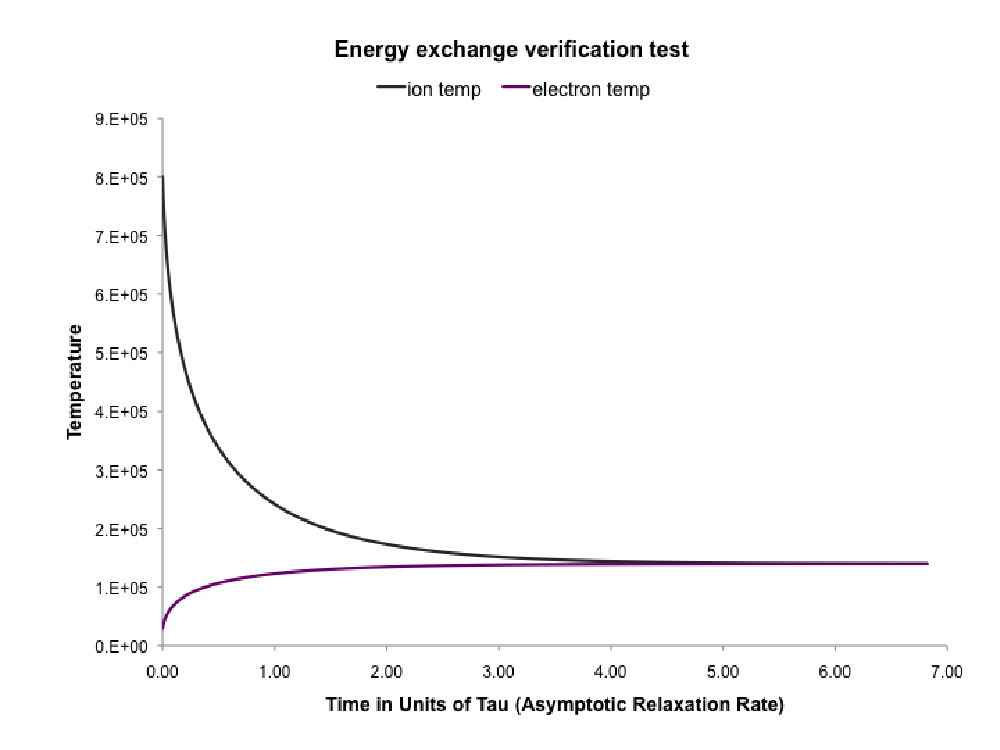
The Heatexchange unit implements coupling among the different components (Ion, Electron, Radiation) as a simple relaxation law.

$\displaystyle \frac{\partial \rho E_{Ele}}{\partial t} = \kappa_{i,e}(T_{Ion}-T_{Ele}) + \kappa_{e,r}(T_{Rad}-T_{Ele})$			(18.263)
$\displaystyle \frac{\partial E_{Rad}}{\partial t} = -\kappa_{e,r}(T_{Rad}-T_{Ele})$			(18.264)
$\displaystyle \frac{\partial \rho E_{Ion}}{\partial t} = -\kappa_{i,e}(T_{Ion}-T_{Ele})$			(18.265)

This unit is required because FLASH operator splits the electron-ion equilibration term from the rest of the calculations. All realistic 3T HEDP simulations should include the Heatexchange unit since it is responsible for equilibrating the ion/electron temperatures over time. The radiation terms in (Eqn:energyexchange) are only included when the legacy gray radiation diffusion unit is used. The more sophisticated multigroup radiation diffusion unit, described in chp:RadTrans, includes the emission and absorption internally.

There are several different implementations residing under Heatexchange unit,

Immediate: Instantaneous complete equilibration.
Constant: hx_couplingConst12, hx_couplingConst13 and hx_couplingConst23 can be used for setting the constant coupling terms.
ConstCoulomb: Uses a constant coulomb logarithm to compute electron-ion equilibration.
hx_coulombLog can be used to set this value.
Spitzer: Uses a Spitzer electron-ion equilibration timescale.
LeeMore: Uses a Spitzer-like electron-ion equilibration timescale but with the Coulomb logarithm from Lee & More 1984.

The Constant and ConstCoulomb implementations are really designed to be used for testing purposes. The Spitzer and LeeMore implementation should be used for simulations of actual HEDP experiments since it is more accurate and physically realistic. This is described in detail in Sec:HeatexchangeSpitzer and Sec:HeatexchangeLeeMore.

hx_relTol runtime parameter affects the time step computed by Heatexchange_computeDt. Basically, if the max (abs) temperature adjustment that would be introduced in any nonzero component in any cell is less than hx_relTol, then the time step limit is relaxed. Set to a negative value to inherite the value of runtime parameter eos_tolerance.

Usage: To use any implementation of Heatexchange unit, a simulation should include the Heatexchange using an option like -with-unit=physics/sourceTerms/Heatexchange/HeatexchangeMain/ConstCoulomb on the setup line, or add
REQUIRES physics/sourceTerms/Heatexchange/HeatexchangeMain/ConstCoulomb in the Config file. The same process can be repeated for other implementations.Constant implementation is
set as the default.

**Figure 18.20:** Verification test for heat exchange code units, showing electrons and ions at different temperatures coming into mutual equilibrium, as expected from the form of the electron-ion coupling. The time axis unit is equal to the asymptotic value of the exponential decay time.

18.5.1 Spitzer Heat Exchange

The Spitzer implementation described here and LeeMore implementation described later in Sec:HeatexchangeLeeMore should be used to model electron-ion equilibration in realistic HEDP simulations. See Sec:LaserSlab for an example of how to use the Spizter Heatexchange implementation in an HEDP simulation. Note, that this implementation only models electron-ion equilibration, and does not include any radiation related physics. In that sense it is designed to be used in conjunction with the multigroup radiation unit described in diffusion chp:RadTrans, since this unit includes the emission and absorption terms internally. Thus the equations solved by the Spitzer implementation are:

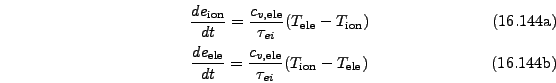$\begin{subequations}\begin{gather}\frac{d e_{\mathrm{ion}}}{dt} = \frac{c_{v,\ma... ...}}}{\tau_{ei}} ( T_\mathrm{ion} - T_\mathrm{ele}) \end{gather}\end{subequations}$

where:

$T_\mathrm{ele}$ is the electron temperature
$T_\mathrm{ion}$ is the ion temperature
$e_\mathrm{ele}$ is the electron specific internal energy
$e_\mathrm{ion}$ is the ion specific internal energy
$c_{v,\mathrm{ele}}$ is the electron specific internal energy
$\tau_{ei}$ is the dlectron-ion equilibration time

We then replace with for the ions and electrons to obtain:

$\begin{subequations}\begin{gather}\frac{d T_{\mathrm{ion}}}{dt} = \frac{m}{\tau_... ...{1}{\tau_{ei}} ( T_\mathrm{ion} - T_\mathrm{ele}) \end{gather}\end{subequations}$

where $m = c_{v,\mathrm{ele}} / c_{v,\mathrm{ion}}$ is the ratio of specific heats. (Eqn:HxSpitzerEqns) can be solved by assuming that the specific heats and electron-ion equilibration times are constant over a time step, $\Delta t$ . The result is that the ion/electron temperatures equilibrate exponentially over a time step. This is shown in (Eqn:HxSpitzerSolns).

$\begin{subequations}\begin{gather}T_\mathrm{ion}^{n+1} = \left( \frac{T_\mathrm{... ... \left[ -(1+m) \frac{\Delta t}{\tau_{ei}} \right] \end{gather}\end{subequations}$

The Spitzer implementation does not directly update the temperatures, however, since this would lead to energy conservation errors. Rather, the specific internal energies are directly updated according to:

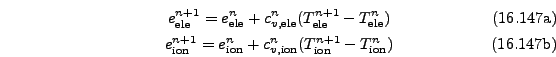$\begin{subequations}\begin{gather}e_\mathrm{ele}^{n+1} = e_\mathrm{ele}^n + c_{v... ...ion}}^n (T_\mathrm{ion}^{n+1} - T_\mathrm{ion}^n) \end{gather}\end{subequations}$

The final temperatures are then computed using a call to the equation of state.

The subroutine PlasmaState_ieEquilTime is responsible for computing the electron-ion equilibration time, $\tau_{ei}$ . Currently, the formula used is consistent with that given in (Atzeni, 2004) and the NRL Plasma Formulary (Huba, 2011). The value of $\tau_{ei}$ is shown in (Eqn:HxSpitzerIeTime).

$\displaystyle \tau_{ei} = \frac{3 k_B^{3/2}}{8 \sqrt{2 \pi} e^4} \frac{ \left(m... ...{ele} m_\mathrm{ion}\right)^{1/2} {\bar z}^2 n_\mathrm{ion} \ln \Lambda_{ei} }.$

(18.270)

where:

is the Boltzmann constant
is the electron charge
$m_\mathrm{ion}$ is the average mass of an ion
$m_\mathrm{ele}$ is the mass of an electron
$\bar z$ is the average ionization as computed by the EOS
$n_\mathrm{ion}$ is the ion number density in the plasma
$\ln \Lambda_{ei}$ is the Coulomb Logarithm associated with electron-ion collision, further description below.

The Coulomb logarithm is the logarithmic ratio of the maximum impact parameter, $b_{\mathrm{max}}$ , to minimum impact parameter, $b_{\mathrm{min}}$ , for electron-ion collisions, i.e.,

$\displaystyle \ln \Lambda_{ei} = \ln \left[1 + (\frac{b_{\mathrm{max}}}{b_{\mathrm{min}}} \right]$

(18.271)

In general, the scales of $b_{\mathrm{min}}$ and $b_{\mathrm{max}}$ should be well separated and therefore the Coulomb logarithm should always be a dimensionless, positive number with a value of a few or greater. The expressions for $b_{\mathrm{max}}$ and $b_{\mathrm{min}}$ used in the Spitzer heat exchange are given by (Brysk, 1974),

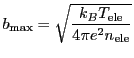$\displaystyle b_{\mathrm{max}} = \sqrt{\frac{k_B T_\mathrm{ele}}{4\pi e^2 n_\mathrm{ele} } }$

(18.272)

and

$\displaystyle b_{\mathrm{min}} = \max \left( \frac{\bar z e^2 }{ 3 k_B T_\mathr... ...}} \;,\; \frac{\hbar} { 2 \sqrt{3 k_B T_\mathrm{ele} m_\mathrm{ele}}} \right) .$

(18.273)

where $n_\mathrm{ele}$ is the electron number density and $\hbar$ is Planck's constant.

Note that in HED plasmas, there are situations where $b_{\mathrm{max}} \sim b_{\mathrm{min}}$ resulting in a very small or negative value. Therefore, the Coulomb logarithm is forced to be greater than or equal to 1.0 by default (as in Brysk, 1974). This floor value can be changed by setting the runtime parameter logLambdaFloor.

Finally, note that the runtime parameter hx_ieTimeCoef multiplies $\tau_{ei}$ and can be used to scale $\tau_{ei}$ .

18.5.2 LeeMore Heat Exchange

The LeeMore heat exchange uses (Eqn:HxSpitzerIeTime), but with a different expression for the Coulomb logarithm, $\ln \Lambda_{ei}$ . The expression for $\ln \Lambda_{ei}$ comes from Sec. III.B. of Lee & More 1984,

$\displaystyle \ln \Lambda_{ei} = \frac{1}{2} \ln \left[ 1 + \left( \frac{b_{\mathrm{max}}}{b_{\mathrm{min}}} \right)^2 \right]$

(18.274)

where $b_{\mathrm{max}}$ is equal to the Debye-Huckel screening length, $\lambda_{\rm DH}$ , in an expression that includes the ion temperature and mean ionization state,

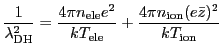$\displaystyle \frac{1}{\lambda_{\mathrm{DH}}^2} = \frac{4 \pi n_{\mathrm{ele}} ... ...mathrm{ele}}} + \frac{4 \pi n_{\mathrm{ion}} (e \bar{z})^2}{k T_{\mathrm{ion}}}$

(18.275)

and $b_{\mathrm{min}}$ is the same as used in the Spitzer heat exchange model, i.e. (Eqn:Hxbmin).

Like the Spitzer heat exchange model, the Coulomb logarithm in the LeeMore heat exchange is forced to be greater or equal to logLambdaFloor. Lee & More 1984 cite numerical results that conclude that the floor on the Columb logarithm should be 2.0 (instead of 1.0 as in the Spitzer heat exchange model).

It should be reiterated that the LeeMore heat exchange model just described only differs from the Spitzer heat exchange in the calculation of the Coulomb logarithm. The expression in Lee & More 1984 for the electron relaxation time (their Eq. 24) also contains Fermi-Dirac factors that we neglect here for simplicity. These factors may be incorporated into the LeeMore heat exchange model at a later date. Regardless, the LeeMore heat exchange module should be more accurate than the Spitzer heat exchange because of the improvement to the Coulomb logarithm.