Subsections
18.4 Energy Deposition Unit
The Energy Deposition unit calculates the energy deposited by one or more laser beams incident upon
the simulation domain. The function EnergyDeposition is the main
control driver of the Energy Deposition unit.
The current implementation treats the laser beams in the geometric optics
approximation. Beams are made of a number of rays whose paths are traced through the domain based
on the local refractive index of each cell. The laser power deposited in a cell is calculated based
on the inverse Bremsstrahlung power in the cell and depends on the local electron number density
gradient and local electron temperature gradient. Currently there are two schemes implemented into
FLASH: 1) a ray tracing algorithm based on cell average quantities and 2) a more refined
ray tracing method based on cubic interpolation. Both schemes are discussed in the algorithmic
implementation section 18.4.4 below.
18.4.1 Ray Tracing in the Geometric Optics Limit
In the geometric optics approach, the path of a laser wave can be described as the motion of a
ray of unit-mass through the potential field
where 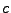 is the speed of light in vacuum and
is the speed of light in vacuum and 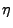 is the index of refraction of the medium, assumed
to vary on a much longer spatial scale than the wavelength of the laser wave. Also
is the index of refraction of the medium, assumed
to vary on a much longer spatial scale than the wavelength of the laser wave. Also
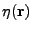 is considered constant during the time it takes for the ray to cross the domain (frozen medium).
However
is considered constant during the time it takes for the ray to cross the domain (frozen medium).
However
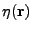 is allowed to vary from one time step to the next. For a non-relativistic
unmagnetized plasma, the refractive index is given by
is allowed to vary from one time step to the next. For a non-relativistic
unmagnetized plasma, the refractive index is given by
where
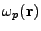 is the plasma frequency,
is the plasma frequency, 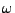 the laser frequency,
the laser frequency,
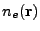 is
the electron number density at location
is
the electron number density at location 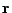 and
and
is the critical density at which the ray frequency and the plasma frequency are equal (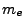 and
and 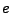 are the electron mass and charge,
are the electron mass and charge, 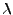 is the laser wavelength). The ray equation of motion is then
is the laser wavelength). The ray equation of motion is then
which constitutes the basic ray tracing 2nd order ODE equation. Splitting into two 1st order ODEs leads to
For short distances we can assume a first order Taylor expansion of the electron number density around a
specific location 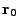 :
:
where
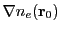 is the electron number density gradient vector at
is the electron number density gradient vector at 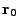 . A consequence
of this short distance approximation is that the electron number density gradient vectors at
. A consequence
of this short distance approximation is that the electron number density gradient vectors at 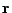 and
and 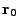 are equal. For separable 1st order ODEs (cartesian) we can write the following equations
for the ray velocity and position as a function of time
are equal. For separable 1st order ODEs (cartesian) we can write the following equations
for the ray velocity and position as a function of time
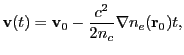 |
|
|
(18.40) |
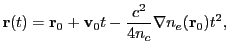 |
|
|
(18.41) |
where 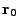 and
and 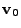 are the initial ray position and velocity. For non-separable 1st order ODEs,
like for example cylindrical or spherical coordinates (see below), we cannot state analytical equations
for the ray velocity and position as a function of time, and we must solve the set of 1st order ODEs using
specific numerical methods like for example Runge-Kutta (RK).
are the initial ray position and velocity. For non-separable 1st order ODEs,
like for example cylindrical or spherical coordinates (see below), we cannot state analytical equations
for the ray velocity and position as a function of time, and we must solve the set of 1st order ODEs using
specific numerical methods like for example Runge-Kutta (RK).
18.4.2 Laser Power Deposition
The power 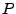 of an electromagnetic wave is depleted by the inverse Bremsstrahlung (ib) process.
The rate of power loss is governed by a 1st order ordinary differential equation (ODE):
of an electromagnetic wave is depleted by the inverse Bremsstrahlung (ib) process.
The rate of power loss is governed by a 1st order ordinary differential equation (ODE):
The inverse Bremsstrahlung frequency factor is given by the formula
where 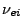 is the electron-ion collision frequency
is the electron-ion collision frequency
Here 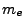 is the electron mass,
is the electron mass, 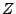 is the average ionization number of the plasma,
is the average ionization number of the plasma, 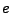 is the electron charge,
is the electron charge,
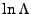 is the Coulomb logarithm,
is the Coulomb logarithm, 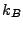 is the Boltzmann constant and
is the Boltzmann constant and 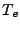 is the electron temperature.
The Coulomb logarithm is the natural logarithm of the Debye number
is the electron temperature.
The Coulomb logarithm is the natural logarithm of the Debye number 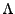 and is taken here as
and is taken here as
The inverse Bremsstrahlung frequency depends thus on the electron number density and the electron temperature,
both of which are functions of the position, and, since the position changes with time, it ultimately
is also a function of time
Solution of the above ODE in Eq.(18.42) gives the attenuation of the ray's power
from time zero to time 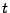 :
:
For a given small time step, the integral in Eq.(18.47) can be approximated in the following
way. In order to remove the intermediate function
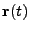 from the expression in Eq.(18.46),
we first assume that the Coulomb logarithm remains constant during the incremental time step
from the expression in Eq.(18.46),
we first assume that the Coulomb logarithm remains constant during the incremental time step
Using first order Taylor expansions on both 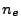 and
and 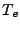 similar to equation 18.39
similar to equation 18.39
and inserting the ray position equation 18.41, we get
The inverse-Bremsstrahlung rate can thus be written as a rational polynomial expression
where
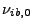 is the inverse-Bremsstrahlung rate at the initial point (zero time)
is the inverse-Bremsstrahlung rate at the initial point (zero time)
and
 |
 |
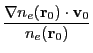 |
(18.55) |
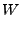 |
 |
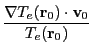 |
(18.56) |
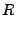 |
 |
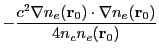 |
(18.57) |
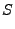 |
 |
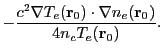 |
(18.58) |
The integral in Eq.(18.47) can be solved by using a second order Gaussian quadrature
where
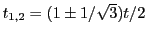 and both weights are equal to 1. The rate of energy deposition
(energy deposited per unit time) during this time is then
and both weights are equal to 1. The rate of energy deposition
(energy deposited per unit time) during this time is then  .
.
18.4.3 Laser Energy Density
Implemented only for 3D Cartesian geometry and 2D cylindrical geometry with ed_laser3Din2D ray tracing in FLASH 4.5.
Light carries energy through space and therefore can be attributed an energy density (energy per volume). For example, light propagating at velocity 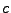 with power
with power 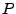 through an area
through an area 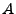 has an energy density of
has an energy density of
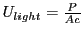 .
.
Splitting the laser's power across a finite number of rays is an abstraction with an interesting consequence. Because each ray's power is artificially confined to a 1D curvilinear axis, light rays in FLASH are naturally described by linear energy densities (energy per distance) rather than volumetric energy densities (energy per volume). Volumetric energy density is more physically relevant. Therefore, the contribution of each ray to volumetric laser energy density (a cell quantity, “lase”, available as an output when using certain ray-tracing modules - see 18.4.11.5) is calculated by taking the linear energy density of each ray, integrating over the ray path within the cell, and dividing by the cell volume.
The details of the laser energy density calculation are as follows. Trading path length for parametrized time, ray power 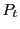 changes along the ray path by Eq.(18.47). For light traveling at speed
changes along the ray path by Eq.(18.47). For light traveling at speed 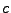 (determined by frequency and medium), ray linear energy density
(determined by frequency and medium), ray linear energy density 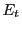 similarly varies along ray path:
similarly varies along ray path:
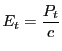 |
|
|
(18.60) |
Volumetric energy density 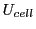 is found by integrating linear energy density
is found by integrating linear energy density 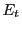 over the ray's path within the cell (
over the ray's path within the cell (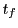 is the parametrized time value for which the ray reaches edge of cell), then dividing by cell volume
is the parametrized time value for which the ray reaches edge of cell), then dividing by cell volume 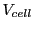 :
:
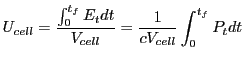 |
|
|
(18.61) |
For each cell, all contributions to volumetric laser energy density (all rays'  ) are summed to give a total laser energy density for that cell.
) are summed to give a total laser energy density for that cell.
18.4.4 Algorithmic Implementations of the Ray Tracing
The current implementation of the laser energy deposition assumes that rays transit the entire domain
in a single time step. This is equivalent of saying that the domain's reaction time
(changes of its state variables) is much longer than the time it takes for each ray to either
cross the domain or get absorbed by it. For each time step it is first checked, if at least one of the
laser beams is still active. If this is the case, then for each active beam a collection of rays
is generated possessing the right specifications according to the beam's direction of firing, its
frequency, its pulse shape and its power. The Energy Deposition unit moves all rays across
all blocks until every ray has either exited the domain or has been absorbed by the domain.
The rays are moved on a block by block basis and for each block the rays are traced through the
interior cells. The Energy Deposition unit utilizes the infrastructure from the Grid Particles
unit 8.9 to move rays between blocks and processors. The code structure of the Energy
Deposition unit during one time step is as follows:
Loop over all blocks containing rays
Calculate needed block data for all cells.
- ------- Start threading --------
- Loop over all rays in block
Trace each ray through all cells in block
- End loop
- ------- End threading --------
End loop
Reassign rays to blocks/processors and repeat (exit, if no more rays)
The inner loop over all rays in a block is conveniently handled in one subroutine to
allow for compact (optional) threading. Currently there are three algorithmic options on how to
trace the rays in FLASH: 1) Cell average algorithm, 2) Cubic interpolation with piecewise
parabolic ray tracing and 3) Cubic interpolation using Runge Kutta integration schemes.
18.4.4.1 Cell Average (AVG) Algorithm
The AVG algorithm (Kaiser 2000) is based on tracing the rays on a cell-by-cell basis. Each cell has its own
average center electron number density
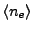 and electron temperature
and electron temperature
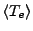 value at the center of the cell. The electron number density gradient vector
value at the center of the cell. The electron number density gradient vector
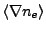 as
well as the electron temperature gradient vector
as
well as the electron temperature gradient vector
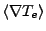 are assumed to be constant within each cell. Rays will be transported through each cell between cell faces
in one step. Electron number densities
are assumed to be constant within each cell. Rays will be transported through each cell between cell faces
in one step. Electron number densities 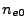 and electron temperatures
and electron temperatures 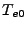 on the entry cell face are
calculated from the cell center values in accordance with equation 18.39 using first order
Taylor expansions
on the entry cell face are
calculated from the cell center values in accordance with equation 18.39 using first order
Taylor expansions
where 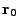 are the position coordinates of the ray at the cell's face and
are the position coordinates of the ray at the cell's face and
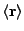 are the coordinates of the cell's center. The ray's cell crossing time
are the coordinates of the cell's center. The ray's cell crossing time
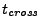 is determined from the quadratic time equation 18.41 by inserting
planar equations
is determined from the quadratic time equation 18.41 by inserting
planar equations
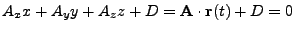 for all cell faces (in cartesian coordinates),
leading to
for all cell faces (in cartesian coordinates),
leading to
and selecting the shortest time (excluding the zero time corresponding to the point of entry). In FLASH, the
cartesian cell faces are coplanar with the xy-, xz- and the yz-plane, simplifying the quadratic time equation.
A cell face located at 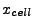 and coplanar with the yz-plane has the plane equation
and coplanar with the yz-plane has the plane equation
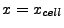 and thus
and thus
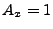 ,
, 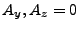 and
and
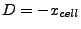 . For this cell face, the quadratic time equation becomes
. For this cell face, the quadratic time equation becomes
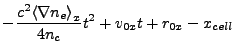 |
 |
0 |
(18.65) |
and similar for the other cartesian components. In order to achieve a stable ray tracing algorithm and
uniquely assign rays to cells and blocks while crossing through cell walls, a cell wall thickness is
defined, which is shared between two adjacent cells. The code is set up such that rays are never to
be found inside this wall. When crossing between two cells occurs (same block or different blocks), the
rays positions are always adjusted (nudged) such that they will sit on this wall with finite thickness.
The cell wall thickness is defined in the code as being a very tiny fraction (adjustable, with default value
of 1:1,000,000) of the smallest cell dimension during a simulation.
The ray's rate of energy deposition between the cell entry face and the cell exit face is calculated using
equations 18.47 to 18.59 with
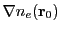 and
and
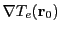 replaced by their cell average values
replaced by their cell average values
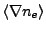 and
and
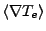 and
and
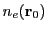 and
and
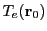 replaced by their corresponding cell entry values
replaced by their corresponding cell entry values 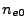 and
and 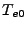 .
The upper integration time limit is
.
The upper integration time limit is 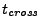 , the ray's cell crossing time.
, the ray's cell crossing time.
The AVG algorithm, while conceptually simple, leads to discontinous change in 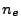 at the
cell interfaces. To account for this,
the ray undergoes refraction according to Snell's law. Refraction at cell interfaces causes a
change in the ray's velocity normal to the interface surface while preserving the ray velocity
component transverse to the interface normal. To derive the change in the ray normal velocity
component, imagine the cell interface to have a small infinitesimal thickness
at the
cell interfaces. To account for this,
the ray undergoes refraction according to Snell's law. Refraction at cell interfaces causes a
change in the ray's velocity normal to the interface surface while preserving the ray velocity
component transverse to the interface normal. To derive the change in the ray normal velocity
component, imagine the cell interface to have a small infinitesimal thickness 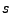 and the ray moving
from left to right through the interface. On the left and right the normal velocity components are
and the ray moving
from left to right through the interface. On the left and right the normal velocity components are
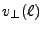 and
and 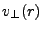 , respectively, while the corresponding
, respectively, while the corresponding 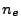 are
are 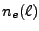 and
and 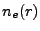 .
Since we are dealing with an interface of infinitesimal thickness, we can use the first order
equation 18.40 to get
.
Since we are dealing with an interface of infinitesimal thickness, we can use the first order
equation 18.40 to get
where
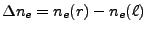 , and the electron number density gradient is
, and the electron number density gradient is
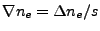 .
But
.
But 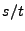 is the average velocity of the ray passing through the interface and since we
have constant acceleration we have
is the average velocity of the ray passing through the interface and since we
have constant acceleration we have
![$ s/t=[v_\bot(r)+v_\bot(\ell)]/2$](img1230.png) , which, when inserted into
the last equation, gives
, which, when inserted into
the last equation, gives
Clearly there is a limit as to how large
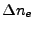 can be for refraction to occur. If
can be for refraction to occur. If
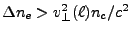 , we have
, we have
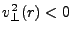 , which is impossible. The
only way out is then for the ray to have
, which is impossible. The
only way out is then for the ray to have
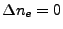 , i.e. the ray stays in the same cell
and reflects with
, i.e. the ray stays in the same cell
and reflects with
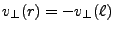 .
.
The basic algorithmic steps for tracing a single ray through all cells in one block
(see Figure 18.4) can be summarized as follows:
Figure 18.4:
A single ray crossing a cell.
|
|
The initial situation has the ray positioned on one of the block's faces with velocity components such
that the ray's direction of movement is into the block.
- Identify ray entry cell
 , entry position
, entry position  , entry velocity
, entry velocity 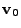 and entry
power
and entry
power 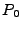 .
.
- Calculate
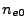 and
and 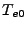 at the entry point using equations 18.62 and 18.63.
at the entry point using equations 18.62 and 18.63.
- Solve equation 18.41 for time for each possible cell face. Identify the cell
crossing time
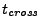 as minimum of all solutions
as minimum of all solutions 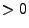 .
.
- Using
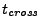 and equation 18.41 again, find the cell exit position
and equation 18.41 again, find the cell exit position
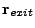 .
.
- Calculate
![$ \ln \Lambda[{\bf r}_0]$](img1245.png) ,
,
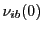 ,
, 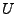 ,
, 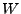 ,
, 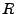 ,
, 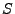 and evaluate
and evaluate 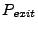 using equations
18.47 and 18.59.
using equations
18.47 and 18.59.
- Using
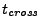 and equation 18.40, find the ray's exit velocity
and equation 18.40, find the ray's exit velocity
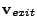 .
.
- Based on
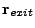 and
and
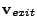 determine new entry cell
determine new entry cell 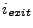 .
.
- Calculate the electron number density jump
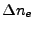 between both cells
between both cells 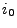 and
and 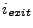 , using
equation 18.39.
, using
equation 18.39.
- Check for reflection or refraction using Snell's law equation 18.67 and update
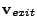 and possibly new entry cell
and possibly new entry cell 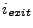 .
.
- If cell
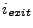 is still in block, set all exit variables equal to entry variables and
repeat the steps.
is still in block, set all exit variables equal to entry variables and
repeat the steps.
18.4.4.2 Cubic Interpolation with Piecewise Parabolic Ray Tracing (CIPPRT)
The use of cubic interpolation schemes is an attempt at providing continuous 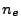 and
and 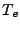 representations as
well as continuous first derivatives
representations as
well as continuous first derivatives
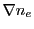 and
and
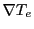 throughout the entire domain. This allows
for the calculation of a more smoother path for each ray inside each cell when compared to the AVG algorithm.
In effect, the cell-by-cell choppiness of the AVG algorithm can be avoided by taking many small ray
steps inside each cell. Also, the troublesome
throughout the entire domain. This allows
for the calculation of a more smoother path for each ray inside each cell when compared to the AVG algorithm.
In effect, the cell-by-cell choppiness of the AVG algorithm can be avoided by taking many small ray
steps inside each cell. Also, the troublesome 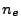 discontinuities at the cell boundaries and the
application of Snell's law will disappear. The essential features of the cubic interpolation schemes are
layed out in section 32.2. In what follows we show the piecewise parabolic ray tracing scheme.
discontinuities at the cell boundaries and the
application of Snell's law will disappear. The essential features of the cubic interpolation schemes are
layed out in section 32.2. In what follows we show the piecewise parabolic ray tracing scheme.
The CIPPRT algorithm tries to map out the ray path inside each cell as a sequence of parabolic
(i.e. constant acceleration) paths. It resembles the AVG algorithm and uses the same equations
Eq.(18.40) and Eq.(18.41) for determination of velocity and position
of each parabolic section of the path. The main difference between the AVG and the CIPPRT is that
the latter uses the cubic interpolated ray acceleration field at each cell point, whereas the former
assumes the same constant acceleration at each point throughout the cell. The CIPPRT can hence be viewed as a
succession of AVG steps inside each cell. The energy deposition of each parabolic path section
is also calculated like for the AVG algorithm, namely solving the exponential time integral
in Eq.(18.47) using the second order Gaussian quadrature in Eq.(18.59).
The required 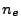 and
and 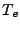 at the Gaussian quadrature points are evaluated using the cubic interpolation
equation Eq.(32.11). The following scheme illustrates the steps involved for tracing a
ray through a cell, assuming the ray is somewhere located in the cell at
at the Gaussian quadrature points are evaluated using the cubic interpolation
equation Eq.(32.11). The following scheme illustrates the steps involved for tracing a
ray through a cell, assuming the ray is somewhere located in the cell at 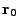 with velocity
with velocity 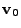 :
:
- Calculate, using Eq.(32.13), the electron number density gradient
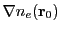 .
.
- Determine the time
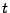 to reach the next cell face using the quadratic time equation
Eq.(18.41) and determine the ray's position
to reach the next cell face using the quadratic time equation
Eq.(18.41) and determine the ray's position
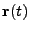 on the face.
on the face.
- Do two
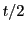 steps and calculate the
steps and calculate the
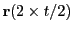 position. The first
position. The first 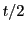 step is
guaranteed to stay inside the cell. Hence
step is
guaranteed to stay inside the cell. Hence
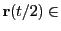 cell. However, despite
cell. However, despite
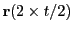 having the potential to step outside the cell, we only need it for
comparison with
having the potential to step outside the cell, we only need it for
comparison with
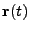 .
.
- Form the error vector
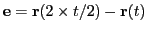 . If
. If
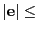 target
accuracy, accept the
target
accuracy, accept the
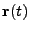 position. If not, set
position. If not, set 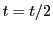 and repeat step 2).
and repeat step 2).
- Once a satisfactory stepping time has been determined, update the velocity using
Eq.(18.40).
18.4.4.3 Cubic Interpolation with Runge Kutta Integration (CIRK)
Instead of using the piecewise parabolic ray tracing approach, the CIRK algorithm advances the ray through
cells using Runge Kutta (RK) integration 34.2. An advantage of using the RK integrator is
that the rate of power loss ODE 18.42 can be directly incorporated into the
RK solution vector, thereby gaining access over its error control. The ray tracing RK vector has 7 entries
and the independent variable 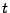 does not appear on the rhs. Since each ray must be traced on a cell-by-cell
basis, we have to make sure that each RK step either stays within the cell or hits one of its walls. The CIRK
algorithm therefore has to use the confined RK stepping routine.
does not appear on the rhs. Since each ray must be traced on a cell-by-cell
basis, we have to make sure that each RK step either stays within the cell or hits one of its walls. The CIRK
algorithm therefore has to use the confined RK stepping routine.
18.4.5 Setting up the Laser Pulse
The laser's pulse contains information about the laser's energy profile and can thus be characterized by a
function of laser power in terms of time 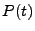 . The curve of
. The curve of 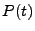 gives the power of the laser pulse
at any given simulation time. In FLASH, the form of
gives the power of the laser pulse
at any given simulation time. In FLASH, the form of 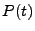 is given by a series of points, which are
connected via straight lines (see Figure 18.5).
is given by a series of points, which are
connected via straight lines (see Figure 18.5).
Figure 18.5:
The structure of the laser pulse.
|
|
Each point denotes a power/time pair 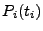 . The average laser power
. The average laser power
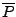 of the pulse
during a time step from
of the pulse
during a time step from
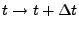 is then
is then
where the integration is performed piecewise between all the points 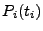 contained within
the relevant time frame. The average laser power will be distributed among all the rays that
will be created during that particular time step. Note, that
contained within
the relevant time frame. The average laser power will be distributed among all the rays that
will be created during that particular time step. Note, that 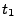 is the time the laser first comes
into existence. In Figure 18.5 there is therefore no line connecting the origin (zero power)
with
is the time the laser first comes
into existence. In Figure 18.5 there is therefore no line connecting the origin (zero power)
with 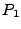 . If the user wants a gradual buildup of laser power from zero, an explicit point
. If the user wants a gradual buildup of laser power from zero, an explicit point 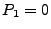 must be given at time
must be given at time 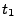 . The same consideration applies for the other end of the timescale.
. The same consideration applies for the other end of the timescale.
18.4.6 Setting up the Laser Beam
The laser's beam contains all the information about orientation and shape of the laser. The orientation
is characterized by specifying lens and target coordinates. The shape of the laser is given by the
size and shape of the lens and target cross section areas and the
cross-sectional ray power distribution law. Figure 18.6 is helpful in
visualizing the position of the vectors for the formulas below.
Figure 18.6:
The laser beam.
|
|
The most important vectors for setting up the rays are the two local elliptical semiaxes unit vectors
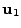 and
and 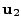 . These two unit vectors, together with the lens and target positions,
are very convenient in calculating the rays lens and target coordinates. Note, that the unit vectors
are the same for both the lens and the target, if defined from their corresponding local elliptical
centers. In what follows, vectors in capital letters are defined in the global coordinate system and
vectors in small letters are defined in the local target coordinate system.
. These two unit vectors, together with the lens and target positions,
are very convenient in calculating the rays lens and target coordinates. Note, that the unit vectors
are the same for both the lens and the target, if defined from their corresponding local elliptical
centers. In what follows, vectors in capital letters are defined in the global coordinate system and
vectors in small letters are defined in the local target coordinate system.
The laser beam originates at the lens, whose center is located at  , and hits the target,
whose center is located at
, and hits the target,
whose center is located at  . In 3D geometries, the elliptical target area is defined as
an ellipse perpendicular to the lens-target line and whose largest semiaxis
. In 3D geometries, the elliptical target area is defined as
an ellipse perpendicular to the lens-target line and whose largest semiaxis  is positioned
such that it makes a torsional angle
is positioned
such that it makes a torsional angle 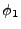 with the local target z-axis (see Figure 18.6).
Let us define the beam vector
with the local target z-axis (see Figure 18.6).
Let us define the beam vector
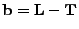 pointing from the target to the lens
and connecting the two respective centers. We then have the defining equations
for
pointing from the target to the lens
and connecting the two respective centers. We then have the defining equations
for 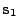
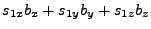 |
 |
0 |
(18.70) |
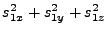 |
 |
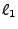 |
(18.71) |
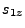 |
 |
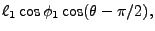 |
(18.72) |
where 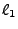 is the length of
is the length of 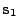 and
and 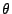 is the angle that the beam
vector
is the angle that the beam
vector 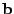 makes with the local z-axis. The first equation 18.70 says
that
makes with the local z-axis. The first equation 18.70 says
that 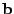 and
and 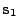 are orthogonal. The second one 18.71 defines
the length of
are orthogonal. The second one 18.71 defines
the length of 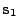 and the third one 18.72 defines the local z-axis
projection of
and the third one 18.72 defines the local z-axis
projection of 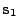 . The last equation can be rewritten as
. The last equation can be rewritten as
Forming an expression for 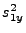 from equation 18.70, an expression for
from equation 18.70, an expression for
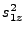 from equation 18.72 and inserting the results into equation
18.71, we obtain a quadratic equation in
from equation 18.72 and inserting the results into equation
18.71, we obtain a quadratic equation in 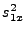 , from which we can
obtain all three components. We get after some algebra and simplifications
, from which we can
obtain all three components. We get after some algebra and simplifications
The two possible solutions for 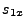 and
and 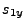 correspond to the two
possible definitions of the rotation angle
correspond to the two
possible definitions of the rotation angle 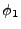 in either clockwise or
counterclockwise rotation from the z-axis when looking along the beam vector
in either clockwise or
counterclockwise rotation from the z-axis when looking along the beam vector
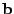 from the lens to the target. Let us henceforth define
from the lens to the target. Let us henceforth define 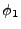 to be the clockwise rotation. Then the lower signs in
to be the clockwise rotation. Then the lower signs in 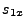 and
and 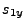 apply and dividing each component by
apply and dividing each component by 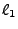 we obtain for the unit vector
components
we obtain for the unit vector
components
The second elliptical semiaxis 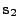 is perpendicular to the
first and lays in the same elliptical target plane. If we define it to
be at a right angle in clockwise direction from
is perpendicular to the
first and lays in the same elliptical target plane. If we define it to
be at a right angle in clockwise direction from 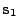 , the torsional angle
it makes with the local z-axis is
, the torsional angle
it makes with the local z-axis is
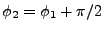 . The formulas for
its unit vector components are the same as for
. The formulas for
its unit vector components are the same as for 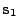 but with
but with 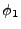 replaced
by
replaced
by 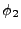 . From trigonometric sine and cosine relations we can re-express them in terms
of
. From trigonometric sine and cosine relations we can re-express them in terms
of 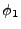
Note the importance of the
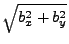 term. If this term is equal
to zero, then the unit vectors become undefined. This corresponds to the laser beam
being parallel to the global z-axis (and thus coinciding with the local z-axis). Then
both elliptical semiaxes are not defined uniquely through a z-axis torsional angle of
zero. In this case the torsional angle must be defined through one of the other
coordinate axis. The following coordinate index permutations in the above formulas apply:
term. If this term is equal
to zero, then the unit vectors become undefined. This corresponds to the laser beam
being parallel to the global z-axis (and thus coinciding with the local z-axis). Then
both elliptical semiaxes are not defined uniquely through a z-axis torsional angle of
zero. In this case the torsional angle must be defined through one of the other
coordinate axis. The following coordinate index permutations in the above formulas apply:
In 2D geometries, the beam's lens and target areas shrink to a line segment. All z-components
are zero and the torsional angle is equal to 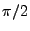 . The components of the unit vector
can be deduced from the equations 18.77 and 18.78 as
. The components of the unit vector
can be deduced from the equations 18.77 and 18.78 as
18.4.6.2 Extremum Values for the Elliptical Target Zone
In 3D simulations, the planar elliptical target zone can be placed in any possible
way inside the domain by specifying the lens 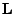 and target
and target 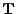 positions, both
elliptical target zone semiaxes lengths
positions, both
elliptical target zone semiaxes lengths 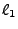 and
and 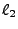 , the first semiaxis torsion
angle
, the first semiaxis torsion
angle 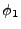 and the coordinate axis to which
and the coordinate axis to which 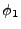 refers to. We wish to enforce in the
code a complete containment of the entire target plane inside the domain boundaries. To check
this condition we need the extremum coordinate values of the elliptical boundary curve of the
target. The collection of all points
refers to. We wish to enforce in the
code a complete containment of the entire target plane inside the domain boundaries. To check
this condition we need the extremum coordinate values of the elliptical boundary curve of the
target. The collection of all points 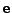 , based on the local target coordinate system,
can be given in the following implicit form
, based on the local target coordinate system,
can be given in the following implicit form
Differentiating with respect to 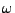 and equating to zero we get the minimax condition
on all coordinate components as
and equating to zero we get the minimax condition
on all coordinate components as
where
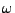
 denotes the vector of the minimax angles for each cartesian component.
The equation 18.88 has two possible answers for each
denotes the vector of the minimax angles for each cartesian component.
The equation 18.88 has two possible answers for each 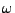 component in the
range
component in the
range
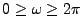 , corresponding to the minimum and the maximum value.
The
, corresponding to the minimum and the maximum value.
The
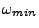 and
and
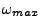 angles differ by
angles differ by 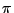 radians for each cartesian component.
The corresponding minima and maxima on the elliptical boundary curve are obtained
by inserting the
radians for each cartesian component.
The corresponding minima and maxima on the elliptical boundary curve are obtained
by inserting the
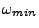 and
and
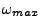 angles into equation 18.87.
angles into equation 18.87.
In order to simplify things, we note that what we need are the sine and cosine values
of
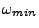 and
and
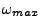 . From the definition of the trigonometric functions based
on the length of the three sides of a right-angled triangle (a = opposite side, b =
adjacent side, c = hypotenuse for an angle
. From the definition of the trigonometric functions based
on the length of the three sides of a right-angled triangle (a = opposite side, b =
adjacent side, c = hypotenuse for an angle 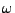 ), we have, using
), we have, using
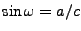 ,
,
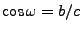 ,
,
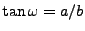 and
and
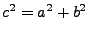
When applied to equation 18.87, we obtain
The corresponding minimax equation for the 2D geometries (ellipse
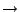 line segment)
is
line segment)
is
with  being half the length of the target line segment and
being half the length of the target line segment and 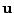 the line segment unit
vector.
the line segment unit
vector.
18.4.7 Setting up the Rays
For each Energy Deposition unit call, the code sets up the initial collection of rays, defined
to be located on the domain boundary with specific velocity components such that they will hit
the target area at precise locations if they would cross an empty domain. Key concepts in setting
up the rays initial position, velocity and power are the elliptical local square, radial, delta or
statistical grids and the beam cross section power function. Rays will be launched from the lens
grid intersection points to the corresponding target grid intersection points.
Figure 18.7:
Setting up the rays between the beam's lens and target area using
a square grid. Only half of the square elliptical grids are shown for clarity.
|
|
Using a square grid, a uniform beam cross-sectional ray density will be achieved, although
this could be relaxed in the future to include the possibility of rectangular grids leading to different
cross-sectional ray densities along the two elliptical semiaxes directions. A radial grid
places the rays on concentrical ellipses.
18.4.7.1 The Elliptical Lens/Target Local Square Grid
In 3D geometries, both the lens and target areas are defined as two similar ellipses (different size,
same shape). Given a specific elliptical shape by defining the lengths of both semiaxes
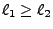 ,
we can set up a square grid inside the ellipse, such that the number of grid intersection
points matches closely the number of rays
,
we can set up a square grid inside the ellipse, such that the number of grid intersection
points matches closely the number of rays 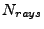 specified by the user. The grid is defined by
the separation
specified by the user. The grid is defined by
the separation 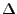 between two grid points and the placement of the grid's origin at the
center of the ellipse. Our goal is to find this
between two grid points and the placement of the grid's origin at the
center of the ellipse. Our goal is to find this 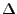 value.
value.
Denote by
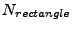 the number of grid intersection points for the circumscribing rectangle with
sides
the number of grid intersection points for the circumscribing rectangle with
sides 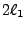 and
and 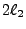 . We then have
. We then have
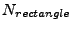 |
 |
Number of ellipse points |
|
| |
 |
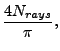 |
(18.93) |
this relation holding only approximately due to the finite resolution of the grid. Let us denote
by
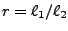 the ratio between the largest and smallest semiaxis. If
the ratio between the largest and smallest semiaxis. If 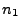 is the number of
tics along the
is the number of
tics along the 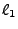 -semiaxis starting at the grid origin (0,0), then the number of tics along the
-semiaxis starting at the grid origin (0,0), then the number of tics along the
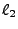 -semiaxis is approximately equal to
-semiaxis is approximately equal to 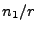 . Looking at the circumscribed rectangle area, the
total number of grid intersection points laying on the grid's axes will be twice those on each
semiaxis plus the grid's origin:
. Looking at the circumscribed rectangle area, the
total number of grid intersection points laying on the grid's axes will be twice those on each
semiaxis plus the grid's origin:
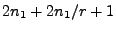 . The total number of grid intersection points
not on any of the axes is
. The total number of grid intersection points
not on any of the axes is
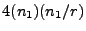 . Both numbers together should then equal to
. Both numbers together should then equal to
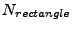 .
Hence, from 18.93, we are lead to a quadratic equation in
.
Hence, from 18.93, we are lead to a quadratic equation in 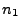
whose solution is
Always 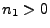 , which can easily be seen from the lowest possible value that
, which can easily be seen from the lowest possible value that 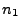 can attain for
can attain for
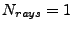 and the lowest possible ratio
and the lowest possible ratio 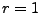 (in this case
(in this case
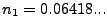 ). Since
). Since 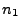 has to
be an integer we take the ceiling value of the solution 18.95. If the user
specified
has to
be an integer we take the ceiling value of the solution 18.95. If the user
specified
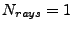 , the search for
, the search for 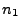 is bypassed and the ray is placed at the elliptical origin.
is bypassed and the ray is placed at the elliptical origin.
Having 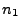 , the next task is to find the optimum (or close to optimum) grid spacing
, the next task is to find the optimum (or close to optimum) grid spacing 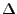 . This
is done by defining a minimum and maximum grid spacing value
. This
is done by defining a minimum and maximum grid spacing value
A series of
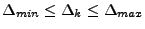 grid spacings is then tested, and for each
grid spacings is then tested, and for each
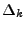 the number of grid intersection points
the number of grid intersection points 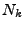 inside the ellipse area is determined. Of all
inside the ellipse area is determined. Of all
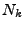 obtained, a certain number of them will be closest to
obtained, a certain number of them will be closest to 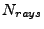 . The average over all these
. The average over all these
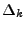 will then be taken as the final
will then be taken as the final 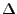 value. For this
value. For this 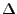 we compute
the final number of grid intersection points, which will then replace the user's specified
we compute
the final number of grid intersection points, which will then replace the user's specified 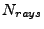 .
.
Since the target 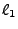 and
and 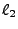 semiaxes are specified by the user, the
semiaxes are specified by the user, the 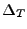 for
the target square grid is evaluated using the above algorithm. The corresponding lens
for
the target square grid is evaluated using the above algorithm. The corresponding lens 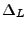 value is set using the similarity in size between the lens and the target. Using the user's
specified
value is set using the similarity in size between the lens and the target. Using the user's
specified 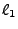 for the lens, the preservation of length relations between similar objects
leads to:
for the lens, the preservation of length relations between similar objects
leads to:
and hence
In 2D geometries the situation is much simpler. Due to the linear shape of the lens and target areas,
it is very easy to calculate the 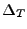 value of the linear target grid such that exactly
value of the linear target grid such that exactly
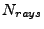 grid points are obtained with the outer two grid points coinciding with the target end points.
The corresponding
grid points are obtained with the outer two grid points coinciding with the target end points.
The corresponding 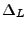 is evaluated using equation 18.99.
is evaluated using equation 18.99.
18.4.7.2 The Elliptical Lens/Target Local Radial Grid
In order to set up the radial lens and target grids, we use the implicit definition of the elliptical curve
from 18.87. The grid will then be defined as the number of tics on the
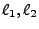 pair and the number of tics on the angle
pair and the number of tics on the angle 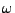 within the range
within the range
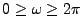 . The number
of tics on both of these 'axes' will be the same and will be denoted by
. The number
of tics on both of these 'axes' will be the same and will be denoted by 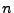 . The total number of radial
grid points within the lens and target ellipses will be equal to
. The total number of radial
grid points within the lens and target ellipses will be equal to 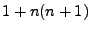 , leading to the quadratic
equation
, leading to the quadratic
equation
whose relevant solution is
In order to reduce the error to 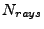 , rounding to the nearest integer is applied for
, rounding to the nearest integer is applied for 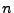 . The
individual grid points are calculated from
. The
individual grid points are calculated from
where the index ranges are
In an effort to provide more control to the user, the default 'same number of tics on both radial and
angular axes' has been extended, such that the user can enforce one or even both of these values.
This is controlled by setting the requested number of radial and/or angular tics as runtime parameters
for each beam. The resulting number of rays will then be recalculated and overwritten.
18.4.7.3 The Elliptical Lens/Target Local Delta Grid
One of the drawbacks of the local square grid is that the user has no direct control of the resulting
tic separation. The main goal when setting up the local square grid is to have the number of rays
match as closely as possible the number of rays requested by the user. The local delta grid is provided
to give the user full control over the tic separations on both semiaxes, relaxing at the same time
the number of rays constraint. The delta grid becomes useful if the user wants to enforce a more
smooth energy deposition in the cells hit by the 3D laser beam. Rays can be forced to hit each cell
well away from the cell boundary, thereby avoiding the initial uneven ray distributions due to some rays
hitting the block walls with corresponding nudging to one block or the other. As a consequence the delta
grids are most useful if the target area of the beam has or is known to have a uniform refinement level.
The setup of the delta grid is simple: the user has to provide the tic separation values as beam runtime
parameters. The beam setup code then adheres strictly to these values and excludes any grid points laying
outside the elliptical beam boundary. The number of rays requested initially by the user is completely
ignored and replaced by the number of rays determined for the delta grid. The user must make sure
that the supplied memory requirements for ray storage are ok. This can be done by estimating the number
of rays resulting from the delta grid on the area of the circumscribed rectangle with sides 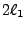 and
and
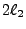 and rescaling by the ellipse/rectangle area factor. If we denote the user supplied tic separations
corresponding to the
and rescaling by the ellipse/rectangle area factor. If we denote the user supplied tic separations
corresponding to the 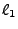 semiaxis and
semiaxis and 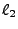 semiaxis by
semiaxis by 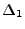 and
and 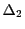 , then the
estmated number of rays would be:
, then the
estmated number of rays would be:
The first tics of the delta grid along each grid axis start at
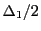 and
and
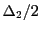 . The grid center
. The grid center
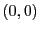 is thus not part of the delta grid.
is thus not part of the delta grid.
18.4.7.4 The Elliptical Lens/Target Local Statistical Grid
The local statistical grid is defined by a statistical collection of 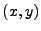 pairs within the
range
pairs within the
range ![$ [-1,1]$](img1396.png) , where the
, where the  and
and  denote fractions of the
denote fractions of the 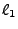 and
and 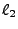 semiaxis. A
random number generator for the range
semiaxis. A
random number generator for the range ![$ [0,1]$](img1397.png) is used and the numbers are shifted to the
is used and the numbers are shifted to the
![$ [-1,1]$](img1396.png) range by multiplying by 2 and adding
range by multiplying by 2 and adding 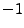 . Every
. Every 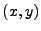 pair is checked, if it actually
lays within the ellipse and retained if it does. The random
pair is checked, if it actually
lays within the ellipse and retained if it does. The random 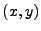 pair generation stops,
once the requested number of rays is reached. In order to use different statistical grids
for each time step, the statistical grid is regenerated afresh for each time step using a different
random seed value.
pair generation stops,
once the requested number of rays is reached. In order to use different statistical grids
for each time step, the statistical grid is regenerated afresh for each time step using a different
random seed value.
18.4.7.5 Beam Cross Section Power Function
The beam cross section power function describes the power distribution of the rays inside the beam
at launching time. Currently there are two types of power distribution functions implemented in FLASH:
1) uniform (flat) distribution (equal power) and 2) gaussian decay from the center of the beam.
The first one is trivial: every ray gets assigned an equal amount of power. The gaussian decay function assigns
to each ray a relative weight according to the position inside the elliptical cross section of the beam.
Using the local  and
and  target coordinate system located at the center of the beam, the
gaussian weighting function for 2D target areas (3D geometries) reads
target coordinate system located at the center of the beam, the
gaussian weighting function for 2D target areas (3D geometries) reads
where  and
and  denote the local coordinates inside the ellipse along the
denote the local coordinates inside the ellipse along the 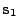 and
and 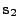 axes, respectively,
axes, respectively, 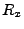 and
and 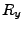 are user defined decay radii values and
are user defined decay radii values and 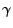 is the user defined
gaussian super exponent. For 1D target areas (2D geometries) the weighting function is
is the user defined
gaussian super exponent. For 1D target areas (2D geometries) the weighting function is
In order to determine the actual power assigned to each ray, we use the average laser power from
equation 18.69
The sum of the weights over all rays plays the role of a sort of partition function for the beam
grid and can thus be precomputed and become part of the beam properties when setting up the beams.
18.4.7.6 The Rays Initial Position and Velocity
In 3D, after the local lens and target grids have been set up, each ray has associated with it
a local lens elliptical coordinate pair 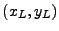 and a local target elliptical coordinate pair
and a local target elliptical coordinate pair 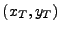 .
The corresponding global coordinates can be obtained using the global lens and target center
coordinates and the elliptical unit vectors (see Figure 18.7)
.
The corresponding global coordinates can be obtained using the global lens and target center
coordinates and the elliptical unit vectors (see Figure 18.7)
Defining now the ray vector 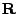 pointing from the lens to the target
pointing from the lens to the target
we can state the parametric ray line equation
The ray line equation is used to determine where and which domain boundary surface the ray will
hit. Consider a domain boundary surface contained within a plane given by the equation
The value of the real 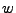 parameter where the ray line meets this plane is obtained by inserting
the ray line equation into the plane equation. It is
parameter where the ray line meets this plane is obtained by inserting
the ray line equation into the plane equation. It is
Inserting this 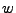 value into the ray line equation 18.112 we obtain the
location
value into the ray line equation 18.112 we obtain the
location
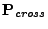 of the crossing point on the plane. From Figure 18.7, for the
ray vector to cross the plane, the value of
of the crossing point on the plane. From Figure 18.7, for the
ray vector to cross the plane, the value of 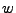 must be in the range
must be in the range
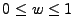 . A value of
. A value of 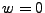 or
or 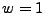 indicates that the plane is crossing the lens or target area, respectively. If
indicates that the plane is crossing the lens or target area, respectively. If 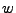 is in
proper range, it must next be checked if
is in
proper range, it must next be checked if
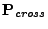 is located within the domain boundary
surface. If yes, that
is located within the domain boundary
surface. If yes, that 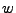 value is accepted. Note, that several proper
value is accepted. Note, that several proper 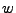 values can be
obtained. A ray crossing near the corner of a rectangular domain gives three proper
values can be
obtained. A ray crossing near the corner of a rectangular domain gives three proper 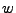 values
corresponding to crossing the three rectangular planes defining the corner. Since the rays
originate from the lens, the relevant
values
corresponding to crossing the three rectangular planes defining the corner. Since the rays
originate from the lens, the relevant 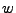 is the one with minimum value and the corresponding
is the one with minimum value and the corresponding
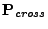 will be taken as the rays initial position. The initial ray velocity components
are determined from the unit vector of the ray vector
will be taken as the rays initial position. The initial ray velocity components
are determined from the unit vector of the ray vector
where 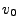 is the initial magnitude of the velocity (in most simulations this is the speed
of light). For 2D geometries all the above equations remain the same, except for the ray global
coordinates, for which the terms in
is the initial magnitude of the velocity (in most simulations this is the speed
of light). For 2D geometries all the above equations remain the same, except for the ray global
coordinates, for which the terms in 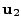 are dropped and for the domain boundary planes, for which
the terms involving the z-component in the defining equation 18.113 do not exist.
The following steps summarize the determination of the initial ray positions and
velocity components for each ray:
are dropped and for the domain boundary planes, for which
the terms involving the z-component in the defining equation 18.113 do not exist.
The following steps summarize the determination of the initial ray positions and
velocity components for each ray:
- Form the ray vector
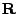 using 18.111.
using 18.111.
- Find the collection
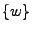 of all
of all
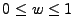 values using 18.114 for all
domain surface planes (
values using 18.114 for all
domain surface planes (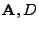 ).
).
- Using the ray line equation 18.112, remove all
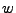 values from
values from 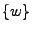 which
lead to plane crossing points
which
lead to plane crossing points
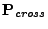 not contained within the domain boundary surface.
not contained within the domain boundary surface.
- Take the minimum of the remaining
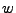 's in
's in 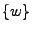 and calculate the corresponding
and calculate the corresponding
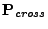 .
This is the ray's initial position vector.
.
This is the ray's initial position vector.
- Using the ray vector
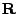 again calculate the velocity components using 18.115.
again calculate the velocity components using 18.115.
18.4.8 3D Laser Ray Tracing in 2D Cylindrical Symmetry
Performing a pure 2D cylindrical ray tracing has an obvious disadvantage: each ray must also
be treated as a 2D cylindrical symmetrical object. Each ray can only hit the R-disk of the cylindrical
domain at precisely 90 degrees and no variation in this incident angle is possible. However, if
one treats the cylinder as a true 3D object, then it is possible to trace each ray through this
3D cylinder. The advantage of retaining the 2D cylindrical description of the domain is obvious:
only 2D storage is needed to describe the properties of the domain.
Figure 18.8:
Tracing a ray in 3D in a 2D cylindrical domain.
View onto the R-disk. The z-axis has been left out for clarity.
|
|
3D in 2D ray tracing is much more complicated than either the simple pure 3D or pure 2D counterparts.
The interplay between the polar and the cartesian coordinates leads to ray tracing equations which
can only be solved approximately via the use of elliptical integrals. Rather than approximating the
integrals involved, a second approach decomposes the 3D cylinder into several identical cylindrical
wedges with each wedge having planar boundaries. The larger the number of wedges the more accurate
the 3D in 2D ray tracing will be. Both approaches (approximating the integrals and wedging the 3D
cylinder) are entirely equivalent.
We will first state the exact time-radial solution of an object of mass  moving in a central force
environment with no external forces acting on it. The motion of such an object is characterized by
constant energy and angular momentum and is hence confined to a 2D plane. There are two ways to describe the position
moving in a central force
environment with no external forces acting on it. The motion of such an object is characterized by
constant energy and angular momentum and is hence confined to a 2D plane. There are two ways to describe the position
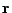 , velocity
, velocity 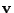 and acceleration
and acceleration 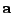 vectors of a particle in a 2D plane: using cartesian
vectors of a particle in a 2D plane: using cartesian
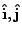 or polar
or polar
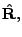
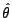 unit vectors.
They are interrelated by
unit vectors.
They are interrelated by
Using these unit vectors and the differentiation chain rule we get
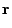 |
 |
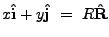 |
(18.117) |
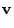 |
 |
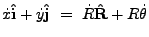 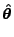 |
(18.118) |
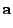 |
 |
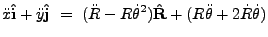 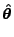 |
(18.119) |
where each dot on the dotted variables stands for 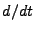 . The angular momentum of the object in
polar coordinates is
. The angular momentum of the object in
polar coordinates is
and its magnitude
Since only a central force component is present, this force depends only on the radial part
We are now ready to state the equation of motion of the object in polar coordinates. Let's assume
the object has initially at time 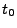 the coordinates (
the coordinates (
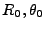 ), and let
), and let 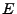 be its constant energy.
be its constant energy.
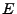 is composed of two parts: kinetic and potential energy. Both parts will change as time passes by.
The potential energy
is composed of two parts: kinetic and potential energy. Both parts will change as time passes by.
The potential energy 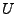 can only change along a change in
can only change along a change in 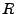 , because the force has only a radial component.
We have
, because the force has only a radial component.
We have
where in the last step we have eliminated the angular dependence through the use of
Eq. (18.121). The last equation for  is a first order
differential equation allowing for separation of variables
is a first order
differential equation allowing for separation of variables
The potential energy can be obtained via integration
The value of the initial potential energy is arbitrary and is conveniently set to zero. Assuming
further that  , we obtain
, we obtain
Given an initial radial  and a final target radial
and a final target radial  value,
value, 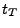 is the time the object will
take in travelling from
is the time the object will
take in travelling from 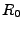 to
to 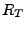 under the specified initial conditions at
under the specified initial conditions at 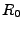 (values of
(values of 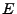 and
and 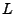 ).
If the object will not reach
).
If the object will not reach 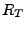 then
then 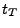 is either negative or complex. The time equation
(18.126) can be solved analytically only for a small number of cases (like
for example if
is either negative or complex. The time equation
(18.126) can be solved analytically only for a small number of cases (like
for example if 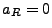 ). All other cases require numerical approximation to the radial integral.
For our case, when the ray moves through one radial 2D cylindrical zone using the AVG approximation
18.4.4.1, the central force acceleration is constant, i.e
). All other cases require numerical approximation to the radial integral.
For our case, when the ray moves through one radial 2D cylindrical zone using the AVG approximation
18.4.4.1, the central force acceleration is constant, i.e 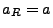 . For this case we have
. For this case we have
for which it is possible to give an analytical solution in terms of elliptical integrals. However,
the analytical solution is far to complicated to be of practical use.
The main reason for the complicated time equation has its roots in the 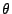 polar variable
describing the rotational symmetry. An approximate treatment can be formulated, in which
each circle is treated as a linear polygon with
polar variable
describing the rotational symmetry. An approximate treatment can be formulated, in which
each circle is treated as a linear polygon with 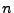 sides (
sides (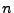 not necessarily integer), where
the value of
not necessarily integer), where
the value of 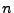 determines the quality of the approximation. The exact 3D radial acceleration cylindrical
problem in
determines the quality of the approximation. The exact 3D radial acceleration cylindrical
problem in
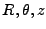 coordinates is transformed into an approximate 3D cartesian problem in
coordinates is transformed into an approximate 3D cartesian problem in
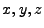 coordinates, where the
coordinates, where the 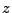 coordinate remains unaffected. Each torus cell is hence
approximated as a collection of truncated wedge (TW) cells. The trapezoidal sides of these wedges
are parallel to the
coordinate remains unaffected. Each torus cell is hence
approximated as a collection of truncated wedge (TW) cells. The trapezoidal sides of these wedges
are parallel to the 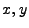 plane and the rectangular sides are perpendicular to this plane.
Since all TW cells have exactly the same size and shape when coming from the same torus cell, it
suffices to concentrate on just one of them. These representative TW cells will be placed inside the
plane and the rectangular sides are perpendicular to this plane.
Since all TW cells have exactly the same size and shape when coming from the same torus cell, it
suffices to concentrate on just one of them. These representative TW cells will be placed inside the
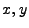 plane, such that the positive
plane, such that the positive  axis divides the trapezoidal sides into two equal areas.
The collection of all representative TW cells has the shape of a wedge with opening angle
axis divides the trapezoidal sides into two equal areas.
The collection of all representative TW cells has the shape of a wedge with opening angle 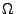 .
.
Figure 18.9:
Shape and location of the TW cells.
|
|
In order to trace the rays through the TW cells, we need the equation of all the cell boundary planes.
The equations of the cell planes perpendicular to the 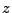 axis (containing the trapezoidal sides)
are simply
axis (containing the trapezoidal sides)
are simply
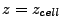 . The equations of the cell planes perpendicular to the
. The equations of the cell planes perpendicular to the  axis are similarly
axis are similarly
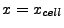 . The remaining cell plane equations corresponding to the non-coplanar cell faces are
(see Figure 18.9)
. The remaining cell plane equations corresponding to the non-coplanar cell faces are
(see Figure 18.9)
The quadratic time equations to be solved for the
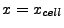 and
and
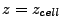 plane equations are
of the same form as equation 18.65. For the plane equations in
18.128 we obtain, after inserting the appropriate forms into
the general cartesian quadratic time equation 18.64 and considering
the zero gradient approximation in
plane equations are
of the same form as equation 18.65. For the plane equations in
18.128 we obtain, after inserting the appropriate forms into
the general cartesian quadratic time equation 18.64 and considering
the zero gradient approximation in  direction
direction
![$\displaystyle -\frac{c^2}{4n_c}\left[\mp m{\langle\nabla n_e\rangle}_x\right]t^2
+\left[\mp mv_{0x}+v_{0y}\right]t
+\left[\mp mr_{0x}+r_{0y}\right]$](img1476.png) |
 |
0 |
(18.129) |
We now describe the three main tasks for the 3D in 2D ray tracing: 1) proper setup of lenses and
corresponding targets, 2) initial placement of the 3D rays on the 2D cylindrical domain and 3)
tracing of the rays through the truncated wedges.
18.4.8.3 Extremum Global Radial 3D and 2D Distance Values for 3D Elliptical Lens and Target Zones
In curved domain setups (cylindrical and spherical), it becomes necessary to calculate
extremum global radial distance values for a 3D elliptical curve from the domain origin in order
to check proper placements of the lens and target zones. We start by stating the global equation
of the elliptical target curve 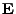 (the treatment of the lens ellipse is analogous) in 3D
in implicit form (see Figure 18.6):
(the treatment of the lens ellipse is analogous) in 3D
in implicit form (see Figure 18.6):
The 2D projections of this elliptical 3D curve in either the ( ,
, ), (
), ( ,
,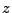 ) or (
) or ( ,
,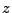 )
plane are themselves ellipses, however the 2D projections of
)
plane are themselves ellipses, however the 2D projections of
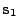 and
and 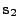 do no longer correspond to the 2D elliptical major and minor semi-axes.
They generally are oblique to each other and their scalar product is non-zero. We will therefore develop
general formulas taking the possible reduction of 3D to 2D into account.
The square of the radial distance for any point on that curve from the global origin is
do no longer correspond to the 2D elliptical major and minor semi-axes.
They generally are oblique to each other and their scalar product is non-zero. We will therefore develop
general formulas taking the possible reduction of 3D to 2D into account.
The square of the radial distance for any point on that curve from the global origin is
Differentiating with respect to 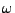 and setting equal to zero leads to the minimax
equation
and setting equal to zero leads to the minimax
equation
where
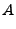 |
 |
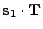 |
(18.133) |
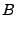 |
 |
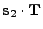 |
(18.134) |
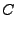 |
 |
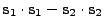 |
(18.135) |
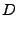 |
 |
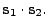 |
(18.136) |
The minimax equation 18.132 contains a mixed trigonometric term and can
only be solved by eliminating either the sine or the cosine function. This leads in general
to a quartic equation
whose coefficients are, depending on if  is either
is either
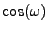 or
or
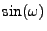 :
All four
:
All four 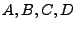 can have a value of zero. The coefficient of
can have a value of zero. The coefficient of 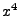 plays a special role.
Note, that for this coefficient to be zero, both
plays a special role.
Note, that for this coefficient to be zero, both 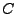 and
and  must be zero, which corresponds
to a circular curve in both 3D and 2D. For a circular target the quartic reduces to a quadratic.
For the 3D cases we always have
must be zero, which corresponds
to a circular curve in both 3D and 2D. For a circular target the quartic reduces to a quadratic.
For the 3D cases we always have  . The following table 18.4
shows the different cases that can arise for 3D, together with a description of the geometrical
shapes of the target figures involved and the corresponding maximum and minimum radial distances:
. The following table 18.4
shows the different cases that can arise for 3D, together with a description of the geometrical
shapes of the target figures involved and the corresponding maximum and minimum radial distances:
Table:
Different cases arising in 3D, depending on values of 
 |
 |
 |
 |
Shape |
 |
 |
| 0 |
0 |
0 |
0 |
Circle (radius
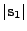 ) ) |
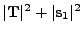 |
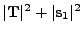 |
| 0 |
0 |
0 |
 |
Tilted circle |
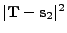 |
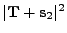 |
| 0 |
0 |
 |
0 |
Tilted circle |
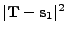 |
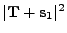 |
| 0 |
0 |
 |
 |
Double-tilted circle |
Solve quadratic |
| 0 |
 |
0 |
0 |
Ellipse |
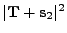 |
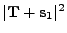 |
| 0 |
 |
0 |
 |
Tilted ellipse |
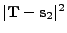 |
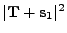 |
| 0 |
 |
 |
0 |
Tilted ellipse |
Solve quadratic product |
| 0 |
 |
 |
 |
Double-tilted ellipse |
Solve quartic |
In this table we have used our convention
 and placement of the
elliptical semi-axes in such a way that the angle they make with
and placement of the
elliptical semi-axes in such a way that the angle they make with 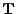 is
is
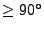 .
The cases that arise for the 2D are summarized in the table 18.5:
.
The cases that arise for the 2D are summarized in the table 18.5:
Table:
Different cases arising in 2D, depending on values of
 |
 |
 |
 |
 |
 |
Shape |
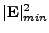 |
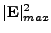 |
| 0 |
0 |
0 |
0 |
0 |
0 |
Point |
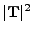 |
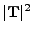 |
| 0 |
 |
0 |
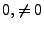 |
0 |
 |
Line (length
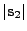 ) ) |
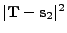 |
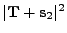 |
| 0 |
 |
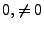 |
0 |
 |
0 |
Line (length
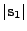 ) ) |
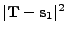 |
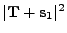 |
| 0 |
0 |
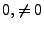 |
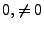 |
 |
 |
Circle (radius
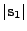 ) ) |
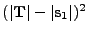 |
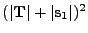 |
| 0 |
 |
0 |
 |
 |
 |
Ellipse (
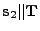 ) ) |
Solve quadratic product |
| 0 |
 |
 |
0 |
 |
 |
Ellipse (
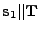 ) ) |
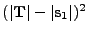 |
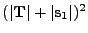 |
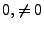 |
 |
 |
 |
 |
 |
Tilted ellipse |
Solve quartic |
When solving the quartic or quadratic product equations, we must remember to eliminate the two non-valid
extra solutions introduced due to squaring. All real solutions between 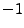 and
and 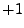 are inserted into
18.131 and the maximum and minimum of all four possible values
are selected.
are inserted into
18.131 and the maximum and minimum of all four possible values
are selected.
18.4.8.4 Initial Placement of the 3D Rays on the 2D Cylindrical Domain
There are two kinds of domain surfaces for a cylindrical domain. The first kind corresponds to
the flat circular surface at both ends of the cylinder. These surfaces are planar and the determination
of the ray intersection position on these surfaces proceeds along the same lines as shown in
section 18.4.7.6. The second kind of surface is the cylinder mantle, whose
geometrical equation is:
Inserting the parametric ray line equation 18.112, we obtain a quadratic equation
in 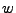 :
:
where only the  and
and  components of the vectors are taken to form the scalar products.
Having found the appropriate
components of the vectors are taken to form the scalar products.
Having found the appropriate 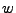 for each ray and the corresponding crossing point
for each ray and the corresponding crossing point
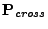 on the domain cylindrical surface, we need to translate the ray 3D domain crossing coordinates
on the domain cylindrical surface, we need to translate the ray 3D domain crossing coordinates
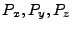 into the initial ray 2D cylindrical wedge coordinates
into the initial ray 2D cylindrical wedge coordinates
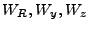 , where
, where 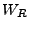 and
and 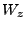 correspond to the 2D cylindrical domain and
correspond to the 2D cylindrical domain and 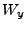 is the linearized angular coordinate from
18.128. Since the starting angular point is irrelevant (there
is no preference of any point on the circle), we set this point equal to zero. Thus:
is the linearized angular coordinate from
18.128. Since the starting angular point is irrelevant (there
is no preference of any point on the circle), we set this point equal to zero. Thus:
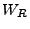 |
 |
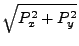 |
(18.140) |
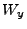 |
 |
0 |
(18.141) |
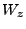 |
 |
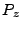 |
(18.142) |
To determine the initial ray wedge velocities, we define two unit vectors of the 3D ray vector:
1) the unit vector in the ( ,
, )-plane and 2) the unit vector along the
)-plane and 2) the unit vector along the 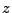 -axis:
-axis:
where
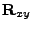 is the (
is the ( ,
, )-plane projection of the 3D ray vector. Likewise, the crossing point
vector is also split into two components:
)-plane projection of the 3D ray vector. Likewise, the crossing point
vector is also split into two components:
Since the origin of the cylindrical domain is located at
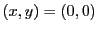 , the vector
, the vector
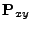 is a radial vector in the (
is a radial vector in the ( ,
, )-plane. The ray vector component
)-plane. The ray vector component
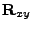 on the other
hand is usually not radially oriented, because the ray's origin (on the lens) does not necessarily
lay on the
on the other
hand is usually not radially oriented, because the ray's origin (on the lens) does not necessarily
lay on the
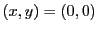 line. Both vectors
line. Both vectors
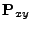 and
and
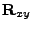 are useful in order
to determine the ray's initial wedge velocities (see Figure 18.10).
are useful in order
to determine the ray's initial wedge velocities (see Figure 18.10).
Figure:
Initial radial (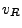 ) and angular (
) and angular (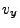 ) ray velocity
components on the wedge from vectors
) ray velocity
components on the wedge from vectors
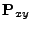 and
and
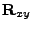 .
.
|
|
Denote the angle between
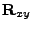 and
and
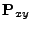 by
by 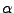 . Then
. Then
and the initial ray wedge velocities are
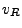 |
 |
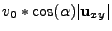 |
(18.147) |
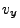 |
 |
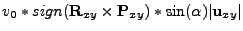 |
(18.148) |
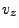 |
 |
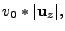 |
(18.149) |
where the sine and the cross product vector present in the expression for
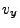 are calculated as
are calculated as
and
The sign of the cross product refers to the sign of the 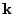 component. Note, that
the wedge's
component. Note, that
the wedge's  -direction refers to the cylindrical
-direction refers to the cylindrical 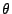 -coordinate and the convention
is that counterclockwise rotation along
-coordinate and the convention
is that counterclockwise rotation along 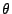 is considered positive.
is considered positive.
18.4.8.5 Tracing the Rays through the Truncated Wedges
Figure 18.11:
Change in position and velocity components when
ray moves into a new wedge. For clarity, the velocity components in the original wedge are
shifted from the boundary crossing point.
|
|
When a ray hits the 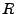 - or
- or 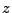 -planes of a truncated wedge, the
-planes of a truncated wedge, the 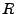 - or
- or 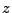 -components of
the ray's position and velocity change the same way as for a pure 2D cylindrical simulation.
The
-components of
the ray's position and velocity change the same way as for a pure 2D cylindrical simulation.
The  -components stay the same. When the ray hits the
-components stay the same. When the ray hits the  -planes of the truncated wedge,
it will cross into a new rotated wedge and the
-planes of the truncated wedge,
it will cross into a new rotated wedge and the  -position and the
-position and the 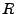 - and
- and  -components
of the velocity must change to reflect that rotation. The change in
-components
of the velocity must change to reflect that rotation. The change in  -position is simple:
just invert its sign. For the velocity component changes we need the cosine and sine of the
wedge's opening angle
-position is simple:
just invert its sign. For the velocity component changes we need the cosine and sine of the
wedge's opening angle 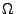 . The new components are thus
. The new components are thus
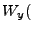 new new |
 |
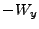 |
(18.152) |
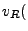 new new |
 |
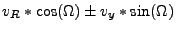 |
(18.153) |
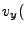 new new |
 |
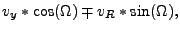 |
(18.154) |
where the sign options in 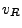 and
and 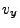 correspond to the two possible
correspond to the two possible  -planes defined
in 18.128 (see Figure 18.11).
The change in direction of both velocity vector components is not a rotational effect
on the ray due to the medium through which it travels but rather a geometrical effect due
to changing wedges. When crossing a common
-planes defined
in 18.128 (see Figure 18.11).
The change in direction of both velocity vector components is not a rotational effect
on the ray due to the medium through which it travels but rather a geometrical effect due
to changing wedges. When crossing a common  -plane between two wedges, the ray is still on
the same position in the (
-plane between two wedges, the ray is still on
the same position in the (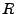 ,
,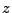 ) 2D cylindrical plane. Note, that
) 2D cylindrical plane. Note, that 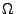 must not necessarily
be a divisor of
must not necessarily
be a divisor of  . Since
. Since 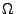 is fixed through the entire simulation,
is fixed through the entire simulation,
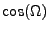 and
and
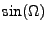 are conveniently computed only once during initialization.
are conveniently computed only once during initialization.
18.4.9 Ray Tracing in 3D Cylindrical Domains
Ray tracing in 3D cylindrical domains starts from the acceleration vector definition at
a point 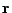 in 3D cylindrical coordinates
in 3D cylindrical coordinates
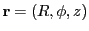 in terms of their
rotating unit vectors
in terms of their
rotating unit vectors
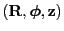 , the ray equation of motion
in Eq.(18.36) and the definition of the gradient operator in 3D
cylindrical coordinates:
, the ray equation of motion
in Eq.(18.36) and the definition of the gradient operator in 3D
cylindrical coordinates:
the ray equation of motion Eq.(18.36):
and the definition of the gradient operator in 3D cylindrical coordinates:
The 3D cylindrical ray equation of motion equations become:
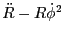 |
 |
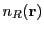 |
(18.158) |
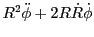 |
 |
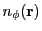 |
(18.159) |
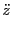 |
 |
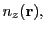 |
(18.160) |
where
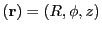 and:
and:
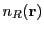 |
 |
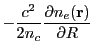 |
(18.161) |
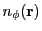 |
 |
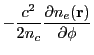 |
(18.162) |
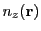 |
 |
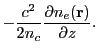 |
(18.163) |
Since  is given in dimensionless radian units, the units of the partial
3D cylindrical gradients of the electron number density are:
is given in dimensionless radian units, the units of the partial
3D cylindrical gradients of the electron number density are:  in cm/s
in cm/s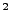 ,
,
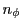 in cm
in cm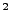 /s
/s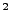 and
and 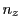 in cm/s
in cm/s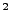 . The radial acceleration and
velocity is
. The radial acceleration and
velocity is 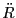 and
and 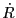 in cm/s
in cm/s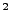 and cm/s, the angular acceleration
and velocity is
and cm/s, the angular acceleration
and velocity is
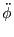 and
and 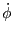 in rad/s
in rad/s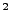 and rad/s.
and rad/s.
As the use of angular acceleration 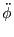 and velocity
and velocity 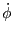 is
computationally somewhat inconvenient, we will transform these to the tangential
acceleration
is
computationally somewhat inconvenient, we will transform these to the tangential
acceleration
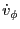 and velocity
and velocity 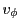 by using:
by using:
Using the tangential variables, Eqs.(18.158-18.160)
can be cast into the six 1st order ODEs:
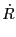 |
 |
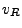 |
(18.166) |
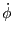 |
 |
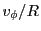 |
(18.167) |
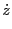 |
 |
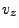 |
(18.168) |
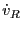 |
 |
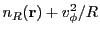 |
(18.169) |
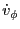 |
 |
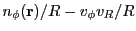 |
(18.170) |
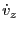 |
 |
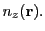 |
(18.171) |
Even for constant electron number density gradients, there are no analytical solutions
for 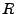 and
and 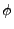 in time, and hence one must resort to numerical methods like
Runge-Kutta (RK). Starting from initial values
in time, and hence one must resort to numerical methods like
Runge-Kutta (RK). Starting from initial values
 inside a 3D cylindrical
cell or on one of its walls, a RK time step is performed such that: 1) we stay inside
the cell or hit one of its walls, 2) the RK step is within accuracy bounds and
3) is computationally stable. We would like to have a RK method which allows one
to directly calculate the time it would take for one RK step to hit exactly the cell walls.
This would avoid an iterative approach to the cell walls, which is computationally very time
consuming. The second order RK2 methods are ideally suited for that purpose. A generic RK2
time step
inside a 3D cylindrical
cell or on one of its walls, a RK time step is performed such that: 1) we stay inside
the cell or hit one of its walls, 2) the RK step is within accuracy bounds and
3) is computationally stable. We would like to have a RK method which allows one
to directly calculate the time it would take for one RK step to hit exactly the cell walls.
This would avoid an iterative approach to the cell walls, which is computationally very time
consuming. The second order RK2 methods are ideally suited for that purpose. A generic RK2
time step 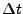 on the above set of six 3D cylindrical ODE's gives new updated
values (left updated variables, right old variables):
on the above set of six 3D cylindrical ODE's gives new updated
values (left updated variables, right old variables):
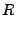 |
 |
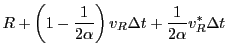 |
(18.172) |
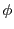 |
 |
![$\displaystyle \phi + \left(1-\frac{1}{2\alpha}\right)\left[\frac{v_\phi}{R}\right]{\Delta t}
+ \frac{1}{2\alpha}\left[\frac{v_\phi^{*}}{R^{*}}\right]{\Delta t}$](img1615.png) |
(18.173) |
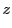 |
 |
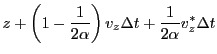 |
(18.174) |
and new velocity values:
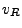 |
 |
![$\displaystyle v_R
+ \left(1-\frac{1}{2\alpha}\right)
\left[n_R({\bf r}) + \frac...
...2\alpha}
\left[n_R({\bf r}^{*}) + \frac{{v_\phi^{*}}^2}{R^{*}}\right]{\Delta t}$](img1618.png) |
(18.175) |
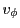 |
 |
![$\displaystyle v_\phi
+ \left(1-\frac{1}{2\alpha}\right)
\left[\frac{n_\phi({\bf...
...{n_\phi({\bf r}^{*})}{R^{*}} - \frac{v_\phi^{*}v_R^{*}}{R^{*}}\right]{\Delta t}$](img1619.png) |
(18.176) |
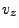 |
 |
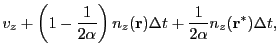 |
(18.177) |
where
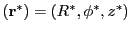 and:
and:
 |
 |
 |
(18.178) |
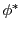 |
 |
![$\displaystyle \phi + \alpha\left[v_\phi/R\right]{\Delta t}$](img1625.png) |
(18.179) |
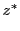 |
 |
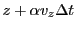 |
(18.180) |
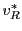 |
 |
![$\displaystyle v_R + \alpha\left[n_R({\bf r}) + v_\phi^2/R\right]{\Delta t}$](img1629.png) |
(18.181) |
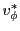 |
 |
![$\displaystyle v_\phi + \alpha\left[n_\phi({\bf r})/R - v_\phi v_R/R\right]{\Delta t}$](img1631.png) |
(18.182) |
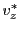 |
 |
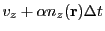 |
(18.183) |
are the intermediate state values. 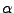 is a numerical parameter and although it can in principle
be set to any value for the generic RK2 scheme to be second order, by far the most common choice is to
set
is a numerical parameter and although it can in principle
be set to any value for the generic RK2 scheme to be second order, by far the most common choice is to
set 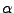 in the range
in the range ![$[1/2,1]$](img1634.png) . Due to the second order nature of the generic RK2 schemes,
it allows us to find the
. Due to the second order nature of the generic RK2 schemes,
it allows us to find the 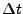 values to hit the cell walls by solving simple quadratic
equations. Using Eqs.(18.172-18.174) and the intermediate
values in Eqs.(18.178-18.183), we have
values to hit the cell walls by solving simple quadratic
equations. Using Eqs.(18.172-18.174) and the intermediate
values in Eqs.(18.178-18.183), we have 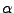 independent
radial and axial cell wall polynomials in
independent
radial and axial cell wall polynomials in 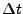 and an
and an 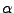 dependent
angular cell wall polynomial:
dependent
angular cell wall polynomial:
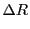 |
 |
![$\displaystyle v_R{\Delta t} + \frac{1}{2}\left[n_R({\bf r}) + \frac{v_\phi^2}{R}\right]{\Delta t}^2$](img1636.png) |
(18.184) |
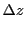 |
 |
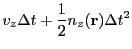 |
(18.185) |
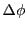 |
 |
![$\displaystyle \left[\frac{v_\phi}{R} - \alpha\frac{v_R\Delta\phi}{R}\right]{\De...
...right)\frac{v_\phi v_R}{R^2} + \frac{n_\phi({\bf r})}{2R^2}\right]{\Delta t}^2,$](img1640.png) |
(18.186) |
where
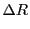 |
 |
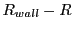 |
(18.187) |
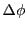 |
 |
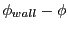 |
(18.188) |
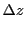 |
 |
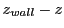 |
(18.189) |
Note that these quadratic equations do not involve electron number density gradients at the intermediate
points, like for example
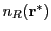 . Higher order RK methods will introduce these density gradients
in expressions for
. Higher order RK methods will introduce these density gradients
in expressions for 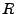 ,
, 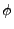 and
and 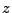 thus leading to much more complex equations in
thus leading to much more complex equations in 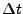 .
Also cell sizes, especially for highly refined domains, are usually small, hence a higher order RK method,
besides having the problem of complicated radial, angular and axial
.
Also cell sizes, especially for highly refined domains, are usually small, hence a higher order RK method,
besides having the problem of complicated radial, angular and axial 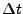 expansions, would involve
lots of computational work for a modest gain in number of RK steps inside the cell. Typically one would
need only up to three RK2 steps vs maybe one RK4 step inside a cell. The effort of a higher order RK method
simply does not pay off.
expansions, would involve
lots of computational work for a modest gain in number of RK steps inside the cell. Typically one would
need only up to three RK2 steps vs maybe one RK4 step inside a cell. The effort of a higher order RK method
simply does not pay off.
Let us denote the minimum
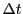 (excluding zero) obtained from solving all six (two for each
kind of cell wall) polynomials in Eqs.(18.184-18.186) as
(excluding zero) obtained from solving all six (two for each
kind of cell wall) polynomials in Eqs.(18.184-18.186) as
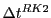 . Using
. Using
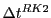 to obtain new positions via
Eqs.(18.172-18.174) guarantees that we stay inside the cell, but using it
to determine the intermediate state via Eqs.(18.178-18.180) might
take us outside of the cell, i.e.
to obtain new positions via
Eqs.(18.172-18.174) guarantees that we stay inside the cell, but using it
to determine the intermediate state via Eqs.(18.178-18.180) might
take us outside of the cell, i.e.
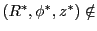 cell. To enforce the
intermediate state inside the cell, we determine also the minimum
cell. To enforce the
intermediate state inside the cell, we determine also the minimum
 (excluding zero)
obtained from solving all six (two for each kind of cell wall) linear intermediate state equations
in Eqs.(18.178-18.180) by replacing
(excluding zero)
obtained from solving all six (two for each kind of cell wall) linear intermediate state equations
in Eqs.(18.178-18.180) by replacing
 by the
corresponding cell wall values. Denoting this minimum intermediate state
linear time as
by the
corresponding cell wall values. Denoting this minimum intermediate state
linear time as
 , we form the allowed stepping time
, we form the allowed stepping time
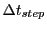 inside the
cell as:
inside the
cell as:
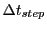 might take the ray to a cell wall (
might take the ray to a cell wall (
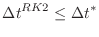 ) or
to a position still inside the cell (
) or
to a position still inside the cell (
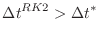 ). The last case happens,
when the intermediate state lays outside the cell and is an indication that the ray wants to turn
into opposite direction for a particular coordinate (opposite velocity and acceleration
direction), as shown in Figure 18.12.
). The last case happens,
when the intermediate state lays outside the cell and is an indication that the ray wants to turn
into opposite direction for a particular coordinate (opposite velocity and acceleration
direction), as shown in Figure 18.12.
Figure 18.12:
Showing a ray turning inside a 3D cylindrical cell
due to opposite radial velocity and acceleration direction.
|
|
Each bullet represents a different stepping time inside the cell. From
Eqs.(18.178-18.180) we see, that generally
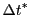 will be largest the smaller
will be largest the smaller 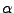 is, hence we choose
is, hence we choose
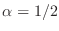 (midpoint RK2 method).
The following 3D cylindrical ray tracing algorithm has been implemented:
(midpoint RK2 method).
The following 3D cylindrical ray tracing algorithm has been implemented:
- From a position in or on a cell wall, determine minimum parabolic RK2 time
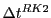 (excluding zero time) to one of the cell walls.
(excluding zero time) to one of the cell walls.
- From same position, determine minimum linear intermediate state time
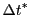 (excluding
zero time) to one of the cell walls.
(excluding
zero time) to one of the cell walls.
- Do a RK2 step (Eqs.(18.172-18.177)) with stepping time
 followed by 2 RK2 steps
with half stepping time
followed by 2 RK2 steps
with half stepping time
 .
.
- Calculate and analyze errors in position and velocity. If any of the errors is too large, estimate
safe stepping time
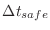 and redo the RK2 step. Since
and redo the RK2 step. Since
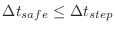 , we still stay inside the cell.
, we still stay inside the cell.
- If not yet on a cell wall, repeat.
Currently the 3D cylindrical ray tracing has only been implemented for the cell average AVG
algorithm (section 18.4.4.1), in which the radial, angular and axial electron
number gradients in Eqs.(18.161-18.163) are constant for each cell.
Only convex 3D cylindrical domains are treatable in which the angular domain coordinates extend
over the full circle. Concave 3D cylindrical domains with partial angular domain coordinates
are not planned for the near future. Error bounds in position are defined as a predefined
fraction (tolerance) of cell dimensions along each coordinate. Error bounds in velocity are defined
as a predefined fraction of the ray speed in the cell before applying the RK2 step. Rather than using
the speed
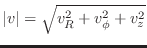 itself, we use the sum of the absolute components
itself, we use the sum of the absolute components
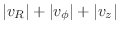 , as this is computationally much more economical to evaluate and is in
error compared to the speed by a factor of
, as this is computationally much more economical to evaluate and is in
error compared to the speed by a factor of 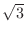 at most.
at most.
Rays crossing the 3D cylindrical axis at  need a special treatment, as 3D cylindrical blocks
touching the axis have no meaningful neighbor block information. To outline the strategy, we
consider the 3D cylindrical axis to be hollow and to have a finite tiny radius
need a special treatment, as 3D cylindrical blocks
touching the axis have no meaningful neighbor block information. To outline the strategy, we
consider the 3D cylindrical axis to be hollow and to have a finite tiny radius  with no radial, angular
and axial acceleration terms (
with no radial, angular
and axial acceleration terms (
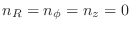 ). Figure 18.13
shows a ray crossing the hollow axis.
). Figure 18.13
shows a ray crossing the hollow axis.
Figure 18.13:
Showing a ray passing through a hollow 3D cylindrical axis.
|
|
If no acceleration terms are present, the 3D cylindrical ray equation of motion ODEs in
Eqs.(18.166-18.171) have an exact analytical solution:
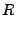 |
 |
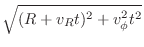 |
(18.191) |
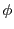 |
 |
![$\displaystyle \phi + \arctan{\left[v_\phi t/(R + v_Rt)\right]}$](img1666.png) |
(18.192) |
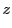 |
 |
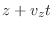 |
(18.193) |
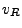 |
 |
![$\displaystyle \left[(v_R^2 + v_\phi^2)t + R\right] / \sqrt{(R + v_Rt)^2+v_\phi^2t^2}$](img1668.png) |
(18.194) |
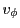 |
 |
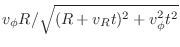 |
(18.195) |
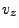 |
 |
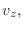 |
(18.196) |
which represents movement along a straight line in 3D cylindrical coordinates. When a ray
enters the hollow axis at 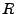 , it must also exit the axis at
, it must also exit the axis at 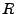 , hence the time it
takes to cross the hollow axis is the solution in
, hence the time it
takes to cross the hollow axis is the solution in 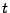 of Eq.(18.191):
of Eq.(18.191):
which, when inserted in Eqs.(18.191-18.196) gives:
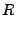 |
 |
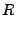 |
(18.198) |
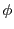 |
 |
![$\displaystyle \phi + \arctan{\left[2v_Rv_\phi/(v_R^2 - v_\phi^2)\right]}$](img1673.png) |
(18.199) |
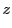 |
 |
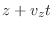 |
(18.200) |
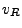 |
 |
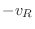 |
(18.201) |
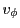 |
 |
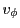 |
(18.202) |
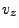 |
 |
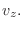 |
(18.203) |
Taking the limit
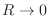 in which the hollow axis becomes a line, we have
in which the hollow axis becomes a line, we have 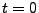 and
and
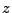 ,
, 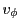 ,
, 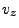 retain their values while the radial velocity changes sign. The new angle
after crossing the axis is only dependent on the initial angle and the radial and tangential
angular velocity and given by Eq.(18.199).
Figure 18.14 shows various cases of new ray angle values
depending on initial radial and tangential angular velocities.
retain their values while the radial velocity changes sign. The new angle
after crossing the axis is only dependent on the initial angle and the radial and tangential
angular velocity and given by Eq.(18.199).
Figure 18.14 shows various cases of new ray angle values
depending on initial radial and tangential angular velocities.
Figure 18.14:
Various examples of new ray angle values
depending on initial radial and tangential angular velocities.
|
|
Direct application of Eq.(18.199) is, however, not recommended,
due to the possibility of zero or near zero of the denominator
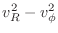 , leading
to computational overflow. We can transform the arctan expression into two equivalent forms
by dividing both nominator and denominator by
, leading
to computational overflow. We can transform the arctan expression into two equivalent forms
by dividing both nominator and denominator by 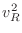 or
or 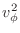 and using the arctan
addition formula, giving:
and using the arctan
addition formula, giving:
We apply the first equation whenever
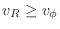 and the second otherwise, thus ensuring
an arctan value
and the second otherwise, thus ensuring
an arctan value  for all cases.
for all cases.
18.4.10 Synchronous and Asynchronous Ray Tracing
The default laser implementation uses the Lagrangian particle
framework to move rays (modeled as particles) across block and process
boundaries. We generally find that particle movement consumes a
relatively small portion of total runtime even in large-scale
simulations with millions of particles (Dubey et al., 2012). This is
not always case in laser-driven FLASH simulations, where realistic
simulations can spend the majority of runtime moving rays between
blocks. The reason for the discrepancy in performance is because a ray
generally travels a much larger distance than a tracer particle in a
single time-step. In the tracer particle case we only need one
application of the communication subroutines in a single time-step
because a particle never moves further than a nearest-neighbor block
(see CFL limit). In contrast a ray can move to the other side of the
domain in a single time-step which may involve visiting hundreds of
intermediate blocks.
There are various implementations of particle exchange in the
GridParticles sub-unit. In order to understand the performance
bottlenecks, we describe the default implementation used in FLASH
applications configured with Paramesh. The particle movement
communication consists of an MPI_Allreduce to determine the
number of particles and messages that each MPI rank will receive,
followed by point to point messages which exchange the actual
particles. In addition to the communication in the GridParticles unit,
there is also an MPI_Allreduce in the laser unit which
determines if all the rays have either left the domain or have been
absorbed. This is the termination criteria and controls whether
another round of particle exchange is needed.
Performance profiles of simulations using the laser indicate that most
time is spent in MPI_Allreduce calls in a particle movement
subroutine. The trace in Figure 18.15 shows that
this happens because of load imbalance and not slowness of the
underlying collective communication call. The two main colors in this
trace are red and purple; red is time spent in a computational kernel
named ed_traceBlockRays2Dcyl3D and purple is time spent in
MPI_Allreduce. We see that the color map is dominated by
purple which indicates most MPI ranks are waiting for the
MPI_Allreduce to complete. The cascading red pattern shows
the ray paths as rays move between blocks assigned to different MPI
ranks. It is clear that there are many round of bulk synchronous
particle exchange and that some MPI ranks must wait a long time before
receiving any rays.
Figure 18.15:
Performance trace of MPI ranks 0-33 in a laser simulation
using synchronous communication and run with 2048 MPI ranks on Intrepid BG/P.
|
|
The biggest impediment to good performance is the dependency between
MPI ranks which happens because ray paths are not known ahead of
time. Performance quickly degrades at higher processor counts because
increased domain decomposition means rays must cross more process
boundaries. One approach to improve performance would be to use the
mesh replication feature of FLASH to trivially parallelize over the
rays, but this is not ideal because it introduces redundant
computations of e.g. hydrodynamics in each mesh. The approach we take
is to introduce pipelined parallelism to hide the dependency between
MPI ranks; rays are sent to nearest-neighbor blocks on different MPI
ranks as early as possible to minimize the time MPI ranks must wait
for work. Computation and communication are overlapped, which is
different to the current bulk synchronous approach where there are
distinct computation and communication phases. The “asynchronous ray
trace” is included in a FLASH application by setting up with the
shortcut +asyncLaser. We describe the ray exchange and
termination communication kernels in the asynchronous scheme below.
The ray exchange communication kernel requires all MPI ranks set up
designated send and receive communication channels with only those MPI
ranks which own nearest-neighbor blocks. This is a relatively small
subset because of the block locality in Paramesh. We post one
speculative non-blocking receive for each neighbor and then test all
communication channels (at a rate determined by runtime parameter
ed_commRaysBetweenMsgTest) for new rays. When an MPI rank
receives a message we copy the rays and then post a new speculative
non-blocking receive. This ensures that a message can be received from
any nearest neighbor at any time. We send rays using non-blocking
sends from source MPI ranks when send buffers (of size determined by
runtime parameter ed_commChannelSize) are full. At idle
phases, we also send rays before the send buffer is full to prevent
deadlock and ensure good global progress. When exchange is complete
all MPI ranks send a zero byte message to each neighboring MPI rank to
match the remaining speculative receives.
The termination communication kernel must also be non-blocking to
allow progress in the ray exchange communication kernel. This rules
out using a blocking MPI_Allreduce as is used in the default
synchronous scheme. We have multiple non-blocking implementations of
the termination kernel which all have different library and MPI
dependencies. The default implementation, which has no special
dependencies, uses a master-slave approach to determine completion. It
works by sending a count of local inactive rays from slaves to a
master which maintains a count of global inactive rays. We send a
notification message from the master to the slaves when the global
number of inactive rays is equal to the initial count of active
rays. Even though we have demonstrated that this implementation
can work when using 8192 MPI ranks on Intrepid BG/P, there is a
danger of exceeding internal MPI limits on the number of messages the
master rank can receive. For this reason we have created another
implementation which uses a non-blocking MPI_Iallreduce
which is part of MPI-3. We recommend using this implementation because
there is less danger of exceeding internal MPI limits. It can be used
by setting up a FLASH application with the setup shortcut
+mpi3. Given that the MPI-3 standard is still quite new, it
is likely that some MPI implementations on today's production machines
do not support non-blocking collectives. Therefore, we also support
the non-blocking reduction in the Non Blocking Collectives (NBC)
library http://htor.inf.ethz.ch/research/nbcoll/libnbc/. The
necessary reduction name substitutions happen when a FLASH application
is setup with +libnbc.
We repeat the experiment in Figure 18.15 with the
asynchronous communication scheme and show results in Figure
18.16. The number of ranks on the y-axis and
time scale on the x-axis are the same as before. The color map is much
more chaotic than before because all MPI ranks are either computing or
spinning in various subroutines looking for more work. As before, the
red color indicates time spent in a computational kernel named
ed_traceBlockRays2Dcyl3D. The red is now much more clustered
on the left side of the figure indicating MPI ranks wait less time for
rays than before. We see large segments of green for MPI rank 0 which
indicates time spent testing for new messages. This is happening
because we made use of the master-slave termination kernel in this
test. A performance comparison of the synchronous and asynchronous
communication schemes is shown in Figure 18.17.
Figure 18.16:
Performance trace of MPI ranks 0-33 in a laser
simulation using asynchronous communication and run with 2048 MPI ranks on Intrepid BG/P.
|
|
Figure 18.17:
Strong scaling of a laser simulation run on
Intrepid BG/P with the synchronous and asynchronous communication scheme.
|
|
The parameters ed_commChannelSize and
ed_commRaysBetweenMsgTest give some control over the memory
overhead and performance of the asynchronous scheme. The
ed_commChannelSize parameter should be kept relatively small
because it determines the amount of space available for rays in send
and receive buffers. Large values lead to a very high memory footprint
because there is a designated portion of space in the buffers for all
communication channels (i.e. all possible pairs of communicating
processors) and there can be 10-100s of communication channels. The
parameter also determines the number of rays which are buffered before
being sent from source processors to destination processors, and so
smaller values will improve overall load balance. All messages are
non-blocking and so the source processor returns immediately to
computation and is free to send rays to different destination
processors. However, the source processor will block (actually spin on
various MPI_Test statements with no danger of deadlock) if a
ray should be sent to the original processor and the original message
is not yet delivered. This means it is important for the destination
processor to frequently check for new messages not only to start work
as soon as possible but also to enable the source processor to return
to useful work. The parameter ed_commRaysBetweenMsgTest
should therefore be kept relatively small so that the destination
processor performs less computational work between message checks.
We set the default values of ed_commRaysBetweenMsgTest=50
and ed_commChannelSize=100. Very small values for both
parameters improve load balance but introduce new overheads such as
the cost of continually testing for new messages and the cost of
preparing the laser computation routines for the newly received
rays. The preparation work includes sorting the rays in block order
and then scanning the ray array to find the start and end index for
each block. Sorting improves the memory-access pattern and is a
sensible optimization when computational time is large relative to the
sort time (as always happens in the original synchronous communication
scheme), however, it hurts performance when computational work is very
fine-grained. Hence, we do not advise using parameter values much
smaller than the default values. In future it would be interesting to
see if removing the serial optimization improves the global time to
solution. This could happen because more processors are doing useful
work despite there being worse memory-access on each processor.
The asynchronous communication scheme conflicts with various
capabilities in FLASH. It only works with Paramesh at the current
time, although support for UG could probably be added without a huge
amount of effort. We initially did not support UG because we did not
know the MPI rank IDs of the corner neighboring blocks, although this
is no longer the case. It also conflicts with the Laser I/O.
The asynchronous communication scheme is able to run without the
GridParticles dependency by setting up with
useGridParticles=False. This is generally a good idea because
the GridParticles sub-unit has initialization code which allocates
large send and receive buffers for bulk synchronous
communication. These buffers are not needed in the asynchronous scheme
and so removing the dependency significantly reduces the memory
footprint. The only down-side is that a slower sorting subroutine will
be used in place of Grid_SortParticles, which is able to achieve a
fast sort by using the space in the bulk synchronous communication
buffers.
The new asynchronous ray tracing implementation works and has been tested with several laser
problems using multiple compilers and MPI implementations. However, since this is a rather new
implementation, the asynchronous ray tracing mode should still be considered as being in its
experimental stage. Both synschronous and asynchronous ray tracing modes are currently made
available, with synchronous mode being the default. The asynchronous mode can be activated
by using the appropriate setup parameter.
18.4.11 Usage
To include the use of the Energy Deposition unit, the following should be included into the
setup line command:
+laser ed_maxPulses=<number> ed_maxPulseSections=<number> ed_maxBeams=<number>
- ed_maxPulses: The maximum number of different laser pulses for the simulation.
- ed_maxPulseSections: The maximum number of power/time pairs per pulse.
- ed_maxBeams: The maximum number laser beams for the simulation.
The Energy Deposition unit reads all the information it needs to construct the laser beams and
pulses from runtime parameters specified in the flash.par file. Below is the list of runtime
parameters that is needed to properly build the laser. For clarification and figuring out
the input to a particular laser simulation, the reader is encouraged to have Figures
18.5, 18.6 and 18.7 at hand.
- ed_numberOfSections_n: Indicates
the number of power/time pairs that are going to be used to set up the shape of the n-th laser pulse.
There must be at least as many of these runtime parameters as there are number of laser pulses defined,
i.e. n = 1,...,ed_numberOfPulses.
- ed_power_n_i: Sets the i-th power
of the i-th power/time pair of the n-th laser pulse. The ranges of the indices must be at
least: i = 1,...,ed_numberOfSections_n and
n = 1,...,ed_numberOfPulses.
- ed_time_n_i: Sets the i-th time
of the i-th power/time pair of the n-th laser pulse. The ranges
of the indices must be at least: i = 1,...,ed_numberOfSections_n
and n = 1,...,ed_numberOfPulses.
- ed_adjustInitialRaySpeed: If true, the initial ray speed of the speed
of light will be adjusted (lowered) by a factor of
 when the ray enters
the domain depending on the electron number density
when the ray enters
the domain depending on the electron number density 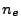 encountered in the first entry cell
(n-th beam).
encountered in the first entry cell
(n-th beam).
- ed_crossSectionFunctionType_n: Beam cross section power function (flat or
gaussian decay) type. For a flat profile use 'uniform', for gaussian decay use 'gaussian1D'
(two-dimensional beams) or 'gaussian2D' (three-dimensional beams) (n-th beam).
- ed_gaussianCenterMajor_n: The Gaussian center location along the
major elliptical semiaxis (n-th beam).
- ed_gaussianCenterMinor_n: The Gaussian center location along the
minor elliptical semiaxis (n-th beam).
- ed_gaussianExponent_n: The Gaussian super exponent
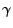 for the beam
cross section power function in equation 18.106 (n-th beam).
for the beam
cross section power function in equation 18.106 (n-th beam).
- ed_gaussianRadiusMajor_n: The Gaussian radius (e-folding length)
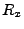 along the
major elliptical semiaxis in equation18.106 (n-th beam).
along the
major elliptical semiaxis in equation18.106 (n-th beam).
- ed_gaussianRadiusMinor_n: The Gaussian radius (e-folding length)
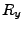 along the
minor elliptical semiaxis in equation18.106 (n-th beam).
along the
minor elliptical semiaxis in equation18.106 (n-th beam).
- ed_gridDeltaSemiAxisMajor_n: For delta grid types, the tic separation along
the major elliptical semiaxis (n-th beam).
- ed_gridDeltaSemiAxisMinor_n: For delta grid types, the tic separation along
the minor elliptical semiaxis (n-th beam).
- ed_gridnAngularTics_n: For radial grid types, the number of wanted angular
slices (n-th beam).
- ed_gridnRadialTics_n: For radial grid types, the number of wanted grid
positions along each radial spike (n-th beam).
- ed_gridnSemiAxisMajorTics_n: For rectangular grid types, the number of wanted
grid positions along the major semi axis (n-th beam).
- ed_gridnSemiAxisMinorTics_n: For rectangular grid types, the number of wanted
grid positions along the minor semi axis (n-th beam).
- ed_gridType_n: Specifies the grid type to be used for placing the rays inside
the beam. For two-dimensional beams the options are 'regular1D' or 'statistical1D'.
For three-dimensional beams the options are 'square2D', 'radial2D' or 'statistical2D'. (n-th beam).
- ed_ignoreBoundaryCondition_n: Ignore the domain boundary conditions (reflective) when
rays enter the domain (n-th beam)?
- ed_lensSemiAxisMajor_n: The major (largest) semiaxis length
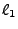 for the
elliptical lens area (n-th beam).
for the
elliptical lens area (n-th beam).
- ed_lensX_n: The x-component of the global lens center position vector
 (n-th beam).
(n-th beam).
- ed_lensY_n: The y-component of the global lens center position
vector
 (n-th beam).
(n-th beam).
- ed_lensZ_n: The z-component of the global lens center position
vector
 (n-th beam).
(n-th beam).
- ed_numberOfRays_n: Number of rays to be created for the beam. Might be
overwritten in 3D geometrical cases (n-th beam).
- ed_pulseNumber_n: The pulse shape identification number (n-th beam).
- ed_semiAxisMajorTorsionAngle_n: The major elliptical semiaxis torsion angle
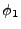 along the beam's lens target center line (n-th beam).
along the beam's lens target center line (n-th beam).
- ed_semiAxisMajorTorsionAxis_n: The major elliptical semiaxis torsion axis
('x','y' or 'z') from which the torsion angle
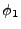 is defined (n-th beam).
is defined (n-th beam).
- ed_targetSemiAxisMajor_n: The major (largest) semiaxis length
 for the
elliptical target area (n-th beam).
for the
elliptical target area (n-th beam).
- ed_targetSemiAxisMinor_n: The minor (smallest) semiaxis length
 for the
elliptical target area (n-th beam).
for the
elliptical target area (n-th beam).
- ed_targetX_n: The x-component of the global target center position
vector
 (n-th beam).
(n-th beam).
- ed_targetY_n: The y-component of the global target center position
vector
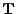 (n-th beam).
(n-th beam).
- ed_targetZ_n: The z-component of the global target center position
vector
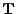 (n-th beam).
(n-th beam).
- ed_wavelength_n: The wavelength of the laser (n-th beam).
- ed_adjustBeamsTargetIntensity: If true, 1D cartesian and 2D cartesian beams
target intensities (power/area) will be adjusted to mimic a cylindrical 3D beam with radius equal to
ed_targetSemiAxisMajor.
- ed_adjustBySymmetryX: If true and ed_createRaysExpandX is also true and
one of the x boundary is reflecting and another x boundary is not reflecting, multiply ray power and ray count by half
to account for double counting in x direction.
- ed_adjustBySymmetryY: If true and ed_createRaysExpandY is also true and
one of the y boundary is reflecting and another y boundary is not reflecting, multiply ray power and ray count by half
to account for double counting in y direction.
- ed_adjustBySymmetryZ: If true and ed_createRaysExpandZ is also true and
one of the z boundary is reflecting and another z boundary is not reflecting, multiply ray power and ray count by half
to account for double counting in z direction.
- ed_beamsCheckExpandX: If true, check beams in both computational domain and expanded (by
reflection or translation in x direction) domain.
- ed_beamsCheckExpandY: If true, check beams in both computational domain and expanded (by
reflection or translation in y direction) domain.
- ed_beamsCheckExpandZ: If true, check beams in both computational domain and expanded (by
reflection or translation in z direction) domain.
- ed_cellStepTolerance: This factor times the smallest dimension of each
cell is taken as the positional error tolerance for step-sized based ray tracing methods.
- ed_cellTimeEnergyDeposition: If set true, the energy deposition by the
laser rays is calculated based only on the time spent in each cell by calculating cell
center values of
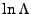 and
and 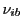 using Eq.(18.46) and replacing the
time integration term in Eq.(18.47) by
using Eq.(18.46) and replacing the
time integration term in Eq.(18.47) by 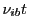 , i.e. treating
, i.e. treating 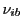 as constant
in the cell. If false, the more expensive time integration formalism from Eq.(18.59)
is used.
as constant
in the cell. If false, the more expensive time integration formalism from Eq.(18.59)
is used.
- ed_cellWallThicknessFactor: Controls the (imaginary) thickness of the cell
walls to ensure computational stability of the laser code. The cell thickness is defined as this
factor times the smallest cell dimension along all geometrical axes. The factor is currently
set to
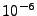 and should only very rarely be changed.
and should only very rarely be changed.
- ed_computeGradNeleR: (AVG algorithm 18.4.4.1 only) If false,
the radial components of the gradients
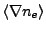 are not computed, i.e. set to zero.
are not computed, i.e. set to zero.
- ed_computeGradNeleP: (AVG algorithm 18.4.4.1 only) If false,
the azimuthal (phi) components of the gradients
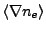 are not computed,
i.e. set to zero.
are not computed,
i.e. set to zero.
- ed_computeGradNeleT: (AVG algorithm 18.4.4.1 only) If false,
the polar (theta) components of the gradients
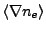 are not computed,
i.e. set to zero.
are not computed,
i.e. set to zero.
- ed_computeGradNeleX: (AVG algorithm 18.4.4.1 only) If false,
the x-components of the gradients
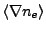 are not computed, i.e. set to zero.
are not computed, i.e. set to zero.
- ed_computeGradNeleY: (AVG algorithm 18.4.4.1 only) If false,
the y-components of the gradients
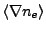 are not computed, i.e. set to zero.
are not computed, i.e. set to zero.
- ed_computeGradNeleZ: (AVG algorithm 18.4.4.1 only) If false,
the z-components of the gradients
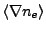 are not computed, i.e. set to zero.
are not computed, i.e. set to zero.
- ed_createRaysExpandX: If true, create rays in both computational domain and expanded (by
reflection or translation in x direction) domain. If the created ray is in the expanded portion, then map the ray to the
computational domain.
- ed_createRaysExpandY: If true, create rays in both computational domain and expanded (by
reflection or translation in y direction) domain. If the created ray is in the expanded portion, then map the ray to the
computational domain.
- ed_createRaysExpandZ: If true, create rays in both computational domain and expanded (by
reflection or translation in z direction) domain. If the created ray is in the expanded portion, then map the ray to the
computational domain.
- ed_cubicInterpolationZeroDerv: If true, all cubic interpolation vertex derivatives
will be set equal to zero, enforcing monotonicity for interpolation between all vertices of a cell.
- ed_enforcePositiveNele: (AVG algorithm 18.4.4.1 only) If true, the x-, y- and
z-components of the gradients
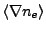 will be rescaled such that they always
deliver a positive (greater or equal zero) value for the number of electrons in a cell.
will be rescaled such that they always
deliver a positive (greater or equal zero) value for the number of electrons in a cell.
- ed_enforcePositiveTele: (AVG algorithm 18.4.4.1 only) If true, the x-, y- and
z-components of the gradients
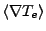 will be rescaled such that they always
deliver a positive (greater or equal zero) value for the electron temperature in a cell.
will be rescaled such that they always
deliver a positive (greater or equal zero) value for the electron temperature in a cell.
- ed_gradOrder: (AVG algorithm only) The order of approximation used
for the electron number density
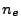 and the electron temperature
and the electron temperature 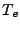 in a cell
(equation 18.39). A value of 1 leads to linear and a value of 2 to parabolic
(quadratic) ray trajectories inside the cell. The first case includes no gradients and only
takes the cell's average value.
in a cell
(equation 18.39). A value of 1 leads to linear and a value of 2 to parabolic
(quadratic) ray trajectories inside the cell. The first case includes no gradients and only
takes the cell's average value.
- ed_laser3Din2D: If true, 3D rays will be traced on a 2D cylindrical grid.
- ed_laser3Din2DwedgeAngle: The wedge opening angle
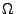 (in degrees)
for a 3D in 2D laser ray trace simulation.
(in degrees)
for a 3D in 2D laser ray trace simulation.
- ed_maxRayCount: The maximum number of rays that can be created on one
processor.
- ed_numberOfBeams: The number of laser beams that are going to be used.
- ed_numberOfPulses: Controls the number of different laser pulses that are
going to be used.
- ed_powerStepTolerance: (Cubic interpolation with Runge Kutta only) This
factor denotes the fractional error (unit = current power) for a Runge Kutta step in the CIRK
18.4.4.3 ray tracing method.
- ed_printBeams: If true, it prints detailed information about the laser
beams to a file with name
 basename
basename LaserBeamsPrint.txt, where
LaserBeamsPrint.txt, where  basename
basename is the base
name of the simulation.
is the base
name of the simulation.
- ed_printMain: If true, it prints general information regarding the laser
setup to a file with name
 basename
basename LaserMainDataPrint.txt, where
LaserMainDataPrint.txt, where  basename
basename is the base
name of the simulation.
is the base
name of the simulation.
- ed_printPulses: If true, it prints detailed information about the laser
pulses to a file with name
 basename
basename LaserPulsesPrint.txt, where
LaserPulsesPrint.txt, where  basename
basename is the base
name of the simulation.
is the base
name of the simulation.
- ed_printRays: If true, it prints detailed information about the all rays
initially generated on each processor to a file(s) with name(s)
 basename
basename LaserRaysPrint
LaserRaysPrint PID
PID .txt, where
.txt, where  basename
basename is the base name of the simulation
and PID is the processor rank number.
is the base name of the simulation
and PID is the processor rank number.
- ed_rayZeroPower: Below this value (erg/s), the ray is considered to have
zero power.
- ed_RungeKuttaMethod: (Cubic interpolation with Runge Kutta only) Specifies
which Runge Kutta method to use for the CIRK 18.4.4.3 ray tracing method.
Current options are: 'CashKarp45' (order 4, default), 'EulerHeu12' (order 1), 'BogShamp23' (order 2),
'Fehlberg34' (order 3) and 'Fehlberg45' (order 4).
- ed_saveOutOfDomainRays: If true, the rays info will be stored into a
separate saved ray array for those rays that exit the domain.
- ed_useRayCoords2GetBlockID: If true, the Grid Particles unit uses ray
coordinates to determine the new block ID when a ray exits a block. Otherwise block neighbor
info is used to determine the new block ID.
- ed_velocityStepTolerance: This factor times the current speed of a ray
in a cell is taken as the velocity component error tolerance for step-sized based ray tracing
methods.
- useEnergyDeposition: If false, the energy deposition is not activated,
even if the code was compiled to do so. Bypasses the need to rebuild the code.
- threadRayTrace: If true, the innermost ray loop, tracing all rays through
a block, is threaded. This runtime parameter can only be set during setup of the code.
Simulating 3D Cylindrical Laser Beam Intensities using 1D/2D Cartesian Grids:
Per implementation, in FLASH the concept of a cell volume for lower dimensional grids consists
in setting a unit length for each missing dimension. For example, in 1D cartesian, if a 1D cell
has length
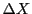
cm, then the corresponding cell volume as used in FLASH would be:
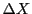
cm x 1 cm x 1cm =
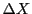
cm
. This results in different beam intensities when
using the same beam power for 1D/2D/3D cartesian laser simulations. To make these simulations
comparable with equal beam intensities, one can either adjust the individual beam powers or
one can use the same power and set the runtime parameter
ed_adjustBeamsTargetIntensity equal to true. The latter will then
internally determine the adjustment factor to be used for 1D/2D cartesian beams to emulate
a 3D cylindrical laser beam with radius equal to the beam's
ed_targetSemiAxisMajor.
In case one wants to adjust the 1D/2D cartesian beam powers (
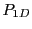
,
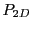
), the following
conversions should be used:
Simulating Axisymmetric Cylindrical Laser Beam Intensities using 1D Cylindrical Grids:
For these kind of simulations, the user needs to adjust the 1D cylindrical beam power by a
factor that mimics an axisymmetrical cylindrical laser beam. The beams
ed_targetSemiAxisMajor is now irrelevant, but instead the radial position
of the target and the laser intensity on target (
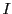
) should be considered. The 1D laser cylindrical beam power
(
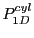
) should be given as:
where
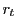
is the radial position of the target
ed_targetX.
18.4.11.4 LaserIO Runtime Parameters and Usage
Often times it is useful to be able to visualize the paths of the
individual rays in a simulation. This can be very helpful in ensuring
that the laser beams are set up in the intended manner. The LaserIO
directory in the source tree located at:
source/physics/sourceTerms/EnergyDeposition/EnergyDepositionMain/Laser/LaserIO
The LaserIO package gives users the ability to write the trajectory of
a certain number of rays to plot files when normal FLASH plot file
writes occur. This feature is only compatible with parallel HDF5 IO
implementations (for example, with +parallelIO or
+hdf5typeio). Only three runtime parameter options need to be
set to use LaserIO. These are:
- ed_useLaserIO: Set to .true. to activate LaserIO
- ed_laserIOMaxNumberOfRays: Sets the approximate maximum
number of rays to write to the plot file. This number can be less than the
total number of rays in the simulation. When greater than the
maximum number of rays, every ray trajectory is written.
- ed_laserIOMaxNumberOfPositions: Sets the size of the LaserIO
buffer. A good estimate of this value is
 .
.
The ed_laserIOMaxNumberOfRays parameter sets the approximate maximum number of rays to
write out. The exact number of rays that will be written is equal to:
where
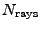 is the sum of the number of rays to launch for
each beam. The LaserIO ray information is written to the normal HDF5
plot files in the RayData dataset. The extract_rays.py
script that is distributed with FLASH in the tools/scripts
directory can be used to extract this data. This is a python script
which requires the NumPy and PyTables python packages to operate. The
script takes as arguments a list of plot files. For each plot file,
the script will generate a corresponding VTK file which can be loaded
into VisIt. The RayPower_Watts Pseudocolor in VisIt can be plotted to
show the ray trajectories. The rays are colored based on their power
(in watts). See the LaserSlab simulation Sec:LaserSlab
for an example which uses LaserIO.
is the sum of the number of rays to launch for
each beam. The LaserIO ray information is written to the normal HDF5
plot files in the RayData dataset. The extract_rays.py
script that is distributed with FLASH in the tools/scripts
directory can be used to extract this data. This is a python script
which requires the NumPy and PyTables python packages to operate. The
script takes as arguments a list of plot files. For each plot file,
the script will generate a corresponding VTK file which can be loaded
into VisIt. The RayPower_Watts Pseudocolor in VisIt can be plotted to
show the ray trajectories. The rays are colored based on their power
(in watts). See the LaserSlab simulation Sec:LaserSlab
for an example which uses LaserIO.
18.4.11.5 Laser Energy Density Output
Laser energy density (energy per volume - see 18.4.3) is very useful for visualizing lasers in the simulation space and can be output to the variable “lase” in checkpoint and plot files. This is an experimental feature in FLASH 4.4 and is implemented only for 3D Cartesian geometry. To enable “lase” output, edit your simulation's Config file (e.g., for the LaserSlab example, Simulation/SimulationMain/LaserSlab/Config) to include the line:
VARIABLE lase TYPE: PER_VOLUME
These unit tests set up a series of beams that launch rays onto a domain with a particular electron number
density and electron temperature distribution in such a way that an analytical solution is possible for the
ray paths and their power deposited inside the domain. The tests are 3D cartesian extensions to the 2D analytical
test solution for the quadratic trough as presented in the paper by Kaiser (2000). Figure 18.18
shows the basic structure. 2D cartesian versions of the tests is also available.
Figure:
One ray moving through an ellipsoidal tube with a
quadratic electron number density profile and reaching a focal point 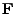 .
.
|
|
Let us define a quadratic ellipsoidal electron number density profile in a 3D space
along the xz-plane and having no variation along the y-axis:
Here 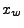 and
and 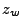 are the center coordinates of the ellipsoidal tube cross section,
are the center coordinates of the ellipsoidal tube cross section, 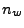 is the value of the electron number density at the center of the ellipse and
is the value of the electron number density at the center of the ellipse and 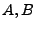 are the scaling
factors for the individual components. The values of
are the scaling
factors for the individual components. The values of 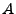 and
and  are determined by the boundary
conditions of
are determined by the boundary
conditions of
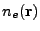 . For example, if one wants
. For example, if one wants
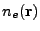 to be equal to a critical
value
to be equal to a critical
value 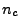 at specific coordinates
at specific coordinates 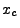 and (separately)
and (separately) 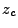 , then we have:
, then we have:
Using the ray equation of motion
we can solve for the position vector 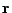 under several circumstances (boundary conditions).
The first thing to note is that
under several circumstances (boundary conditions).
The first thing to note is that
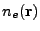 does not contain mixed variable terms, hence
the differential ray equation is separable into the individual components. Let us take the
x-component. We have
does not contain mixed variable terms, hence
the differential ray equation is separable into the individual components. Let us take the
x-component. We have
where
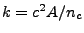 . This is the differential equation for a simple harmonic oscillator around the
point
. This is the differential equation for a simple harmonic oscillator around the
point 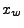 . The boundary conditions are such that at time
. The boundary conditions are such that at time  the ray will be at an initial
position
the ray will be at an initial
position 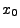 and will posses a certain velocity component
and will posses a certain velocity component 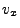
To solve the simple harmonic oscillator equation, we make the ansatz
and find the expressions for 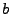 and
and 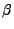 satisfying the boundary conditions. We have
satisfying the boundary conditions. We have
from which we deduce that
The solution to the complete ray equation can thus be stated as
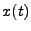 |
 |
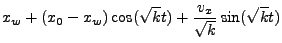 |
(18.221) |
 |
 |
 |
(18.222) |
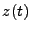 |
 |
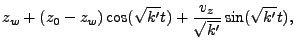 |
(18.223) |
where
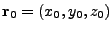 is the ray's initial position,
is the ray's initial position,
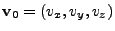 the
initial velocity and
the
initial velocity and
Let us now define a focal point 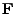 , where all rays launched will meet. The obvious choice is a
focal point along the tube's center line
, where all rays launched will meet. The obvious choice is a
focal point along the tube's center line 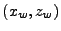 . Without specifying the y-coordinate of this
point yet, we ask the question: at what times
. Without specifying the y-coordinate of this
point yet, we ask the question: at what times 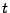 and
and 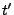 will
will 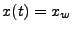 and
and 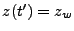 for the
first time after launch? From the ray equation solutions we get
for the
first time after launch? From the ray equation solutions we get
where the angular region of interest for the tangent is
 . It is interesting that
there is both a lower and an upper limit to these times. While the lower limit of
. It is interesting that
there is both a lower and an upper limit to these times. While the lower limit of
 makes sense (if we shoot the ray with infinite velocity towards the tube's center) the upper limit
of
makes sense (if we shoot the ray with infinite velocity towards the tube's center) the upper limit
of
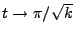 is less intuitive: there is no escape from the tube no matter what
initial outward velocity we give the ray due to increasing pulling back force towards the center as the ray
moves away from it. If the velocity component is zero we have
is less intuitive: there is no escape from the tube no matter what
initial outward velocity we give the ray due to increasing pulling back force towards the center as the ray
moves away from it. If the velocity component is zero we have
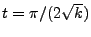 .
.
In general, both times  and
and  will be different. What this means is that the ray will not
hit the focal point. For that to occur, both times must be equal, hence we must have
will be different. What this means is that the ray will not
hit the focal point. For that to occur, both times must be equal, hence we must have
Given 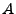 and
and  values (and thus
values (and thus 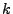 and
and 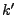 values via equations 18.224 and 18.225)
defining the tube's electron number density layout, this last relation imposes a condition
among the variables
values via equations 18.224 and 18.225)
defining the tube's electron number density layout, this last relation imposes a condition
among the variables
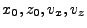 . Only if this condition is fulfilled will a focal point
at
. Only if this condition is fulfilled will a focal point
at
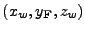 be reached. The y-coordinate
be reached. The y-coordinate 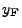 of the focal point is then obtained
from the y-solution 18.222 of the ray equation by inserting the value of the time
of the focal point is then obtained
from the y-solution 18.222 of the ray equation by inserting the value of the time 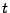 obtained
through either side of 18.228. For the unit test we must identify
obtained
through either side of 18.228. For the unit test we must identify 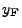 to be
sitting on the domain boundary. Hence when launching a series of ray's for the unit test, all
to be
sitting on the domain boundary. Hence when launching a series of ray's for the unit test, all 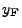 must be the same. A first scheme I thus emerges for setting up a very general unit test:
must be the same. A first scheme I thus emerges for setting up a very general unit test:
SCHEME I
- Fix the center
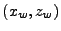 of the ellipsoidal tube cross section, set up the x- and z-dimensions
of the domain, and assign a value to the electron number density
of the ellipsoidal tube cross section, set up the x- and z-dimensions
of the domain, and assign a value to the electron number density 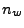 at the center.
at the center.
- Set up the ellipsoidal tube parameters
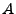 and
and  , as shown in 18.210 and
18.211, and choose a constant
, as shown in 18.210 and
18.211, and choose a constant 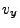 velocity component.
velocity component.
- For one trial ray, given the initial position and velocity x-components
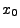 and
and 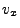 , determine
the time
, determine
the time 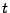 to reach the focal point
to reach the focal point 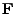 using equation 18.226.
using equation 18.226.
- Using
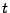 and
and 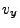 , calculate
, calculate 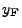 from 18.222, and set up the y-dimensions of the domain.
from 18.222, and set up the y-dimensions of the domain.
- Set up the initial x-component positions
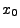 for the whole set of rays that are going to be launched.
for the whole set of rays that are going to be launched.
- Using
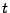 , determine the corresponding x-component velocities
, determine the corresponding x-component velocities 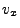 for all rays from
equation 18.226.
for all rays from
equation 18.226.
- For each ray, choose a
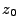 location and determine the needed velocity component
location and determine the needed velocity component 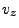 using
the relation 18.228.
using
the relation 18.228.
- Launch all rays and collect all the x- and z-components of the domain exit points
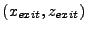 .
.
- For each ray, check how close
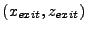 is to the expected
is to the expected 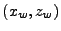 .
.
A second simplified scheme II (and the one that is currently implemented in FLASH) has all rays launched
vertically onto the xz-face of the domain. This means that 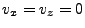 . By looking at the time
condition 18.228, we see that the only possibility for a focal point in this
case is if
. By looking at the time
condition 18.228, we see that the only possibility for a focal point in this
case is if 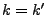 , and the time associated with it is equal to
, and the time associated with it is equal to
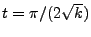 . This means
that we must have
. This means
that we must have 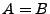 (a circular tube). Scheme II is set up as follows:
(a circular tube). Scheme II is set up as follows:
SCHEME II
- Fix the center
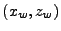 of the circular tube cross section, set up the x- and z-dimensions
of the domain, and assign a value to the electron number density
of the circular tube cross section, set up the x- and z-dimensions
of the domain, and assign a value to the electron number density 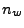 at the center.
at the center.
- Set up the circular tube parameter
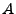 , as shown in 18.210, and choose
a constant
, as shown in 18.210, and choose
a constant 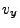 velocity component.
velocity component.
- Calculate the time
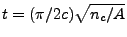 to reach the focal point
to reach the focal point  .
.
- Using
 and
and 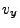 , calculate
, calculate 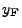 from 18.222, and set up the y-dimensions of the domain.
from 18.222, and set up the y-dimensions of the domain.
- Set up the initial positions
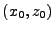 for the whole set of rays that are going to be launched.
for the whole set of rays that are going to be launched.
- Launch all rays and collect all the x- and z-components of the domain exit points
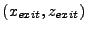 .
.
- For each ray, check how close
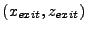 is to the expected
is to the expected 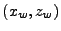 .
.
Note, that for scheme II there is no restriction on the initial ray positions 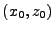 like in
scheme I. Rays launched vertically from anywhere onto the xz-plane with the same
like in
scheme I. Rays launched vertically from anywhere onto the xz-plane with the same 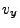 velocity will reach the
same focal point
velocity will reach the
same focal point 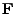 . Their paths might be of different lengths, but the time it takes for
them to reach
. Their paths might be of different lengths, but the time it takes for
them to reach 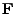 is always the same.
is always the same.
According to equation 18.47, the power remaining after the ray exits the ellipsoidal tube
is
where 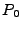 and
and 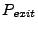 denote the ray's power at the tube's entry and exit point and
denote the ray's power at the tube's entry and exit point and 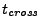 is
the time it takes for the ray to reach the focal point
is
the time it takes for the ray to reach the focal point 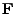 . From 18.46, the
inverse-Bremsstrahlung rate is
. From 18.46, the
inverse-Bremsstrahlung rate is
Note the dependence of 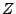 on position, since we are dealing with the entire domain and not with
individual cells. In order to obtain an analytical integrand that is easy to integrate, the first
assumption that we make is that both
on position, since we are dealing with the entire domain and not with
individual cells. In order to obtain an analytical integrand that is easy to integrate, the first
assumption that we make is that both 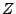 and
and 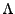 are independent of position. For convenience
we chose:
are independent of position. For convenience
we chose:
To change the quadratic dependence on the electron number density to a linear dependency, we set
the electron temperature as
with a specific electron temperature 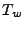 at the elliptical origin. Using these choices we obtain
at the elliptical origin. Using these choices we obtain
where
is the inverse-Bremsstrahlung rate at the origin. The integral in the exponential becomes
Inserting the analytical path solutions 18.221 and 18.223, we can perform
the integration. Let us concentrate on the x-component part only. We are lead to an integral of
the form
where 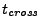 is given by the expression in 18.226. For this integration, known sine
and cosine integration rules have been used as well as the fact that
is given by the expression in 18.226. For this integration, known sine
and cosine integration rules have been used as well as the fact that
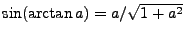 and
and
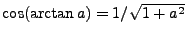 . The z-component integration is similar. Collecting
everything together and using the expressions for
. The z-component integration is similar. Collecting
everything together and using the expressions for 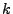 ,
,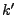 ,
,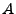 and
and  from 18.224, 18.225,
18.210 and 18.211 we obtain
from 18.224, 18.225,
18.210 and 18.211 we obtain
This is the general expression of the exponent integral for evaluating the power deposition of the
rays for scheme I. For the circular tube of scheme II we have 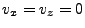 ,
,
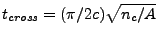 ,
,
 , and the exponent integral simplifies to
, and the exponent integral simplifies to
If all rays start with the same power and imposing equal power deposition for all rays, then the term
inside the curly brackets must be equal to a constant value
This condition implies that the rays have to be launched on a circle with radius  around the tube
origin
around the tube
origin 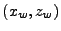 . This ensures equal path lengths for all rays and hence equal power deposition.
. This ensures equal path lengths for all rays and hence equal power deposition.
The current Energy Deposition unit test coded into FLASH is based on the analytic solutions for scheme II.
The circular quadratic potential tube is defined through the following parameters and constants:
| Parameters |
Constants in FLASH |
= | |
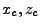 |
= | 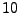 cm cm |
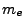 |
= |
 g g |
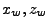 |
= | 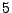 cm cm |
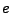 |
= |
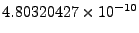 esu esu |
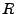 |
= | 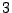 cm cm |
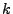 |
= |
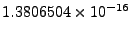 erg/K erg/K |
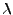 |
= |
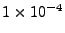 cm cm |
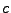 |
= |
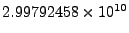 cm/sec cm/sec |
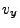 |
= | 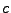 |
|
|
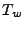 |
= |  keV keV |
|
|
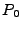 |
= | 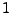 erg/sec erg/sec |
|
|
With these values we obtain the following additional variable values (in parenthesis are the
equations used), completing the picture:
Evaluation of each cell's average electron number density is done by integrating equation
18.209 over the entire cell xz-area
where 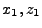 are the lower and
are the lower and 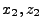 the upper corresponding cell edge coordinates and
the upper corresponding cell edge coordinates and
with corresponding equations for the z-part. The average cell's electron temperature is evaluated directly
from the average electron number density using 18.233
The gradients are obtained from the cell average values using the symmetrized derivative formula
(shown here for the 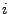 -th cell x-component of the electron number density gradient)
-th cell x-component of the electron number density gradient)
where
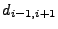 is twice the distance between neighboring cells on the x-axis.
is twice the distance between neighboring cells on the x-axis.
TEST I
For test I, a series of 8 rays (from 8 beams with 1 ray each) with radial distances of  from
from
 are launched with the following initial
are launched with the following initial 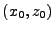 coordinates (all in cm):
coordinates (all in cm):
Results are shown only for the ray 1 and ray 5, the other ones are related to these two by symmetry.
Also 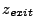 is not given, because for ray 1 we have
is not given, because for ray 1 we have
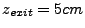 and for ray 5 we have
and for ray 5 we have
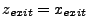 . The percentage errors were calculated as
. The percentage errors were calculated as
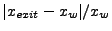 and likewise for
the power deposition.
and likewise for
the power deposition.
| Refinement Level |
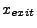 |
% error |
 |
% error |
| Ray 1 |
| 1 |
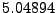 |
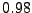 |
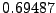 |
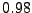 |
| 2 |
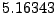 |
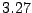 |
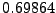 |
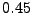 |
| 3 |
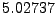 |
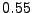 |
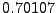 |
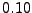 |
| 4 |
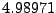 |
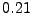 |
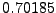 |
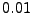 |
| 5 |
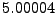 |
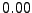 |
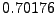 |
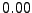 |
| 6 |
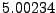 |
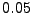 |
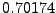 |
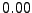 |
| Ray 5 |
| 1 |
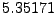 |
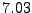 |
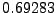 |
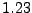 |
| 2 |
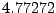 |
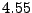 |
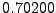 |
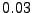 |
| 3 |
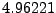 |
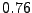 |
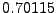 |
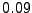 |
| 4 |
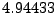 |
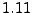 |
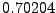 |
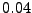 |
| 5 |
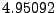 |
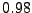 |
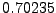 |
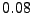 |
| 6 |
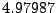 |
 |
 |
 |
| Analytical |
 |
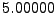 |
|
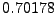 |
|
TEST II
The second test is also based on scheme II and aims at launching a large number of rays using only one beam centered
along the tube's origin with a specific cross section power function, such that all rays reaching the focal point
have an equal exit power. Since the power deposited depends on the ray path length, the cross section power function
must be such that each ray gets the appropriate initial power to account for the differences in path lengths. For a
specific ray we have for the exit power
where equations 18.239, 18.229 and 18.108 have been used
and
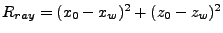 is the ray's radial distance from the tube origin. If we set the ray weighting
function equal to the inverse gaussian function
is the ray's radial distance from the tube origin. If we set the ray weighting
function equal to the inverse gaussian function
we obtain
where we have used 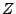 for the power partition function
for the power partition function
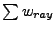 . For a particular number of rays per beam,
. For a particular number of rays per beam,
 is constant and therefore the exit power of all rays are equal. To get independent of the number of rays,
the unit test records the partition scaled exit power
is constant and therefore the exit power of all rays are equal. To get independent of the number of rays,
the unit test records the partition scaled exit power
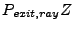 for each ray as well as their focal
for each ray as well as their focal
 coordinates. A maximum square radial deviation
coordinates. A maximum square radial deviation
from the focal point is then defined and recorded. The maximum absolute deviation in the partition scaled power
is registered as
Both quantities are then checked against tolerance values.
In these unit tests a ring of laser rays is shot on to a 3D cylindrical can and their domain
exit properties are recorded and analyzed.
This test reveals how well a straight line movement by the rays is maintained in 3D
cylindrical coordinates. As rays enter the 3D cylindrical domain, their radial and
tangential angular velocity change continuously along their straight line path through
the can. On exit the laser ring should have the same radius as on entry and all rays
should have the same initial speed, with deviations depending on the domain refinement
level. Figure 18.19 shows schematically the unit test.
Figure 18.19:
Schematic drawing of the incident laser ring on
the mantle of a 3D cylindrical can with no domain ray acceleration. Linear path of a ray
through the 3D cylindrical domain blocks/cells is also shown.
|
|
The 3D cylindrical can is specified by the following domain min/max coordinates:
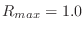 cm,
cm,
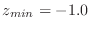 cm and
cm and
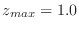 cm. The laser ring consists
of
cm. The laser ring consists
of 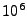 rays, has a radius of
rays, has a radius of 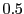 cm and is shot along the 3D cartesian
cm and is shot along the 3D cartesian  direction
on the mantle center at
direction
on the mantle center at 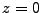 cm. Each ray carries a power of 1 erg/s. A uniform electron
number density (half the critical density) is set throughout the can to ensure no radial
and angular acceleration. Speed adjustment of the rays as they enter the domain is supressed,
hence all rays will travel with the speed of light
cm. Each ray carries a power of 1 erg/s. A uniform electron
number density (half the critical density) is set throughout the can to ensure no radial
and angular acceleration. Speed adjustment of the rays as they enter the domain is supressed,
hence all rays will travel with the speed of light 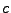 through the can. A uniform inverse
Bremsstrahlungsrate of
through the can. A uniform inverse
Bremsstrahlungsrate of
is used, to accomplish a power reduction by 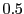 for those rays that travel with the
speed of light the full diameter of 2 cm of the can. In the top view of Figure
18.19, we denote by
for those rays that travel with the
speed of light the full diameter of 2 cm of the can. In the top view of Figure
18.19, we denote by  half the distance traveled by the
ray inside the can. Hence the ray travels
half the distance traveled by the
ray inside the can. Hence the ray travels 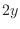 cm through the can in
cm through the can in 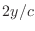 seconds
and for this ray an exit power reduction of
seconds
and for this ray an exit power reduction of
is expected. The unit test collects three relative quantities (exit value / expected value)
for each ray: 1) the ring radius, 2) the ray speed and 3) the ray power. Min/max of these
relative quantities are then formed over all rays and deviations from 1 are checked against
a predefined benchmark for passing the test.
An additional test is being done to see if the laser ring retained its shape while entering
and traveling through the can. On creation in the beam, all rays of the laser ring are placed
uniformly on the ring with equal separation among each other. On exit from the can the rays
should still be uniformly spaced in their angular position. Since checking for nearest neighbor
rays for each ray is in our case a
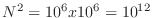 process, we resort to a simpler
method. We define an angular tic
process, we resort to a simpler
method. We define an angular tic
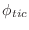 value as the minimum angular separation of each
ray in the beam:
value as the minimum angular separation of each
ray in the beam:
On exit from the can, the angular position variable 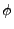 of each ray is divided by
of each ray is divided by
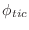 and the nearest integer is formed, giving the label
and the nearest integer is formed, giving the label 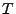 of a tic in which the ray
would be found:
of a tic in which the ray
would be found:
If the laser ring retained its shape, then there should be only 1 ray for each tic, i.e. the
list of labels 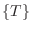 should consist of consecutive natural numbers, which can
easily be checked by defining a zero tic array and adding 1 to each tic whenever a ray is found
to belong to it. A final tic array containing only 1's indicates success in retaining the original
laser ring shape. Since straight line movement in 3D cylindrical coordinates is a considerable
stress test for the code, we allow a maximum tic occupancy of 2 (and hence a tic occupancy of 0
for other tics) for this test to succeed.
should consist of consecutive natural numbers, which can
easily be checked by defining a zero tic array and adding 1 to each tic whenever a ray is found
to belong to it. A final tic array containing only 1's indicates success in retaining the original
laser ring shape. Since straight line movement in 3D cylindrical coordinates is a considerable
stress test for the code, we allow a maximum tic occupancy of 2 (and hence a tic occupancy of 0
for other tics) for this test to succeed.
The purpose of this test is to check proper ray crossing at the 3D cylindrical axis.
The laser ring contracts towards the axis in a singular point at 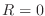 and expands
afterwards regaining its original shape. On exit the laser ring should have the same
radius as on entry and all rays should have the same initial speed, which increases
towards the singular point when the ring contracts and decreases afterwards when the
ring expands. Inside the can the laser ring traces an hourglass shape with a single
point at its center.
and expands
afterwards regaining its original shape. On exit the laser ring should have the same
radius as on entry and all rays should have the same initial speed, which increases
towards the singular point when the ring contracts and decreases afterwards when the
ring expands. Inside the can the laser ring traces an hourglass shape with a single
point at its center.
The 3D cylindrical can is specified by the following domain min/max coordinates:
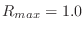 cm,
cm,
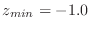 cm and
cm and
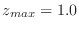 cm. The laser ring consists
of
cm. The laser ring consists
of 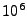 rays, has a radius of
rays, has a radius of 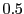 cm and is shot along the 3D cartesian
cm and is shot along the 3D cartesian 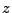 direction
on the lid center at
direction
on the lid center at 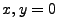 cm. Each ray carries a power of 1 erg/s. A linear electron
number density gradient
cm. Each ray carries a power of 1 erg/s. A linear electron
number density gradient
is set throughout the can to ensure a uniform radial acceleration of (from Eq.(18.161)
and using
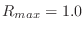 )
)
towards the 3D cylindrical axis. As the initial radial velocity 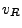 is zero, the time it
takes for each ray to exit the can on the opposite lid is equal to twice the time it takes
for it to reach the axis at
is zero, the time it
takes for each ray to exit the can on the opposite lid is equal to twice the time it takes
for it to reach the axis at 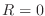 :
:
Using a uniform inverse Bremsstrahlungsrate of
the power reduction rate for each ray at exit is
In order for the rays not to exceed the speed of light inside the can, initial ray speed
adjustment is set true, with each ray entering the can at 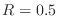 with an axial velocity of:
with an axial velocity of:
At the axis, the rays will have gained a radial velocity of
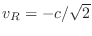 due to the
radial acceleration. On exit the radial velocity is again
due to the
radial acceleration. On exit the radial velocity is again 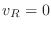 , while the axial velocity
remains unchanged. The speed of each ray at the axis and at the exit point will therefore be:
, while the axial velocity
remains unchanged. The speed of each ray at the axis and at the exit point will therefore be:
The unit test collects three relative quantities at the exit point (exit value / expected value)
for each ray: 1) the ring radius, 2) the ray speed and 3) the ray power. Min/max of these
relative quantities are then formed over all rays and deviations from 1 are checked against
a predefined benchmark for passing the test. Since pure radial movement of the rays is
considerably easier in 3D cylindrical coordinates when compared to straight line movements,
the laser ring shape test is only successful, if all tics are strictly occupied only once.
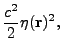
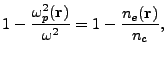
![]() of an electromagnetic wave is depleted by the inverse Bremsstrahlung (ib) process.
The rate of power loss is governed by a 1st order ordinary differential equation (ODE):
of an electromagnetic wave is depleted by the inverse Bremsstrahlung (ib) process.
The rate of power loss is governed by a 1st order ordinary differential equation (ODE):
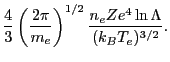
![$\displaystyle \ln \left[\frac{3}{2Ze^3}\left(\frac{k_B^3T_e^3}{\pi n_e}\right)^{1/2}\right].$](img1157.png)
![$\displaystyle \ln \Lambda[{\bf r}_0] =
\ln \left[\frac{3}{2Ze^3}\left(\frac{k^3T_e({\bf r}_0)^3}{\pi n_e({\bf r}_0)}\right)^{1/2}\right].$](img1164.png)
![$\displaystyle n_e({\bf r}_0) \left[1 + \frac{\nabla n_e({\bf r}_0) \cdot {\bf v...
...bla n_e({\bf r}_0) \cdot \nabla n_e({\bf r}_0)}{4n_cn_e({\bf r}_0)} t^2 \right]$](img1169.png)
![$\displaystyle T_e({\bf r}_0) \left[1 + \frac{\nabla T_e({\bf r}_0) \cdot {\bf v...
...la T_e({\bf r}_0) \cdot \nabla n_e({\bf r}_0)}{4n_cT_e({\bf r}_0)} t^2 \right].$](img1170.png)
![$\displaystyle \frac{4}{3} \left (\frac{2 \pi}{m_e} \right)^{1/2}
\frac{Z e^4 \ln \Lambda[{\bf r}_0]}{n_ck^{3/2}}
\frac{n_e({\bf r}_0)^2}{T_e({\bf r}_0)^{3/2}}$](img1175.png)
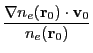
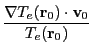
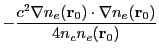
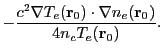
![]() with power
with power ![]() through an area
through an area ![]() has an energy density of
has an energy density of
![]() .
.
![]() changes along the ray path by Eq.(18.47). For light traveling at speed
changes along the ray path by Eq.(18.47). For light traveling at speed ![]() (determined by frequency and medium), ray linear energy density
(determined by frequency and medium), ray linear energy density ![]() similarly varies along ray path:
similarly varies along ray path:
![]() is found by integrating linear energy density
is found by integrating linear energy density ![]() over the ray's path within the cell (
over the ray's path within the cell (![]() is the parametrized time value for which the ray reaches edge of cell), then dividing by cell volume
is the parametrized time value for which the ray reaches edge of cell), then dividing by cell volume ![]() :
:
![]() ) are summed to give a total laser energy density for that cell.
) are summed to give a total laser energy density for that cell.
![]() and electron temperature
and electron temperature
![]() value at the center of the cell. The electron number density gradient vector
value at the center of the cell. The electron number density gradient vector
![]() as
well as the electron temperature gradient vector
as
well as the electron temperature gradient vector
![]() are assumed to be constant within each cell. Rays will be transported through each cell between cell faces
in one step. Electron number densities
are assumed to be constant within each cell. Rays will be transported through each cell between cell faces
in one step. Electron number densities ![]() and electron temperatures
and electron temperatures ![]() on the entry cell face are
calculated from the cell center values in accordance with equation 18.39 using first order
Taylor expansions
on the entry cell face are
calculated from the cell center values in accordance with equation 18.39 using first order
Taylor expansions
![]() and
and
![]() replaced by their cell average values
replaced by their cell average values
![]() and
and
![]() and
and
![]() and
and
![]() replaced by their corresponding cell entry values
replaced by their corresponding cell entry values ![]() and
and ![]() .
The upper integration time limit is
.
The upper integration time limit is ![]() , the ray's cell crossing time.
, the ray's cell crossing time.
![]() at the
cell interfaces. To account for this,
the ray undergoes refraction according to Snell's law. Refraction at cell interfaces causes a
change in the ray's velocity normal to the interface surface while preserving the ray velocity
component transverse to the interface normal. To derive the change in the ray normal velocity
component, imagine the cell interface to have a small infinitesimal thickness
at the
cell interfaces. To account for this,
the ray undergoes refraction according to Snell's law. Refraction at cell interfaces causes a
change in the ray's velocity normal to the interface surface while preserving the ray velocity
component transverse to the interface normal. To derive the change in the ray normal velocity
component, imagine the cell interface to have a small infinitesimal thickness ![]() and the ray moving
from left to right through the interface. On the left and right the normal velocity components are
and the ray moving
from left to right through the interface. On the left and right the normal velocity components are
![]() and
and ![]() , respectively, while the corresponding
, respectively, while the corresponding ![]() are
are ![]() and
and ![]() .
Since we are dealing with an interface of infinitesimal thickness, we can use the first order
equation 18.40 to get
.
Since we are dealing with an interface of infinitesimal thickness, we can use the first order
equation 18.40 to get
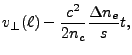
![]() and
and ![]() representations as
well as continuous first derivatives
representations as
well as continuous first derivatives
![]() and
and
![]() throughout the entire domain. This allows
for the calculation of a more smoother path for each ray inside each cell when compared to the AVG algorithm.
In effect, the cell-by-cell choppiness of the AVG algorithm can be avoided by taking many small ray
steps inside each cell. Also, the troublesome
throughout the entire domain. This allows
for the calculation of a more smoother path for each ray inside each cell when compared to the AVG algorithm.
In effect, the cell-by-cell choppiness of the AVG algorithm can be avoided by taking many small ray
steps inside each cell. Also, the troublesome ![]() discontinuities at the cell boundaries and the
application of Snell's law will disappear. The essential features of the cubic interpolation schemes are
layed out in section 32.2. In what follows we show the piecewise parabolic ray tracing scheme.
discontinuities at the cell boundaries and the
application of Snell's law will disappear. The essential features of the cubic interpolation schemes are
layed out in section 32.2. In what follows we show the piecewise parabolic ray tracing scheme.
![]() and
and ![]() at the Gaussian quadrature points are evaluated using the cubic interpolation
equation Eq.(32.11). The following scheme illustrates the steps involved for tracing a
ray through a cell, assuming the ray is somewhere located in the cell at
at the Gaussian quadrature points are evaluated using the cubic interpolation
equation Eq.(32.11). The following scheme illustrates the steps involved for tracing a
ray through a cell, assuming the ray is somewhere located in the cell at ![]() with velocity
with velocity ![]() :
:
![]() . The curve of
. The curve of ![]() gives the power of the laser pulse
at any given simulation time. In FLASH, the form of
gives the power of the laser pulse
at any given simulation time. In FLASH, the form of ![]() is given by a series of points, which are
connected via straight lines (see Figure 18.5).
is given by a series of points, which are
connected via straight lines (see Figure 18.5).
![]() , and hits the target,
whose center is located at
, and hits the target,
whose center is located at ![]() . In 3D geometries, the elliptical target area is defined as
an ellipse perpendicular to the lens-target line and whose largest semiaxis
. In 3D geometries, the elliptical target area is defined as
an ellipse perpendicular to the lens-target line and whose largest semiaxis ![]() is positioned
such that it makes a torsional angle
is positioned
such that it makes a torsional angle ![]() with the local target z-axis (see Figure 18.6).
Let us define the beam vector
with the local target z-axis (see Figure 18.6).
Let us define the beam vector
![]() pointing from the target to the lens
and connecting the two respective centers. We then have the defining equations
for
pointing from the target to the lens
and connecting the two respective centers. We then have the defining equations
for ![]()
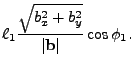
![$\displaystyle \frac{\ell_1}{\sqrt{b_x^2+b_y^2}}
\left[- \frac{b_x b_z}{\vert{\bf b}\vert} \cos \phi_1 \pm b_y \sin \phi_1 \right]$](img1291.png)
![$\displaystyle \frac{\ell_1}{\sqrt{b_x^2+b_y^2}}
\left[- \frac{b_y b_z}{\vert{\bf b}\vert} \cos \phi_1 \mp b_x \sin \phi_1 \right]$](img1293.png)
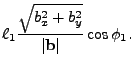
![$\displaystyle \frac{1}{\sqrt{b_x^2+b_y^2}}
\left[\frac{b_x b_z}{\vert{\bf b}\vert} \sin \phi_1 - b_y \cos \phi_1 \right]$](img1306.png)
![$\displaystyle \frac{1}{\sqrt{b_x^2+b_y^2}}
\left[\frac{b_y b_z}{\vert{\bf b}\vert} \sin \phi_1 + b_x \cos \phi_1 \right]$](img1308.png)
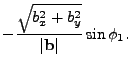
![]() . The components of the unit vector
can be deduced from the equations 18.77 and 18.78 as
. The components of the unit vector
can be deduced from the equations 18.77 and 18.78 as
![]() and target
and target ![]() positions, both
elliptical target zone semiaxes lengths
positions, both
elliptical target zone semiaxes lengths ![]() and
and ![]() , the first semiaxis torsion
angle
, the first semiaxis torsion
angle ![]() and the coordinate axis to which
and the coordinate axis to which ![]() refers to. We wish to enforce in the
code a complete containment of the entire target plane inside the domain boundaries. To check
this condition we need the extremum coordinate values of the elliptical boundary curve of the
target. The collection of all points
refers to. We wish to enforce in the
code a complete containment of the entire target plane inside the domain boundaries. To check
this condition we need the extremum coordinate values of the elliptical boundary curve of the
target. The collection of all points ![]() , based on the local target coordinate system,
can be given in the following implicit form
, based on the local target coordinate system,
can be given in the following implicit form
![]() and
and
![]() . From the definition of the trigonometric functions based
on the length of the three sides of a right-angled triangle (a = opposite side, b =
adjacent side, c = hypotenuse for an angle
. From the definition of the trigonometric functions based
on the length of the three sides of a right-angled triangle (a = opposite side, b =
adjacent side, c = hypotenuse for an angle ![]() ), we have, using
), we have, using
![]() ,
,
![]() ,
,
![]() and
and
![]()
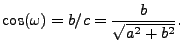
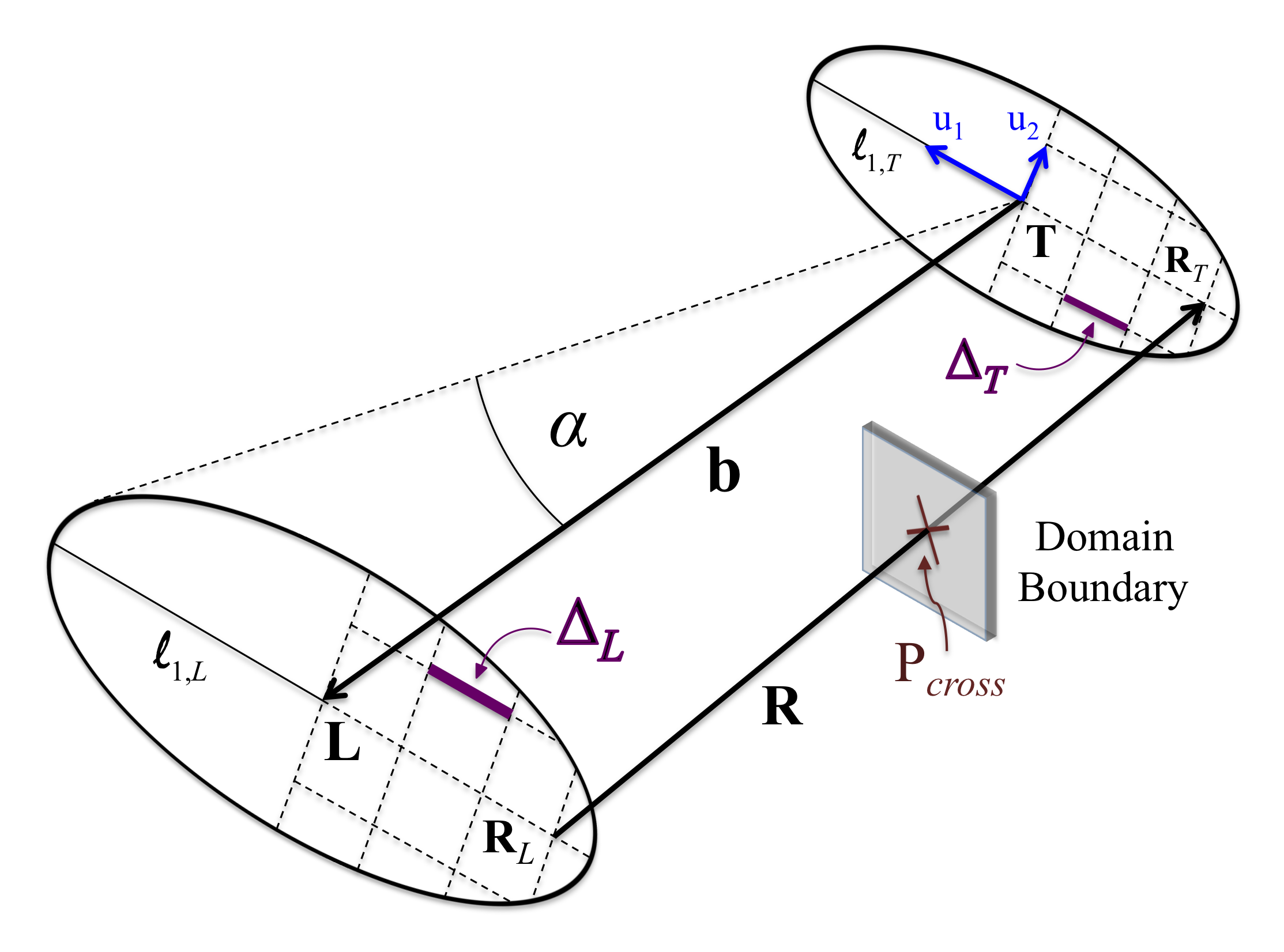
![]() ,
we can set up a square grid inside the ellipse, such that the number of grid intersection
points matches closely the number of rays
,
we can set up a square grid inside the ellipse, such that the number of grid intersection
points matches closely the number of rays ![]() specified by the user. The grid is defined by
the separation
specified by the user. The grid is defined by
the separation ![]() between two grid points and the placement of the grid's origin at the
center of the ellipse. Our goal is to find this
between two grid points and the placement of the grid's origin at the
center of the ellipse. Our goal is to find this ![]() value.
value.
![]() the number of grid intersection points for the circumscribing rectangle with
sides
the number of grid intersection points for the circumscribing rectangle with
sides ![]() and
and ![]() . We then have
. We then have
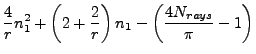
![]() , the next task is to find the optimum (or close to optimum) grid spacing
, the next task is to find the optimum (or close to optimum) grid spacing ![]() . This
is done by defining a minimum and maximum grid spacing value
. This
is done by defining a minimum and maximum grid spacing value
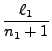
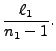
![]() and
and ![]() semiaxes are specified by the user, the
semiaxes are specified by the user, the ![]() for
the target square grid is evaluated using the above algorithm. The corresponding lens
for
the target square grid is evaluated using the above algorithm. The corresponding lens ![]() value is set using the similarity in size between the lens and the target. Using the user's
specified
value is set using the similarity in size between the lens and the target. Using the user's
specified ![]() for the lens, the preservation of length relations between similar objects
leads to:
for the lens, the preservation of length relations between similar objects
leads to:
![]() pair and the number of tics on the angle
pair and the number of tics on the angle ![]() within the range
within the range
![]() . The number
of tics on both of these 'axes' will be the same and will be denoted by
. The number
of tics on both of these 'axes' will be the same and will be denoted by ![]() . The total number of radial
grid points within the lens and target ellipses will be equal to
. The total number of radial
grid points within the lens and target ellipses will be equal to ![]() , leading to the quadratic
equation
, leading to the quadratic
equation
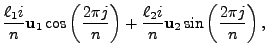
![]() and
and
![]() and rescaling by the ellipse/rectangle area factor. If we denote the user supplied tic separations
corresponding to the
and rescaling by the ellipse/rectangle area factor. If we denote the user supplied tic separations
corresponding to the ![]() semiaxis and
semiaxis and ![]() semiaxis by
semiaxis by ![]() and
and ![]() , then the
estmated number of rays would be:
, then the
estmated number of rays would be:
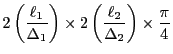
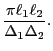
![]() and
and
![]() . The grid center
. The grid center
![]() is thus not part of the delta grid.
is thus not part of the delta grid.
![]() pairs within the
range
pairs within the
range ![]() , where the
, where the ![]() and
and ![]() denote fractions of the
denote fractions of the ![]() and
and ![]() semiaxis. A
random number generator for the range
semiaxis. A
random number generator for the range ![]() is used and the numbers are shifted to the
is used and the numbers are shifted to the
![]() range by multiplying by 2 and adding
range by multiplying by 2 and adding ![]() . Every
. Every ![]() pair is checked, if it actually
lays within the ellipse and retained if it does. The random
pair is checked, if it actually
lays within the ellipse and retained if it does. The random ![]() pair generation stops,
once the requested number of rays is reached. In order to use different statistical grids
for each time step, the statistical grid is regenerated afresh for each time step using a different
random seed value.
pair generation stops,
once the requested number of rays is reached. In order to use different statistical grids
for each time step, the statistical grid is regenerated afresh for each time step using a different
random seed value.
![]() and
and ![]() target coordinate system located at the center of the beam, the
gaussian weighting function for 2D target areas (3D geometries) reads
target coordinate system located at the center of the beam, the
gaussian weighting function for 2D target areas (3D geometries) reads
![$\displaystyle \exp^{{\displaystyle -\left[\left(\frac{x}{R_x}\right)^2\right]}^{\displaystyle \gamma}}.$](img1403.png)
![]() and a local target elliptical coordinate pair
and a local target elliptical coordinate pair ![]() .
The corresponding global coordinates can be obtained using the global lens and target center
coordinates and the elliptical unit vectors (see Figure 18.7)
.
The corresponding global coordinates can be obtained using the global lens and target center
coordinates and the elliptical unit vectors (see Figure 18.7)
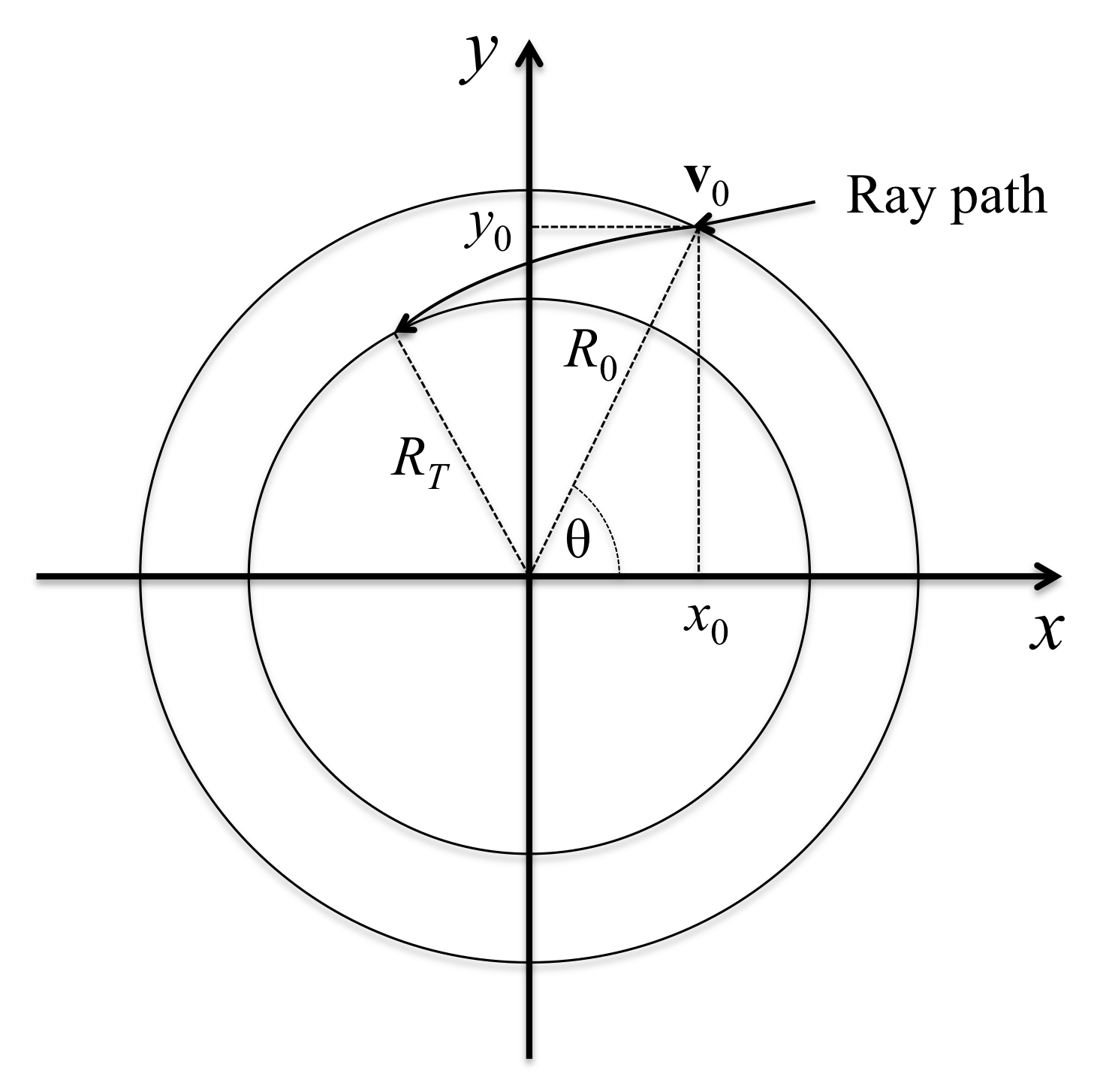
![]() moving in a central force
environment with no external forces acting on it. The motion of such an object is characterized by
constant energy and angular momentum and is hence confined to a 2D plane. There are two ways to describe the position
moving in a central force
environment with no external forces acting on it. The motion of such an object is characterized by
constant energy and angular momentum and is hence confined to a 2D plane. There are two ways to describe the position
![]() , velocity
, velocity ![]() and acceleration
and acceleration ![]() vectors of a particle in a 2D plane: using cartesian
vectors of a particle in a 2D plane: using cartesian
![]() or polar
or polar
![]()
![]() unit vectors.
They are interrelated by
unit vectors.
They are interrelated by
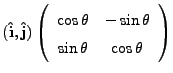
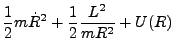
![$\displaystyle \int_{R_0}^{R_T}\left[\frac{2}{m}(E-U(R))-\frac{L^2}{m^2R^2}\right]^{-1/2}dR$](img1455.png)
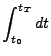
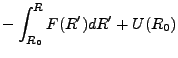
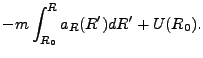
![$\displaystyle \int_{R_0}^{R_T}\left[\frac{2E}{m}-\frac{L^2}{m^2R^2}+2a(R-R_0)\right]^{-1/2}dR,$](img1468.png)
![]() polar variable
describing the rotational symmetry. An approximate treatment can be formulated, in which
each circle is treated as a linear polygon with
polar variable
describing the rotational symmetry. An approximate treatment can be formulated, in which
each circle is treated as a linear polygon with ![]() sides (
sides (![]() not necessarily integer), where
the value of
not necessarily integer), where
the value of ![]() determines the quality of the approximation. The exact 3D radial acceleration cylindrical
problem in
determines the quality of the approximation. The exact 3D radial acceleration cylindrical
problem in
![]() coordinates is transformed into an approximate 3D cartesian problem in
coordinates is transformed into an approximate 3D cartesian problem in
![]() coordinates, where the
coordinates, where the ![]() coordinate remains unaffected. Each torus cell is hence
approximated as a collection of truncated wedge (TW) cells. The trapezoidal sides of these wedges
are parallel to the
coordinate remains unaffected. Each torus cell is hence
approximated as a collection of truncated wedge (TW) cells. The trapezoidal sides of these wedges
are parallel to the ![]() plane and the rectangular sides are perpendicular to this plane.
Since all TW cells have exactly the same size and shape when coming from the same torus cell, it
suffices to concentrate on just one of them. These representative TW cells will be placed inside the
plane and the rectangular sides are perpendicular to this plane.
Since all TW cells have exactly the same size and shape when coming from the same torus cell, it
suffices to concentrate on just one of them. These representative TW cells will be placed inside the
![]() plane, such that the positive
plane, such that the positive ![]() axis divides the trapezoidal sides into two equal areas.
The collection of all representative TW cells has the shape of a wedge with opening angle
axis divides the trapezoidal sides into two equal areas.
The collection of all representative TW cells has the shape of a wedge with opening angle ![]() .
.
![]() (the treatment of the lens ellipse is analogous) in 3D
in implicit form (see Figure 18.6):
(the treatment of the lens ellipse is analogous) in 3D
in implicit form (see Figure 18.6):
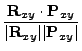
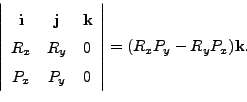
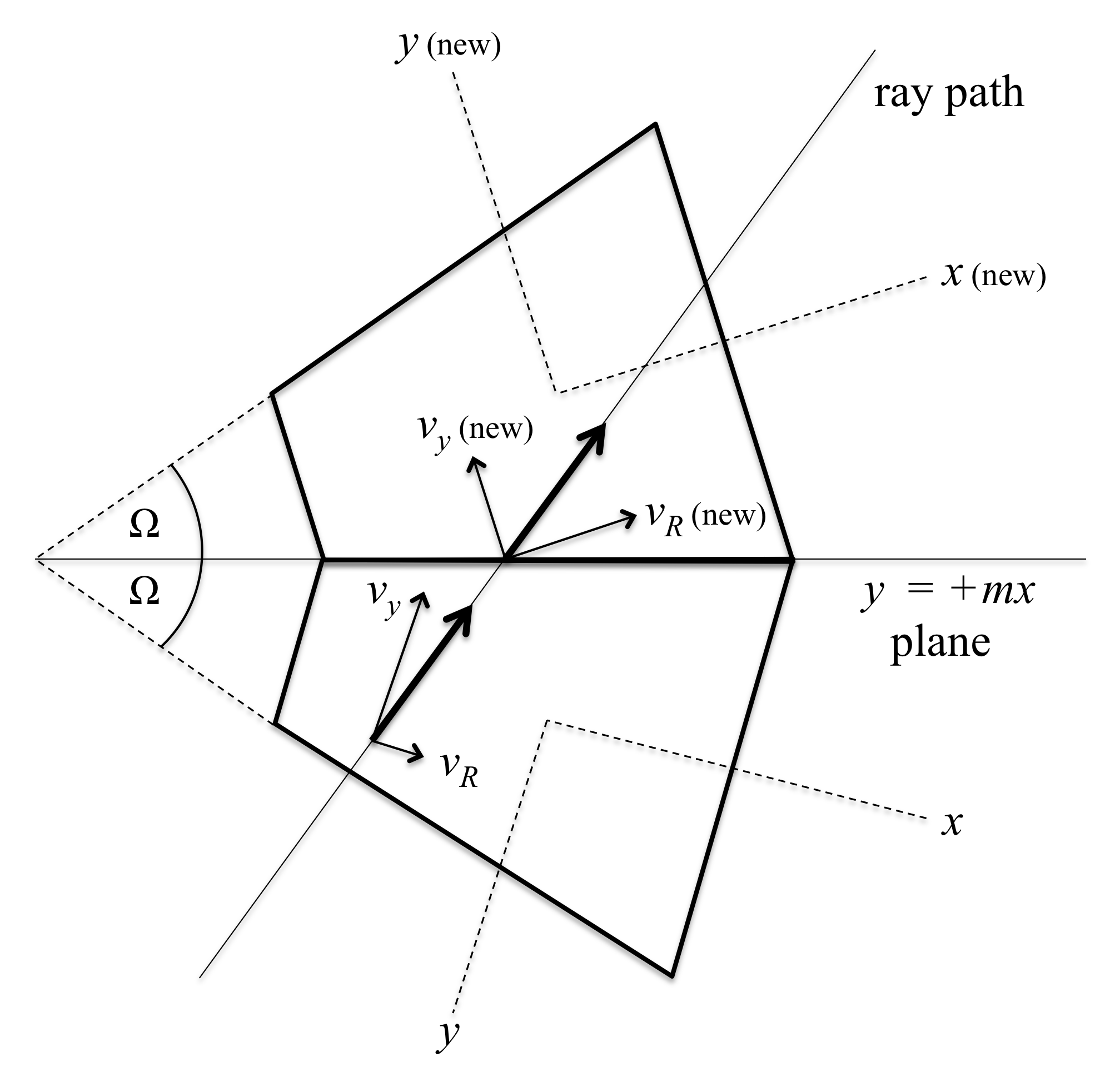
![]() in 3D cylindrical coordinates
in 3D cylindrical coordinates
![]() in terms of their
rotating unit vectors
in terms of their
rotating unit vectors
![]() , the ray equation of motion
in Eq.(18.36) and the definition of the gradient operator in 3D
cylindrical coordinates:
, the ray equation of motion
in Eq.(18.36) and the definition of the gradient operator in 3D
cylindrical coordinates:
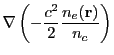
![]() and velocity
and velocity ![]() is
computationally somewhat inconvenient, we will transform these to the tangential
acceleration
is
computationally somewhat inconvenient, we will transform these to the tangential
acceleration
![]() and velocity
and velocity ![]() by using:
by using:
![]() (excluding zero) obtained from solving all six (two for each
kind of cell wall) polynomials in Eqs.(18.184-18.186) as
(excluding zero) obtained from solving all six (two for each
kind of cell wall) polynomials in Eqs.(18.184-18.186) as
![]() . Using
. Using
![]() to obtain new positions via
Eqs.(18.172-18.174) guarantees that we stay inside the cell, but using it
to determine the intermediate state via Eqs.(18.178-18.180) might
take us outside of the cell, i.e.
to obtain new positions via
Eqs.(18.172-18.174) guarantees that we stay inside the cell, but using it
to determine the intermediate state via Eqs.(18.178-18.180) might
take us outside of the cell, i.e.
![]() cell. To enforce the
intermediate state inside the cell, we determine also the minimum
cell. To enforce the
intermediate state inside the cell, we determine also the minimum
![]() (excluding zero)
obtained from solving all six (two for each kind of cell wall) linear intermediate state equations
in Eqs.(18.178-18.180) by replacing
(excluding zero)
obtained from solving all six (two for each kind of cell wall) linear intermediate state equations
in Eqs.(18.178-18.180) by replacing
![]() by the
corresponding cell wall values. Denoting this minimum intermediate state
linear time as
by the
corresponding cell wall values. Denoting this minimum intermediate state
linear time as
![]() , we form the allowed stepping time
, we form the allowed stepping time
![]() inside the
cell as:
inside the
cell as:
![]() need a special treatment, as 3D cylindrical blocks
touching the axis have no meaningful neighbor block information. To outline the strategy, we
consider the 3D cylindrical axis to be hollow and to have a finite tiny radius
need a special treatment, as 3D cylindrical blocks
touching the axis have no meaningful neighbor block information. To outline the strategy, we
consider the 3D cylindrical axis to be hollow and to have a finite tiny radius ![]() with no radial, angular
and axial acceleration terms (
with no radial, angular
and axial acceleration terms (
![]() ). Figure 18.13
shows a ray crossing the hollow axis.
). Figure 18.13
shows a ray crossing the hollow axis.
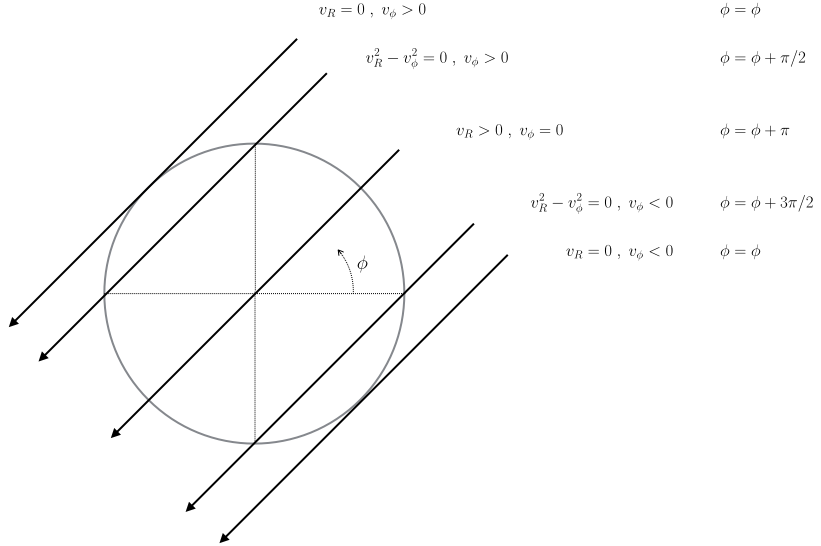
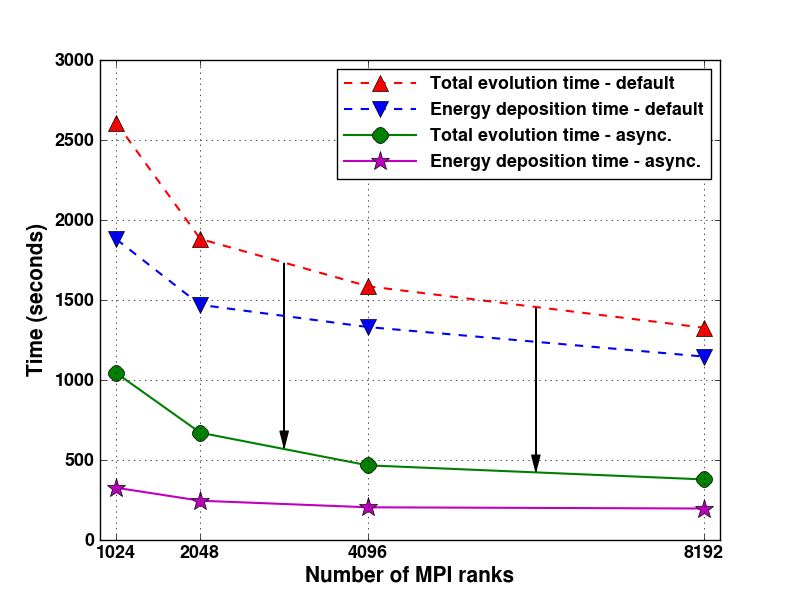
![$\displaystyle \max \left[ \mathrm{int} \left( \frac{N_\mathrm{rays}}{\mathrm{ed\_laserIOMaxNumberOfRays}} \right), 1 \right],$](img1702.png)
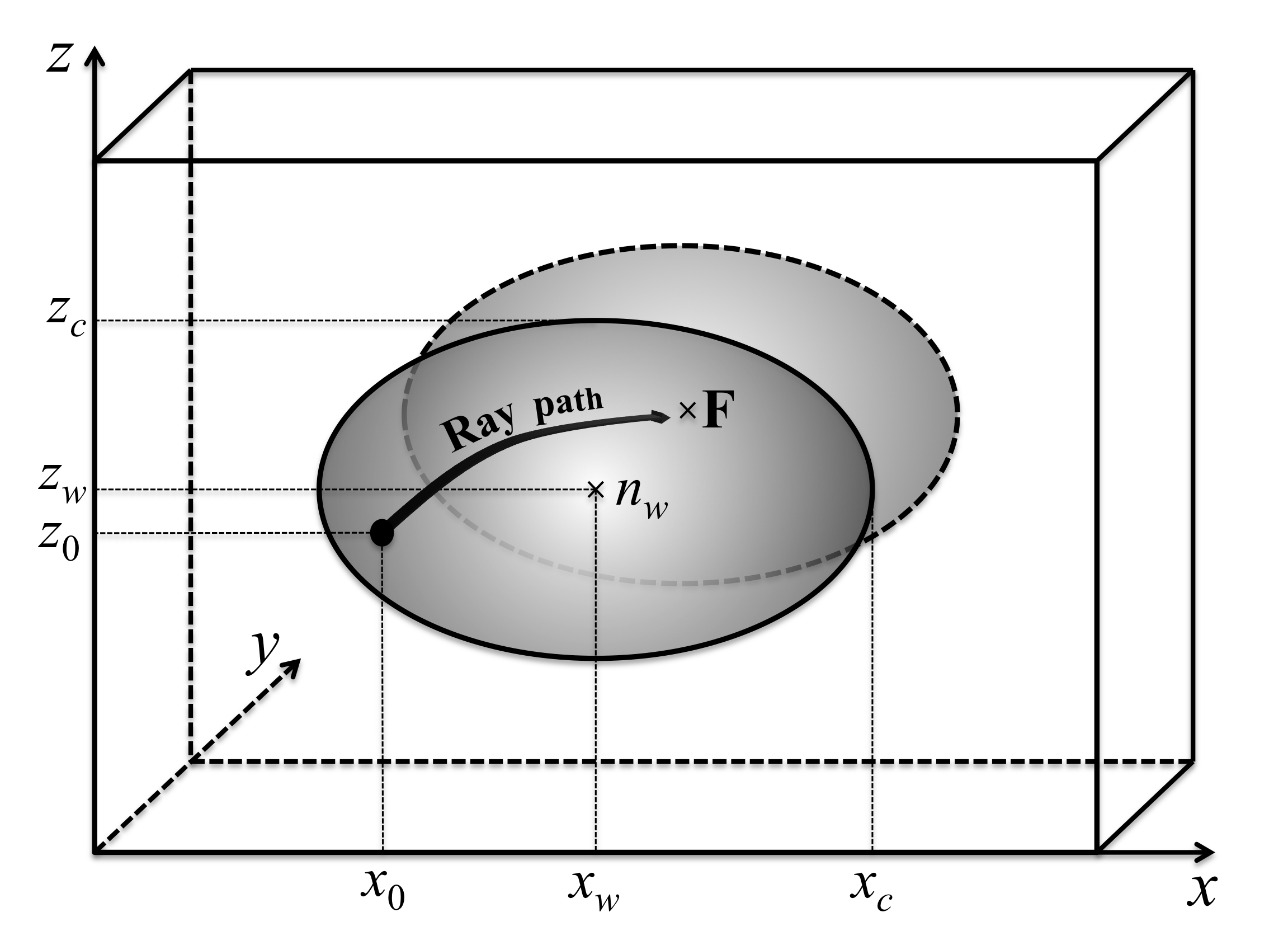
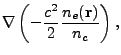
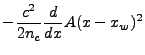
![]() and
and ![]() will be different. What this means is that the ray will not
hit the focal point. For that to occur, both times must be equal, hence we must have
will be different. What this means is that the ray will not
hit the focal point. For that to occur, both times must be equal, hence we must have
![$\displaystyle \frac{4}{3} \left (\frac{2 \pi}{m_e} \right)^{1/2} \frac{e^4}{n_c...
...{Z[{\bf r}(t)]n_e[{\bf r}(t)]^2\ln \Lambda[{\bf r}(t)]}{T_e[{\bf r}(t)]^{3/2}}.$](img1772.png)
![$\displaystyle \frac{4}{3} \left (\frac{2 \pi}{m_e} \right)^{1/2}
\frac{n_we^4}{n_ck^{3/2}{T_w}^{3/2}}n_e[{\bf r}(t)]$](img1776.png)
![$\displaystyle \nu_{ib,w} \frac{n_e[{\bf r}(t)]}{n_w},$](img1777.png)
![$\displaystyle \int_0^{t_{cross}}\nu_{ib}[{\bf r}(t)] dt$](img1780.png)
![$\displaystyle \frac{\nu_{ib,w}}{n_w}\int_0^{t_{cross}}n_e[{\bf r}(t)] dt$](img1781.png)
![$\displaystyle \frac{\nu_{ib,w}}{n_w}\int_0^{t_{cross}} n_w + A(x[t]-x_w)^2 + B(z[t]-z_w)^2 dt.$](img1782.png)
![$\displaystyle \int_0^{t_{cross}} (x[t]-x_w)^2 dt$](img1783.png)
![$\displaystyle \int_0^{t_{cross}}
\left[(x_0-x_w)\cos (\sqrt{k} t) + \frac{v_x}{\sqrt{k}} \sin (\sqrt{k} t) \right]^2 dt$](img1784.png)
![$\displaystyle \int_0^{t_{cross}}\nu_{ib}[{\bf r}(t)] dt$](img1780.png)
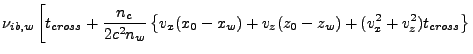
![$\displaystyle \left.+\frac{n_c-n_w}{2n_w}
\left\{\frac{(x_0-x_w)^2}{(x_c-x_w)^2}+\frac{(z_0-z_w)^2}{(z_c-z_w)^2}\right\}t_{cross}\right].$](img1789.png)
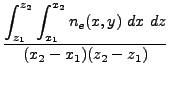
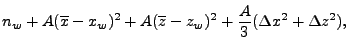
![$\displaystyle T_w\left[\dfrac{\langle n_e \rangle}{n_w}\right]^{2/3}.$](img1823.png)
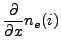
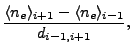
![$\displaystyle {\overline P} \frac{w_{ray}}{\sum w_{ray}}
\exp \left\{ - \nu_{ib,w} t_{cross}\left[1+\frac{AR_{ray}}{2n_w}\right] \right\},$](img1884.png)
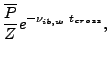
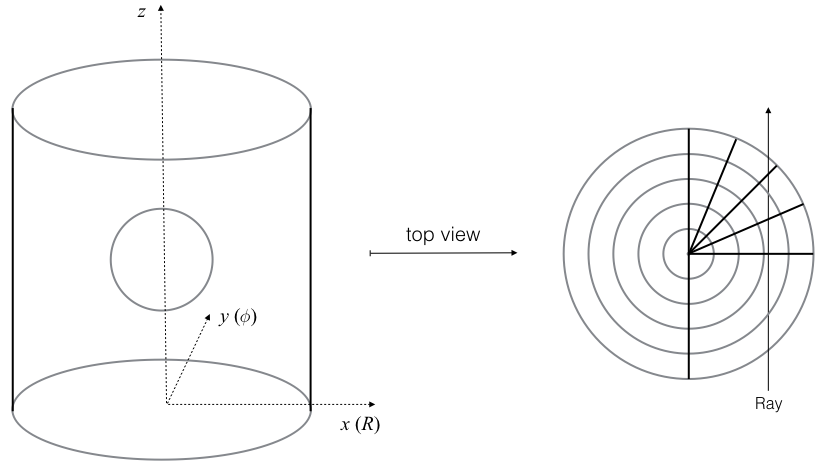
![]() cm,
cm,
![]() cm and
cm and
![]() cm. The laser ring consists
of
cm. The laser ring consists
of ![]() rays, has a radius of
rays, has a radius of ![]() cm and is shot along the 3D cartesian
cm and is shot along the 3D cartesian ![]() direction
on the mantle center at
direction
on the mantle center at ![]() cm. Each ray carries a power of 1 erg/s. A uniform electron
number density (half the critical density) is set throughout the can to ensure no radial
and angular acceleration. Speed adjustment of the rays as they enter the domain is supressed,
hence all rays will travel with the speed of light
cm. Each ray carries a power of 1 erg/s. A uniform electron
number density (half the critical density) is set throughout the can to ensure no radial
and angular acceleration. Speed adjustment of the rays as they enter the domain is supressed,
hence all rays will travel with the speed of light ![]() through the can. A uniform inverse
Bremsstrahlungsrate of
through the can. A uniform inverse
Bremsstrahlungsrate of
![]() process, we resort to a simpler
method. We define an angular tic
process, we resort to a simpler
method. We define an angular tic
![]() value as the minimum angular separation of each
ray in the beam:
value as the minimum angular separation of each
ray in the beam:
![]() and expands
afterwards regaining its original shape. On exit the laser ring should have the same
radius as on entry and all rays should have the same initial speed, which increases
towards the singular point when the ring contracts and decreases afterwards when the
ring expands. Inside the can the laser ring traces an hourglass shape with a single
point at its center.
and expands
afterwards regaining its original shape. On exit the laser ring should have the same
radius as on entry and all rays should have the same initial speed, which increases
towards the singular point when the ring contracts and decreases afterwards when the
ring expands. Inside the can the laser ring traces an hourglass shape with a single
point at its center.
![]() cm,
cm,
![]() cm and
cm and
![]() cm. The laser ring consists
of
cm. The laser ring consists
of ![]() rays, has a radius of
rays, has a radius of ![]() cm and is shot along the 3D cartesian
cm and is shot along the 3D cartesian ![]() direction
on the lid center at
direction
on the lid center at ![]() cm. Each ray carries a power of 1 erg/s. A linear electron
number density gradient
cm. Each ray carries a power of 1 erg/s. A linear electron
number density gradient