Next: 18.7 Turbulence Measurement Up: 18. Local Source Terms Previous: 18.5 Heatexchange Contents Index
The Flame unit implements an artificial reaction front model based on a simplified single-variable reaction-diffusion model. This is intended to be used to model the behavior of under-resolved reaction fronts propagated spatially by thermal diffusion, commonly called flames or deflagration fronts. As the reaction-diffusion front is also carried with the fluid, this model is sometimes termed an advection-diffusion-reaction (ADR) model. The principal usage to date of this model has been during the deflagration phase of models of Type Ia Supernovae. See Townsley et al. (2007), from which some text in this section has been adapted, and works that reference it for examples.
Generally, an ADR scheme characterizes the location of a flame front using a reaction
progress variable, ![]() , which increases monotonically across the front
from 0 (fuel) to 1 (ash).
Evolution of this progress variable is accomplished via an
advection-diffusion-reaction equation of the form
, which increases monotonically across the front
from 0 (fuel) to 1 (ash).
Evolution of this progress variable is accomplished via an
advection-diffusion-reaction equation of the form
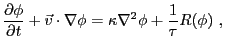 |
(18.276) |
| (18.277) |
The KPP reaction term, however, has two serious drawbacks. Formally, the
flame speed is only single valued for initial conditions that are precisely
zero (and stay that way) outside the burned region
(Xin 2000), which cannot really be effected in a hydrodynamics simulation.
This can lead to an unbounded increase of the propagation speed, which is
precisely the property we wish to have under good control. Secondly, the
progress variable ![]() takes an infinite amount of time to actually reach
1 (complete consumption of fuel). While not a fatal flaw like the flame speed
problem, this is a problem
for our simulations in which we would like to have a localized flame front so
that fully-burned ash can be treated as pure NSE material.
takes an infinite amount of time to actually reach
1 (complete consumption of fuel). While not a fatal flaw like the flame speed
problem, this is a problem
for our simulations in which we would like to have a localized flame front so
that fully-burned ash can be treated as pure NSE material.
Both of these drawbacks can be ameliorated by a slight modification of the reaction term (S. Asida, private communication) to
Diffusive flames are known to be subject to a curvature effect that affects the flame speed when the radius of curvature is similar to the flame thickness, a frequent circumstance with modestly-resolved flame front structure. In testing, the curvature effect of the step-function reaction rate proved surprisingly strong, likely due to the exponential “nose” that the flame front possesses (Vladimirova et al. 2006). Both KPP and sKPP show significantly better curvature properties.
The unit is divided into several subunits to allow flexibility in how the propagation speed is determined and how the enery release of the reaction front takes place. The main subunit FlameMain just implements the actual the reaction and diffusion terms defined above. There is currently only one implementation, RDSplit5point, that uses operator-split steps for the reaction and diffusion, and a 5 point stencil for the Laplacian operator.
The order of operations occurs as follows, for each block of the mesh in
sequence: The progress variable, ![]() , stored in FLAM_MSCALAR is
extracted, the Unit-internal function fl_flameSpeed() is called to
fill a temporary array with the flame speed evaluated for each cell in the
current block. The mesh scalar FLAM_MSCALAR is then updated based on
this flame speed while saving temporarily the effective
, stored in FLAM_MSCALAR is
extracted, the Unit-internal function fl_flameSpeed() is called to
fill a temporary array with the flame speed evaluated for each cell in the
current block. The mesh scalar FLAM_MSCALAR is then updated based on
this flame speed while saving temporarily the effective ![]() for this
time step. This information is then passed on to the internal function
fl_effects() which performs any energy release or other desired side
effects of the propagation of the RD front. Note both the temporary arrays
storing the flame speed and the
for this
time step. This information is then passed on to the internal function
fl_effects() which performs any energy release or other desired side
effects of the propagation of the RD front. Note both the temporary arrays
storing the flame speed and the ![]() for the current block are
destroyed before processing the next block. However some implementations of
fl_flameSpeed() may save this information in the main grid arrays for
informational or other purposes.
for the current block are
destroyed before processing the next block. However some implementations of
fl_flameSpeed() may save this information in the main grid arrays for
informational or other purposes.
The flame speed is generally determined by various physical quantities on the grid. However, since the flame is generally an artificial reaction front, many aspects other than the composition may influence the speed. The simplest alternative implementation for determining the flame speed, which is the default one, is Flame/FlameSpeed/Constant. This simply sets a constant flame speed everywhere on the grid.
The flame speed can also include a turbulence-flame interaction (TFI). The implemented options are discussed in Jackson, Townsley, & Calder (2014, submitted). This is accomplished by including one of the implementations under, for example Flame/FlameSpeed/Constant/TFI. Since the TFI always modifies some base flame speed, it is generally included as a implementation of that type of flame speed, in this case a constant flame speed. In order to facilitate sharing of the TFI components, they are stored in their own implementation directories under Flame/FlameSpeed/turbulent and included as needed. All of the TFI options require the inclusion of the Turb unit which provides a measurement of the local turbulence strength.
The flame effects subunit performs functions related to the actual energy
deposition or changes in abundances caused by advance of the reaction front
being modeled by the reaction-diffusion progress variable ![]() . The
simplest implementation, included under Flame/FlameEffects/EIP,
implements fixed energy input and change in
. The
simplest implementation, included under Flame/FlameEffects/EIP,
implements fixed energy input and change in ![]() and
and ![]() across the
reaction front. This is constructed to utilize the fully ionized
electron-ion plasma EOS called the "Helmholtz" EOS in Flash.
across the
reaction front. This is constructed to utilize the fully ionized
electron-ion plasma EOS called the "Helmholtz" EOS in Flash.