Subsections
FLASH has the ability to simulate plasmas which have separate ion,
electron, and radiation temperatures (see Chp:HEDP). Usually,
simulations which multiple temperatures have several physics models
active including:
- Electron thermal conduction
- Ion/Electron equilibration
- Radiation emission, absorption, and diffusion
This section contains a series of simulations which verify FLASH
through comparisons with analytic solutions of steady shocks where
various assumptions are active. Unfortunately, no single analytic
solution contains three distinct temperatures with realistic physical
coefficients. Thus, each simulation is performed with a different set
of assumptions active. Taken together, they adequately exercise the 3T
capabilities in FLASH.
35.8.1 Shafranov Shock
The Shafranov problem (Shafranov, 1957) is a one-dimensional problem
that provides a good verification for structure of 1D shock waves in a
two-temperature plasma with separate ion and electron
temperatures. The Shafranov shock solutions takes as input a given
upstream condition and shock speed. It then computes the downstream
conditions and a shock profile. The solution is fairly sophisticated
in that it takes into account electron thermal conduction and
ion/electron equilibration. An assumption is made that the electron
entropy is continuous across the shock. Thus, immediately downstream
of the shock, the ion-temperature is substantially higher than the
electron temperature. Far downstream, the temperature
equilibrate. Electron conduction creates a preheat region upstream of
the shock. An gamma-law EOS is used (typically with
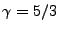 ).
).
Unfortunately, the Shafranov shock solution can only be simplified to
an ODE which must be numerically integrated. The ShafranovShock
simulation directory includes analytic solutions for several materials
including Hydrogen, Helium, and Xenon in the files
plasma_shock.out, plasma_shock_Z2.out, and
plasma_shock_Z54.out respectively.
Several solutions are compared here for the fully-ionized Helium case
with the following initial/boundary conditions:
- Upstream Ion/Electron Temperature: 5 eV
- Upstream Density: 0.0018 g/cc
- Upstream Velocity: 0.0 cm/s
- Shock Speed: 1.623415272E+07 cm/s
Figure 35.82, Figure 35.83, and
Figure 35.84, shows the electron/ion temperature,
density, and velocity at 0.15 ns for three cases:
- Analytic Solution: This is the analytic solution for the
steady shock. This solution is used to initialize the FLASH
simulations. The simulations are correct to the extent that they
are able to maintain this shock profile.
- Entropy Advection Solution: This is a 1D FLASH simulation
using the split hydrodynamics solver in “entropy advection” mode
as described in Sec:3TEntropyAdvection.
- RAGE-like Solution: This is a 1D FLASH simulation using the
split hydrodynamics solver in “RAGE-like” mode as described in
Sec:3TRageLikeHydro.
The figures show that the both the entropy advection and RAGE-like
FLASH simulation are able to maintain the correct shock
speeds. However, the entropy advection approach closely matches the
correct analytic ion temperature profile while the RAGE-like
simulation a peak ion temperature that is too low. This is the
expected behavior since the RAGE-like mode does not attempt to ensure
that electrons are adiabatically compressed by the shock.
This simulation can be setup with the following setup command:
# For the Entropy Advection Case:
./setup ShafranovShock -auto -1d +pm4dev +3t -parfile=flash_Z2.par
# For the RAGE-like Case:
./setup ShafranovShock -auto -1d +pm4dev +3t -parfile=ragelike_Z2.par
Figure 35.82:
Electron and ion temperatures from
Shafranov shock simulation
|
|
Figure 35.83:
Mass density from Shafranov shock
simulation
|
|
Figure 35.84:
Velocity from Shafranov shock
simulation
|
|
35.8.2 Non-Equilibrium Radiative Shock
The non-equilibrium radiative shock solution is an analytical solution
to a steady, 1D, radiative shock where 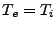 but
but
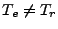 . It is presented in (Lowrie, 2008). A constant opacity is
assumed, making this a gray simulation. The “analytic”
solution is fairly complex and reduces to an ODE which must be
evaluated numerically. This ODE is evaluated for a given set of
upstream conditions and a given Mach number (evaluated relative to the
upstream sound speed). A gamma-law equation of state is assumed.
. It is presented in (Lowrie, 2008). A constant opacity is
assumed, making this a gray simulation. The “analytic”
solution is fairly complex and reduces to an ODE which must be
evaluated numerically. This ODE is evaluated for a given set of
upstream conditions and a given Mach number (evaluated relative to the
upstream sound speed). A gamma-law equation of state is assumed.
The FLASH implementation of this simulation resides in the
GrayDiffRadShock simulation directory. The simulation can be
set up using the following command:
./setup -auto GrayDiffRadShock -1d +pm4dev +splitHydro +3t mgd_meshgroups=1
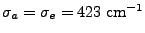 and
and
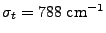 (see Sec:OpacityConstant). A
(see Sec:OpacityConstant). A
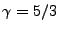 gamma-law EOS is used with
gamma-law EOS is used with 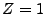 and
and 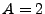 . The electron and
ion temperatures are forced to equilibrium by using the Spitzer
Heatexchange implementation (see:
Sec:HeatexchangeSpitzer) where the ion/electron equilibration
time has been reduced by a factor of
. The electron and
ion temperatures are forced to equilibrium by using the Spitzer
Heatexchange implementation (see:
Sec:HeatexchangeSpitzer) where the ion/electron equilibration
time has been reduced by a factor of 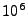 by setting the
hx_ieTimeCoef runtime parameter.
by setting the
hx_ieTimeCoef runtime parameter.
The initial conditions are defined by a step function where the jump
occurs at 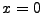 . The upstream (
. The upstream (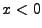 ) and downstream (
) and downstream (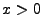 )
conditions are chosen so that the shock remains stationary. The
correct jump conditions are to maintain a stationary mach two shock
are:
)
conditions are chosen so that the shock remains stationary. The
correct jump conditions are to maintain a stationary mach two shock
are:
-
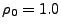 g/cc
g/cc
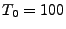 eV
eV
-
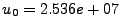 cm/s
cm/s
-
 g/cc
g/cc
-
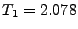 eV
eV
-
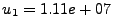 cm/s
cm/s
where the subscript 1 represents downstream conditions and the
subscript 0 represents upstream conditions. The runtime parameter
sim_P0 representing the ratio of radiation to matter pressure
is set to  .
.
The verification test is successful to the extent that FLASH is able
to maintain a stationary shock with the correct steady state spatial
profile as shown in Figure 8 of (Lowrie, 2008). This is an excellent
verification test in that no special modifications to the FLASH code
are needed to perform this test. The simulation is run for 4.25 ns
which is enough time for the initial step function profile to reach a
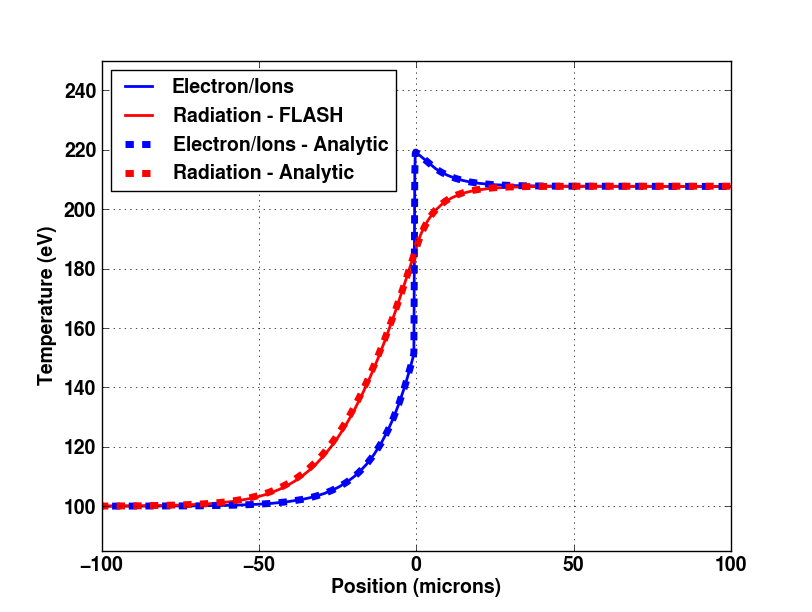
steady state solution. Figure 35.85 compares the
temperatures in the FLASH simulation to the analytic
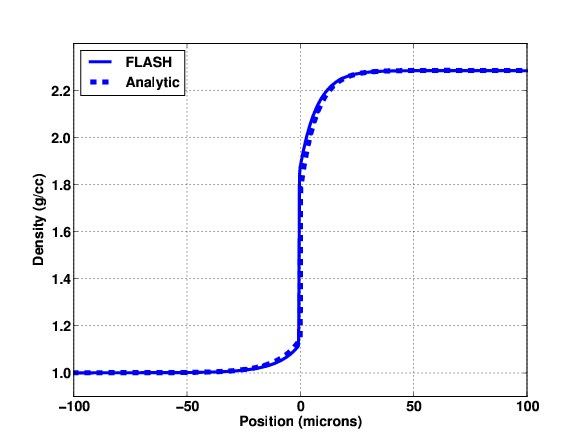
solution. Figure 35.86 compares density to the analytic
solution. Excellent agreement is obtained.
Figure 35.85:
Temperatures from non-equilibrium
radiative shock simulation. The FLASH results are compared to
analytic solution.
|
|
Figure 35.86:
Mass density from non-equilibrium
radiative shock simulation. The FLASH result is compared to the
analytic solution.
|
|
35.8.3 Blast Wave with Thermal Conduction
The ReinickeMeyer blast wave solution (Reinicke, 1991) models a blast wave
in a single temperature fluid with thermal conduction. The
semi-analytic solution reduces to an ODE which must be integrated
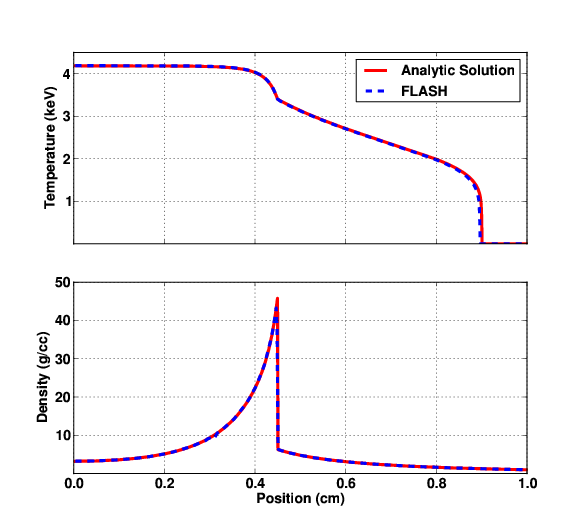
numerically. Figure 35.87 compares a FLASH simulation to
the analytic solution (obtained from cococubed.asu.edu/code_pages/vv.shtml after 0.3242 ns for a particular set of initial
conditions. Excellent agreement is obtained with the analytic
solution. The image shows that at this time the blast wave is at
approximately 0.45 cm and the conduction front is at 0.9 cm. The
simulation can be set up using the following command:
./setup -auto ReinickeMeyer -1d +pm4dev +spherical -parfile=flash_SPH1D.par
Figure 35.87:
Mass density and temperature from
ReinickeMeyer blast wave FLASH simulation compared to analytic solution.
|
|
![]() but
but
![]() . It is presented in (Lowrie, 2008). A constant opacity is
assumed, making this a gray simulation. The “analytic”
solution is fairly complex and reduces to an ODE which must be
evaluated numerically. This ODE is evaluated for a given set of
upstream conditions and a given Mach number (evaluated relative to the
upstream sound speed). A gamma-law equation of state is assumed.
. It is presented in (Lowrie, 2008). A constant opacity is
assumed, making this a gray simulation. The “analytic”
solution is fairly complex and reduces to an ODE which must be
evaluated numerically. This ODE is evaluated for a given set of
upstream conditions and a given Mach number (evaluated relative to the
upstream sound speed). A gamma-law equation of state is assumed.
![]() . The upstream (
. The upstream (![]() ) and downstream (
) and downstream (![]() )
conditions are chosen so that the shock remains stationary. The
correct jump conditions are to maintain a stationary mach two shock
are:
)
conditions are chosen so that the shock remains stationary. The
correct jump conditions are to maintain a stationary mach two shock
are: