14. 3T Capabilities for Simulation of HEDP Experiments

The FLASH code has been extended with numerous capabilities to allow it to simulate laser-driven High Energy Density Physics (HEDP) experiments. These experiments often require a multi-temperature treatment of the plasma where the ion temperature, $T_\mathrm{ion}$ and the electron temperature $T_\mathrm{ele}$ are not necessarily equal. Thermal radiation effects are also important in many High Energy Density (HED) plasmas. If the radiation field has a total energy density given by $u_\mathrm{rad}(\boldsymbol x, t)$ then the radiation temperature is defined as $T_\mathrm{rad} = (u_\mathrm{rad}/a)^{1/4}$ . The radiation field is not in equilibrium with the plasma and thus $T_\mathrm{rad} \ne T_\mathrm{ele} \ne T_\mathrm{ion}$ . We refer to this treatment, where these three temperatures are not necessarily equal, as a 3T treatment. This chapter is intended to describe the basic theory behind FLASH's 3T implementation to direct users to other parts of the manual and simulations which provide further details on how to use these new capabilities in FLASH.

The term “3T” is not meant to imply in any way that a gray treatment of the radiation field is being assumed. The radiation temperature is only used to represent the total energy density, which is integrated over all photon frequencies. The radiation temperature never directly enters the calculation. Thus, 3T refers to the fact that FLASH is being run in a mode where 3 independent components (ions, electrons, radiation) are being modeled. The radiation field is usually treated in a frequency dependent way through multigroup radiation diffusion as described below and in chp:RadTrans.

The equations which FLASH solves to describe the evolution of an unmagnetized 3T plasma are:

$\begin{subequations}\begin{gather}\frac{\partial \rho}{\partial t} + \nabla \cdo... ...t] = Q_\mathrm{las} - \nabla \cdot \boldsymbol q, \end{gather}\end{subequations}$

where:

$\rho$ is the total mass density
$\boldsymbol v$ is the average fluid velocity
$P_\mathrm{tot}$ is the total pressure defined as the sum over the ion, electron, and radiation pressures:

$\displaystyle P_\mathrm{tot} = P_\mathrm{ion} + P_\mathrm{ele} + P_\mathrm{rad}$ (14.2)
$E_\mathrm{tot}$ is the total specific energy which includes the specific internal energies of the electrons, ions, and radiation field along with the specific kinetic energy. Thus:

$\displaystyle E_\mathrm{tot} = e_\mathrm{ion} + e_\mathrm{ele} + e_\mathrm{rad} + \frac{1}{2} \boldsymbol v \cdot \boldsymbol v$ (14.3)
$\boldsymbol q$ is the total heat flux which is assumed to have a radiation and electron conductivity component:

$\displaystyle \boldsymbol q = \boldsymbol q_\mathrm{ele} + \boldsymbol q_\mathrm{rad}$ (14.4)
$Q_\mathrm{las}$ represents the energy source due to laser heating

Since the plasma is not assumed to have a single temperature, additional equations must be evolved to describe the change in specific internal energies of the ions, electrons, and radiation field. For the electrons and ions these equations are:

$\begin{subequations}\begin{gather}\frac{\partial}{\partial t}(\rho e_\mathrm{ion... ..._\mathrm{rad} - Q_\mathrm{abs} + Q_\mathrm{emis}, \end{gather}\end{subequations}$

where:

$c_{v,\mathrm{ele}}$ is the electron specific heat
$\tau_{ei}$ is the ion/electron equilibration time
$Q_\mathrm{abs}$ represents the increase in electron internal energy due to the total absorption of radiation
$Q_\mathrm{emis}$ represents the decrease in electron internal energy due to the total emission of radiation

The 3T equation of state in FLASH connects the internal energies, temperatures, and pressures of the components. Many different equations of state options exist in FLASH. These are described in Sec:3TEos. A full-physics HEDP simulation using FLASH will solve equations (Eqn:3TFull) and (Eqn:3TSpecies) using the 3T equation of state. These equations are somewhat redundant since (Eqn:3TFullEnergy) can be written as a sum of the other equations. These equations are also not yet complete, since it has not been described how many of the terms above are defined and computed in FLASH. The remainder of this chapter will describe this and direct readers to the appropriate sections of the manual where examples and further information can be found.

A series of operator splits is used to solve (Eqn:3TFull) and (Eqn:3TSpecies) in FLASH. First, all of the terms on the left hand sides of these equations are split off and solved in various code units. The remaining equations:

$\begin{subequations}\begin{gather}\frac{\partial \rho}{\partial t} + \nabla \cdo... ... + P_\mathrm{rad} \nabla \cdot \boldsymbol v = 0, \end{gather}\end{subequations}$

describe the advection of conserved quantities and the effect of work. (Eqn:3THydroOnly) is solved by the Hydro unit. Chp:Hydrodynamics Unit describes the hydrodynamics solvers in a general way where only equations for conservation of total mass, momentum, and energy are considered. The extension of the FLASH hydrodynamics solvers to 3T is described in Sec:3THydro. Note that these equations are not in a conservative form because of the presence of the work terms in (Eqn:3THydroOnlyIon), (Eqn:3THydroOnlyEle), and (Eqn:3THydroOnlyRad). These work terms are divergent at shocks and cannot be directly evaluated. Two techniques are described in Sec:3THydro for coping with this issue.

The electron, ion, and radiation internal energy equations in the absence of the hydrodynamic terms are shown in (Eqn:3TNoHydro). The density is updated in the hydrodynamic update so for the remaining equations the density is assumed to be constant, and we remove the density from the time derivatives.

$\begin{subequations}\begin{gather}\rho \frac{\partial e_\mathrm{ion}}{\partial t... ..._\mathrm{rad} - Q_\mathrm{abs} + Q_\mathrm{emis}. \end{gather}\end{subequations}$

The first term on the right hand side of (Eqn:3TNoHydroIon) and (Eqn:3TNoHydroEle) describes the exchange of internal energy between ions and electrons through collisions. This term will force the ion and electron temperatures to equilibrate over time. The Heatexchange unit, described in Sec:HeatexchangeSpitzer, solves for this part of (Eqn:3TNoHydro). Specifically, it updates the ion and electron temperatures according to:

$\begin{subequations}\begin{gather}\frac{\partial e_\mathrm{ion}}{\partial t} = \... ...}}}{\tau_{ei}} (T_\mathrm{ion} - T_\mathrm{ele}). \end{gather}\end{subequations}$

The electron specific heat, $c_{v,\mathrm{ele}}$ is computed through calls to the equation of state. The ion/electron equilibration time is computed in the Heatexchange unit.

The second term on the right hand side of (Eqn:3TNoHydroEle) represents the transport of energy through electron thermal conduction. Thus the heat flux is defined as:

$\displaystyle \boldsymbol q_\mathrm{ele} = -K_\mathrm{ele} \nabla T_\mathrm{ele},$

(14.9)

where $K_\mathrm{ele}$ is the electron thermal conductivity and is computed in the Conductivity unit (see Sec:conductivity). The Diffuse unit, described in Chp:diffuse, is responsible for including the effect of conduction in FLASH simulations. Again, using operator splitting, the Diffuse unit solves the following equation over a time step:

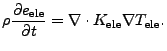$\displaystyle \rho \frac{\partial e_\mathrm{ele}}{\partial t} = \nabla \cdot K_\mathrm{ele} \nabla T_\mathrm{ele}.$

(14.10)

This equation can be solved implicitly over the time step to avoid time-step constraints. The electron conductivity is evaluated using a flux limiter to give more a physically realistic heat flux in regions where the electron temperature gradient is very large.

The remaining terms describe radiation transport. FLASH incorporates radiation effects using multigroup diffusion (MGD) theory. The total radiation flux, emission, and absorption terms which appear in (Eqn:3TNoHydro) contain contributions from each energy group. For group , where $1 \le g \le N_g$ , the total quantities can be written as summations over each group:

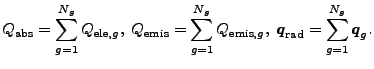$\displaystyle Q_\mathrm{abs} = \sum_{g=1}^{N_g} Q_{\mathrm{ele},g},\; Q_\mathrm... ...thrm{emis},g},\; \boldsymbol q_\mathrm{rad} = \sum_{g=1}^{N_g} \boldsymbol q_g.$

(14.11)

The change in the radiation energy density for each group,

, is described by:

$\displaystyle \frac{\partial u_g}{\partial t} + \nabla \cdot (u_g \boldsymbol v... ...ol v = -\nabla \cdot \boldsymbol q_g + Q_{\mathrm{emis},g} - Q_{\mathrm{abs},g}$

(14.12)

The total specific radiation energy is related to

through:

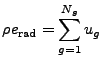$\displaystyle \rho e_\mathrm{rad} = \sum_{g=1}^{N_g} u_g$

(14.13)

The RadTrans unit is responsible for solving the radiation diffusion equations for each energy group. The RadTrans unit solves these diffusion equations implicitly by using the Diffuse unit. While the work term for the total radiation energy is computed in the Hydro unit, the distribution of that work amongst each energy group is performed in the RadTrans unit. chp:RadTrans describes in detail how the multigroup radiation diffusion package in FLASH functions. The group radiation flux, emission, and absorption terms are all defined in that chapter. These terms are functions of the material opacity which is computed by the Opacity unit and is described in Sec:Opacity.

The only remaining term in (Eqn:3TNoHydro) is $Q_\mathrm{las}$ which represents the deposition of energy by lasers into the electrons. The Laser implementation in the EnergyDeposition unit is responsible for computing $Q_\mathrm{las}$ . The geometrics optics approximation to laser energy deposition is used in FLASH. Sec:EnergyDeposition describes the theory and usage of the laser ray-tracing model in FLASH in detail.

As has been described above, the HEDP capabilities in FLASH are divided amongst many units including:

Hydro: Responsible for the 3T hydrodynamic update
Eos: Computes 3T equation of state
Heatexchange: Implements ion/electron equilibration
Diffuse: Responsible for implementing implicit diffusion solvers and computes effect of electron conduction
RadTrans: Implements multigroup radiation diffusion
Opacity: Computes opacities for radiation diffusion
Conductivity: Computes electron thermal conductivities
EnergyDeposition: Computes the laser energy deposition

Several simulations are included with FLASH which demonstrate the usage of the HEDP capabilities and, taken together, exercise all of the units listed above. These simulations are described briefly below. Sec:The supplied problems describes all of the simulations in detail. Below, the relevant simulations listed with brief descriptions.

MGDInfinite simulation, described in Sec:SimInfMedium: Simple 0D test of the exchange of energy between electrons, ions, and the radiation field
MGDStep simulation, described in Sec:SimMGDStep: Simple 1D test of electron conduction, ion/electron equilibration, and MGD
ShafranovShock simulation, described in Sec:SimShafShock: Simple 1D verification test of the structure of a shock in a radiationless plasma with $T_\mathrm{ele} \ne T_\mathrm{ion}$ .
GrayDiffRadShock simulation, described in Sec:SimGrayDiffRadShock: Simple 1D verification test of the structure of a radiating shock
ReinickeMeyer simulation, described in Sec:SimReinickeMeyer: Verification test of a spherical blast wave with thermal conduction
LaserSlab simulation, described in Sec:LaserSlab: Full physics 2D simulation which includes 3T hydrodynamics, tabulated EOS and opacity, MGD, electron conduction, and laser ray-tracing. This simulation is meant to demonstrate how to set up a complex simulation of an HEDP experiment