Next: 15.4 Radiation-Flux-Limiter Aware Hydrodynamics Up: 15. Hydrodynamics Units Previous: 15.2 Relativistic hydrodynamics (RHD) Contents Index
The FLASH4 code includes two magnetohydrodynamic (MHD) units that represent
two different algorithms. The first is the eight-wave model (8Wave) by Powell
et al. (1999) that is already present in FLASH2. The second is
a newly implemented unsplit staggered mesh algorithm (USM or StaggeredMesh).
It should be noted that there are several major differences between
the two MHD units. The first difference is how each algorithm
enforces the solenoidal constraint of magnetic fields.
The eight-wave model basically uses the truncation-error method, which
effectively removes the effects of unphysical magnetic monopoles if
they are generated during simulations. It does not, however, completely
eliminate monopoles that are spurious in a strict physical law.
To improve such unphysical effects in simulations, the unsplit staggered mesh
algorithm uses the constrained transport method (Evans and Hawley, 1988) to
enforce divergence-free constraints of magnetic fields.
This method is shown to maintain magnitudes of
![]() substantially low, e.g., to the orders of
substantially low, e.g., to the orders of
![]() or below, in most simulations.
The second major difference is that the unsplit staggered mesh algorithm
uses a directionally unsplit scheme to evolve the MHD governing equations,
whereas the eight-wave method uses a directionally splitting method as in FLASH2.
In general, the splitting method is shown to be robust, relatively
straightforward to implement, and generally faster than the unsplit
method. The splitting method, however, does generally introduce splitting
errors when solving one-dimensional subproblems in each sweep direction
for multidimensional MHD equations.
This error gets introduced in simulations because
(i) the linearized Jacobian flux matrices do not commute
in most of the nonlinear multidimensional problems
(LeVeque, 1992; LeVeque, 1998), and
(ii) in MHD, dimensional-splitting based codes are not
able to evolve the normal (to the sweep direction) magnetic field
during each sweep direction (Gardiner and Stone, 2005).
or below, in most simulations.
The second major difference is that the unsplit staggered mesh algorithm
uses a directionally unsplit scheme to evolve the MHD governing equations,
whereas the eight-wave method uses a directionally splitting method as in FLASH2.
In general, the splitting method is shown to be robust, relatively
straightforward to implement, and generally faster than the unsplit
method. The splitting method, however, does generally introduce splitting
errors when solving one-dimensional subproblems in each sweep direction
for multidimensional MHD equations.
This error gets introduced in simulations because
(i) the linearized Jacobian flux matrices do not commute
in most of the nonlinear multidimensional problems
(LeVeque, 1992; LeVeque, 1998), and
(ii) in MHD, dimensional-splitting based codes are not
able to evolve the normal (to the sweep direction) magnetic field
during each sweep direction (Gardiner and Stone, 2005).
Note that the eight-wave solver uses the same directionally splitting driver unit Driver/DriverMain/split as the PPM and RHD units do, while the unsplit staggered mesh solver (StaggeredMesh) has its own independent unsplit driver unit Driver/DriverMain/unsplit.
Both MHD units solve the equations of compressible ideal and non-ideal magnetohydrodynamics
in one, two and three dimensions on a Cartesian system.
Written in non-dimensional (hence without ![]() or
or ![]() coefficients) conservation form, these equations are
coefficients) conservation form, these equations are
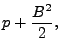 |
(15.23) | ||
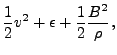 |
(15.24) | ||
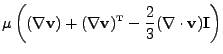 |
(15.25) |
The APIs of the MHD units are fairly minimal. The units honor all of hydrodynamics unit variables, interface functions and runtime parameters described in the above hydrodynamics unit chapter (see Chp:Hydrodynamics Unit). In addition, both the eight-wave and the unsplit staggered mesh units declare additional plasma variables and runtime parameters, which are listed in Table 15.7 and Table 15.8.
In the current release, the eight-wave unit serves as a default MHD solver. In order to choose the unsplit staggered mesh unit for MHD simulations, users need to include +usm in a setup script. The default eight-wave unit will be automatically chosen if there is no such specification included.
| Variable | Type | Description |
| magx | PER_VOLUME | |
| magy | PER_VOLUME | |
| magz | PER_VOLUME | |
| magp | (GENERIC) | magnetic pressure |
| divb | (GENERIC) | divergence of magnetic field |
| Variable | Type | Default | Description |
| UnitSystem | string | “none” | System of units in which MHD calculations are to be performed. Acceptable values are “none” “CGS” and “SI”. |
| killdivb | logical | .true. | Enable/disable divergence cleaning. |
| flux_correct | logical | .true. | Enable/disable flux correction on AMR grid. |
The overall procedure of the unsplit staggered mesh scheme can be broken up into the following steps (Lee, 2006; Lee and Deane, 2009; Lee, 2013):
Note that the procedure required in solving one-dimensional MHD equations is much
simpler than solving the multidimensional ones and only involves
the first through third and the fifth steps in the above oulined scheme.
The choices of TVD slope limiters available in the unsplit staggered mesh scheme (see
Table 15.9) includes the minmod
limiter as well as the compressible limiters
such as vanLeer or mc limiter. Another choice, called
hybrid limiter, can be used to provide a mixed type of limiters as described
in Balsara (2004). In this choice, one uses a compressible limiter
to produce a crisp representation for linearly
degenerate waves (e.g., an entropy wave and
left- and right-going Alfvén waves).
To this end, a compressible limiter can be applied
to the density and the magnetic fields variables,
where these variables contribute much of the
variations in such linearly degenerate waves.
Other variables, the velocity field
components and pressure, constitute four genuinely nonlinear
wave families (i.e., left- and right-going fast/slow magneto-sonic waves)
in MHD. These genuinely nonlinear wave families inherently
behave according to their self steepening mechanism and one
can simply use a diffusive but robust minmod limiter.
Another limiter, called limited, is also available (see details in
Toro, 1999, 2nd Ed., section 13.8.4), and users need to specify a runtime parameter
![]() (LimitedSlopeBeta in flash.par) if this limiter is chosen for a simulation.
(LimitedSlopeBeta in flash.par) if this limiter is chosen for a simulation.
The unsplit staggered mesh unit solves a set of discrete induction equations
in multi-dimensional problems to proceed
temporal evolutions of the staggered magnetic fields using electric
fields. For instance, in a two-dimensional staggered grid, the unsplit staggered mesh unit
solves a two-dimensional pair of discrete induction equations that were
found originally by Yee (1966):
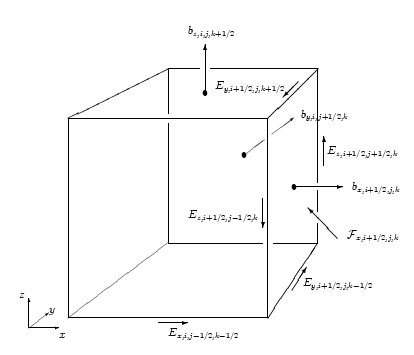
A three-dimensional schematic figure of the staggered grid geometry
with collocations of edge-based values (electric fields ![]() ) and
face based values (magnetic fields
) and
face based values (magnetic fields ![]() ) is shown
in Figure 15.2.
) is shown
in Figure 15.2.
One of the main advantages of using the CT-type of scheme is that
the cell face-centered magnetic fields
![]() and
and
![]() , which are updated via the above induction
equations, satisfy the divergence-free constraint locally.
The numerical divergence of the magnetic fields is defined as
, which are updated via the above induction
equations, satisfy the divergence-free constraint locally.
The numerical divergence of the magnetic fields is defined as
On an AMR grid, the unsplit staggered mesh scheme uses a direct injection method as a default to preserve divergence-free prolongation to the cell face-centered fields variables. This method is one of the simplest approaches that is offered by PARAMESH 4 to maintain the divergence-free constraint in prolongation. This simple method ensures the solenoidal constraint well enough where the fields are varying smoothly, but can introduce oscillations in regions of steep field gradient. In such cases Balsara's prolongation algorithm can be useful. Both prolongation algorithms are supported and enabled using runtime parameters in the unsplit staggered mesh solver (see Table 15.9 below).
To solve the above induction equations
(15.26) and (15.27) in a flux-CT
type scheme, it is required to construct cell edge-based electric fields.
The simplest choice is to use the cell face-centered high-order Godunov
fluxes and take an arithmetic average to construct cell-cornered
(edge-based in 3D) electric fields:
A high-order accurate version is also available by turning on
a logical switch E_modification in the unsplit staggered mesh scheme, which takes
Taylor series expansions of the cell-cornered electric field
![]() in all directions, followed by taking an arithmetic average of them (Lee, 2006; Lee and Deane, 2009).
in all directions, followed by taking an arithmetic average of them (Lee, 2006; Lee and Deane, 2009).
The last step in the unsplit staggered mesh scheme is to reconstruct the cell-centered magnetic fields
![]() and
and ![]() from the divergence-free face-centered magnetic fields.
The unsplit staggered mesh scheme takes arithmetic averages of the face-centered fields variables to obtain
the cell-centered magnetic fields, which is sufficient for second order accuracy.
After obtaining the new cell-centered magnetic fields, the total plasma energy
may need to be corrected in order to preserve the positivity of
the thermal temperature and pressure (Balsara and Spicer, 1999; Tóth, 2000).
This energy correction is very useful especially in problems involving very
low
from the divergence-free face-centered magnetic fields.
The unsplit staggered mesh scheme takes arithmetic averages of the face-centered fields variables to obtain
the cell-centered magnetic fields, which is sufficient for second order accuracy.
After obtaining the new cell-centered magnetic fields, the total plasma energy
may need to be corrected in order to preserve the positivity of
the thermal temperature and pressure (Balsara and Spicer, 1999; Tóth, 2000).
This energy correction is very useful especially in problems involving very
low ![]() plasma flows.
plasma flows.
There are several choices available for calculating high order Godunov fluxes in the unsplit staggered mesh scheme. The default solver is Roe's linearized approximate solver, which takes into account all seven waves that arise in the MHD equations. The Roe solver can adopt one of the two entropy fix routines (Harten, 1983; Harten and Hyman, 1983) in ordetblrefr to avoid unphysical states near strong rarefaction regions. As all seven waves are considered in Roe's solver, high numerical resolutions can be achieved in most cases. However, Roe's solver still can fail to maintain positive states near very low densities even with the entropy fix. In this case, computationally efficient and positively conservative Riemann solvers such as HLL (Einfeldt et al., 1991), HLLC (S. Li, 2005), or HLLD (Miyoshi and Kusano, 2005) can be used to maintain positive states in simulations. A hybrid type of Riemann solver which combines using the Roe solver for high accuracy and HLLD for stability is also available.
The USM solver has been recently extended also for 2D and 2.5D cylindrical (R-Z) geometries, both for uniform grids and AMR. In the cylindrical implementation, we followed the guidelines of Mignone et al. (2007) and Skinner & Ostriker (2010). Special care was also taken to ensure a divergence free interpolation of the staggered magnetic field components, when grid movements occur in AMR. This novel prolongation scheme is based on the methods described in Balsara (2001, 2004) and Li & Li (2004). More information regarding the cylindrical implementation can be found in Tzeferacos et al. (2012, in print) whereas new test problems, provided with this release, are available at Sections 35.2.3 and 35.2.4. Handling of different geometries will be available in future releases.
By the nature of very small numerical dissipations in PPM, unphysical
oscillations in discontinuous MHD solutions can appear
in a specific flow region, referred to as a slowly moving shock (SMS)
relative to the grid. This new approach handles numerical non-oscillatory MHD solutions using
PPM in SMS regions.
The SMS should not be confused with so-called ”slow MHD shock” which
corresponds to two slow waves (i.e., ![]() ) in MHD,
where
) in MHD,
where ![]() is the slow magneto-acoustic velocity.
is the slow magneto-acoustic velocity.
The method first detects a local, slowly moving shock, and considers an upwind direction to compute a monotonicity-preserving slope limiter. This new approach, in addition to improving the numerical solutions in MHD to levels that reduce (or eliminate) such oscillatory behaviors while preserving sharp discontinuities in MHD, is also simple to implement. The method has been verified against the results from other high-resolution shock-capturing (HRSC) methods such as MUSCL and WENO schemes.
In order to enable the SMS treatment for PPM, users set a runtime parameter upwindTVD=.true. in flash.par. The SMS method does require to have an extended stencil, and users should specify +supportPPMUpwind in setup. See more in Section 15.1.3.
|
| Variable | Type | Default | Description |
| killdivb | logical | .true. | On/off
|
| E_modification | logical | .true. | Enable/disable high-order electric field construction |
| E_upwind | logical | .false. | Enable/disable an upwind update for induction equations |
| energyFix | logical | .true. | Enable/disable energy correction |
| facevar2ndOrder | logical | .true. | Turn on/off a second-order facevar update |
| ForceHydroLimit | logical | .false. | On/off pure Hydro mode |
| prolMethod | string | "INJECTION_PROL" | Use either direct injection method ("INJECTION_PROL") or Balsara's method ("BALSARA_PROL") in prolonging divergence-free magnetic fields stored in face-centered variables |
| RiemannSolver | string | "ROE" | "HLLD" is additionally available for MHD, "Hybrid" is also available for MHD. |
After all sweeps are completed, the MHD unit enforces magnetic field divergence cleaning. In the current release only a diffusive divergence cleaning method (truncation-error method), which was the default method in FLASH2, is supported and the later release of the code will incorporate an elliptic projection cleaning method.
The ideal part of the MHD equations are solved using a high-resolution, finite-volume numerical scheme with MUSCL-type (van Leer, 1979) limited gradient reconstruction. In order to maximize the accuracy of the solver, the reconstruction procedure is applied to characteristic variables. Since this may cause certain variables, such as density and pressure, to fall outside of physically meaningful bounds, extra care is taken in the limiting step to prevent this from happening. All other variables are calculated in the unit from the interpolated characteristic variables.
In order to resolve discontinuous Riemann problems that occur at computational cell interfaces, the code by default employs a Roe-type solver derived in Powell et al. (1999). This solver provides full characteristic decomposition of the ideal MHD equations and is, therefore, particularly useful for plasma flow simulations that feature complex wave interaction patterns. An alternative Riemann solver of HLLE type, provided in FLASH2, has not been incorporated into FLASH4 yet.
Time integration in the MHD unit is done using a second-order, one-step method due to Hancock (Toro, 1999). For linear systems with unlimited gradient reconstruction, this method can be shown to coincide with the classic Lax-Wendroff scheme.
A difficulty particularly associated with solving the MHD equations
numerically lies in the solenoidality of the magnetic field. The
notorious
![]() condition, a strict physical law, is very hard
to satisfy in discrete computations. Being only an initial condition
of the MHD equations, it enters the equations indirectly and is not,
therefore, guaranteed to be generally satisfied unless special
algorithmic provisions are made. Without discussing this issue in
much detail, which goes well beyond the scope of this user's guide
(for example, see Tóth (2000) and references therein), we will
remind the user that there are three commonly accepted methods to enforce
the
condition, a strict physical law, is very hard
to satisfy in discrete computations. Being only an initial condition
of the MHD equations, it enters the equations indirectly and is not,
therefore, guaranteed to be generally satisfied unless special
algorithmic provisions are made. Without discussing this issue in
much detail, which goes well beyond the scope of this user's guide
(for example, see Tóth (2000) and references therein), we will
remind the user that there are three commonly accepted methods to enforce
the
![]() condition: the elliptic projection method (Brackbill
and Barnes, 1980), the constrained transport method (Evans and
Hawley, 1988), and the truncation-level error method
(Powell et al., 1999).
In the current release, the truncation-error cleaning
methods is provided for the eight-wave MHD unit,
and the constrained transport method is implemented for the
unsplit staggered mesh MHD units
(see Sec:usm_algorithm for details).
condition: the elliptic projection method (Brackbill
and Barnes, 1980), the constrained transport method (Evans and
Hawley, 1988), and the truncation-level error method
(Powell et al., 1999).
In the current release, the truncation-error cleaning
methods is provided for the eight-wave MHD unit,
and the constrained transport method is implemented for the
unsplit staggered mesh MHD units
(see Sec:usm_algorithm for details).
In the truncation-error method, the solenoidality of the magnetic
field is enforced by including several terms proportional to
![]() .
This removes the effects of unphysical magnetic tension forces parallel
to the field and stimulates passive advection of magnetic monopoles, if
they are spuriously created. In many applications, this method has been
shown to be an efficient and sufficient way to generate solutions of high
physical quality. However, it has also been shown (Tóth, 2000) that
this method can sometimes, for example in strongly discontinuous and
stagnated flows, lead to accumulation of magnetic monopoles, whose
strength is sufficient to corrupt the physical quality of computed
solutions. In order to eliminate this deficiency, the eight-wave MHD code
also uses a simple yet very effective method originally due to
Marder (1987) to destroy the magnetic monopoles on the scale on which
they are generated. In this method, a diffusive operator proportional
to
.
This removes the effects of unphysical magnetic tension forces parallel
to the field and stimulates passive advection of magnetic monopoles, if
they are spuriously created. In many applications, this method has been
shown to be an efficient and sufficient way to generate solutions of high
physical quality. However, it has also been shown (Tóth, 2000) that
this method can sometimes, for example in strongly discontinuous and
stagnated flows, lead to accumulation of magnetic monopoles, whose
strength is sufficient to corrupt the physical quality of computed
solutions. In order to eliminate this deficiency, the eight-wave MHD code
also uses a simple yet very effective method originally due to
Marder (1987) to destroy the magnetic monopoles on the scale on which
they are generated. In this method, a diffusive operator proportional
to
![]() is added to the induction equation, so that the
equation becomes
is added to the induction equation, so that the
equation becomes
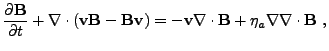 |
(15.30) |
As an alternative way to eliminate magnetic monopoles completely, the FLASH2 code includes an elliptic projection method, in which the unphysical divergence of the magnetic field can be removed to any desired level down to machine precision. As yet, this method has not been made available in FLASH4 and will be supported in a later release.
where
![]() is the electric field,
is the electric field,
![]() the magnetic field,
the magnetic field,
![]() the plasma velocity,
the plasma velocity,
![]() the current density,
the current density, ![]() the electron number density,
the electron number density, ![]() the electron charge,
the electron charge, ![]() the electron pressure,
the electron pressure, ![]() is Boltzmann's constant,
is Boltzmann's constant,
![]() the unit vector in the direction of the magnetic field,
the unit vector in the direction of the magnetic field,
![]() the electron plasma frequency,
the electron plasma frequency,
![]() the permittivity of vacuum,
the permittivity of vacuum, ![]() the electron-ion collision time,
the electron-ion collision time, ![]() the electron temperature, and
the electron temperature, and ![]() and
and ![]() are respectively the resistivity and the thermoelectric coefficients in dimensionless form.
are respectively the resistivity and the thermoelectric coefficients in dimensionless form.
Each of these terms can be enabled or disabled in FLASH at run time via the flash.par file. For example, a typical flash.par file for extended MHD runtime parameters should look more or less like this:
# Hall effect ----------------------------------------- use_Hall = .true. # Biermann battery (Source implementation)------------- use_Biermann = .true. hy_biermannSource = .true. # Biermann battery (Flux implementation)------------- use_Biermann = .true. # Biermann battery (Flux implementation with thermal magnetic wave term)------------- use_Biermann = .true. use_Biermann3T = .true. # Magnetic Resistivity -------------------------------- useMagneticResistivity = .true. resistivitySolver = "explicit" resistivityForm = "fullaniso" useCrossMagRes = .true. # the eta_wedge term # Thermoelectric Terms -------------------------------- use_Seebeck = .true. use_CrossField = .true. use_Nernst = .true.
One way of simulating a diffusive process is to add those physics units in a simulation Config file. For example, a snippet of Config file can look like this:
# Diffusive time step calculation and implicit solver(s) REQUIRES physics/Diffuse/DiffuseMain/Unsplit # Magnetic Resistivity REQUIRES physics/materialProperties/MagneticResistivity/MagneticResistivityMain/DaviesWen # Thermoelectric REQUIRES physics/materialProperties/Thermoelectric/ThermoelectricMain/DaviesWen
For Hall effect, Biermann battery, and Thermoelectric transport, there is no specific units to add, the only requirement is to require "source/physics/Hydro/HydroMain/unsplit/MHD_StaggeredMesh" (+usm) and for Biermann battery the MultiTemp implementation (+3t). Typically, for HEDP simulations, the setup will be done using "+usm3t". Also, for realistic Thermoelectric transport, a coefficients implementation should be chosen in the Config file as shown above. Below we detail the Hall, Biermann, Resistivity, and Thermoelectric implementations.
As indicated above (15.3.5), the user needs to include at least the Unsplit Staggered Mesh MHD solver ("+usm" during setup) in order to call the Hall implementation. Then the runtime parameter use_Hall has to be set to = .true.. Adding the Hall effect in the MHD model introduces two new kind of waves (see 15.3.5.1.5) that need to be taken into account for stability. It is why the cfl runtime parameter will generally have to be modified by the user for simulations including Hall physics. It is common for Hall simulations to use cfl values smaler than 0.1. The Hall effect is available in FLASH in 1D/2D/3D Cartesian geometries as well as in 2D Cylindrical geometry. We also require the user to set the runtime parameter conserveAngField to =.true. when using Hall effect in 2D cylindrical geometry.
Implementing the Hall effect in a MHD code consists to add one term in the induction equation:
where each electric field is obtained from the generalized Ohm's law.
![]() is the inductive electric field,
is the inductive electric field,
![]() is the electric field associated to the existence of friction between electrons and ions (one component of this field, and the one implemented in the FLASH code, is the ohmic electric field
is the electric field associated to the existence of friction between electrons and ions (one component of this field, and the one implemented in the FLASH code, is the ohmic electric field
![]() ),
),
![]() is the Biermann electric field (discussed in the next section) and finally:
is the Biermann electric field (discussed in the next section) and finally:
is the Hall electric field. We note that other fields exist in the generalized ohm's law (inertial...) but are not described here.
Because the electrical current
![]() is defined as
is defined as
![]() , the sum of the inductive and Hall terms can be written as
, the sum of the inductive and Hall terms can be written as
![]() . This indicates that the "frozen-in" behavior is actually valid only for the electron population. However, in many cases (see next section), it is a good approximation to consider the field to be frozen in the bulk (ion) population. Here we are interested in cases where this approximation fails and thus where the presence of the Hall term is necessary.
. This indicates that the "frozen-in" behavior is actually valid only for the electron population. However, in many cases (see next section), it is a good approximation to consider the field to be frozen in the bulk (ion) population. Here we are interested in cases where this approximation fails and thus where the presence of the Hall term is necessary.
In FLASH, the Hall effect is implemented by updating the face-centered fluxes for magnetic field and total energy equations. By firt writing the magnetic energy equation (in cgs):
we notice that the Hall electric field is not responsible for energy generation source
![]() and only the Poynting vector (
and only the Poynting vector (
![]() ) is affected by the presence of this additional electric field. This specificity of the Hall effect means that there is no need to modify other equations in the MHD model in order to satisfy total energy conservation (something we will have to do for Biermann). The Poynting contribution is added in FLASH in the face-centered total energy fluxes. Below we detail the flux formulation for the magnetic field equation, both in cartesian and cylindrical coordinates.
) is affected by the presence of this additional electric field. This specificity of the Hall effect means that there is no need to modify other equations in the MHD model in order to satisfy total energy conservation (something we will have to do for Biermann). The Poynting contribution is added in FLASH in the face-centered total energy fluxes. Below we detail the flux formulation for the magnetic field equation, both in cartesian and cylindrical coordinates.
In cartesian coordinates, the induction equation 15.32 can be written as:
or equivalently, using matrix notation:
where the flux matrix is expressed in terms of the electric field components:
with the tensor divergence defined as
![]() .
.
Expressing the Hall electric field components (from 15.33):
the Hall flux matrix is explicitly given by:
In cylindrical (r,![]() ,z) coordinates, the induction equations 15.32 writes as:
,z) coordinates, the induction equations 15.32 writes as:
which can be written as:
the "source term" on the right side here (often called "geometrical" source term) comes from the fact that we can write
![]() . Eq.15.41 can also be written without including the source term and rather having everything written in terms of fluxes. It's actually what is being done currently in FLASH and that's why it requires the user to set the runtime parameter conserveAngField to = .true. for the 2D cylindrical case.
. Eq.15.41 can also be written without including the source term and rather having everything written in terms of fluxes. It's actually what is being done currently in FLASH and that's why it requires the user to set the runtime parameter conserveAngField to = .true. for the 2D cylindrical case.
The Hall electric field in 2D axisymmetric cylindrical is explicitely given by:
As mentionned before, the addition of the Hall term in the MHD model is responsible for the possibility for the plasma to sustain two additional propagation modes. The phase velocity of these modes are computed in Hydro_computeDt.F90 and compared with other present speeds (sound, Alfven, fast and slow magneto-acoustic...) to deterine the temporal time step dt. To study the possibility for the plasma to generate Hall-induced waves, we keep only the Hall term in the induction equation and express it in this form:
the first right side term is responsible for the generation of the so called "Whistler waves" whereas the second term is responsible for the generation of the "Hall drift waves".
It is easy to show that (see Huba, 2003), applying the plane wave perturbation on equation 15.43 as well as using the Maxwell-Ampere law in the non-relativistic limit (
![]() ), the dispersion relation (in parallel propagation) for the whistler waves is given by:
), the dispersion relation (in parallel propagation) for the whistler waves is given by:
It can be clearly seen from this relation that the Whislter waves (Hall-induced) will become faster than the Alfven waves (inductively-induced) if
![]() or expressed in an other way if the spatial scale of the perturbation (
or expressed in an other way if the spatial scale of the perturbation (
![]() ) is smaller than the ion inertial length
) is smaller than the ion inertial length ![]() . This demonstrate why hall physics becomes really relevant for a physical problem on scales smaller than
. This demonstrate why hall physics becomes really relevant for a physical problem on scales smaller than ![]() .
.
By looking at the second right side term in equation 15.43, it can be shown that the Hall drift waves propagates in inhomogeneous plasmas and in the
![]() direction (assumed to be the direction of the
direction (assumed to be the direction of the
![]() vector). A simple dispersion relation can be obtained in the limit
vector). A simple dispersion relation can be obtained in the limit
![]() :
:
with
![]() being the spatial scale of the density gradient. Here again, the Hall-induced Hall drift waves will propagates faster than the Alfven speed only if
being the spatial scale of the density gradient. Here again, the Hall-induced Hall drift waves will propagates faster than the Alfven speed only if
![]() , that is to say if the spatial scale of the density gradient is smaller than the ion inertial length.
, that is to say if the spatial scale of the density gradient is smaller than the ion inertial length.
As indicated above (15.3.5), the user needs to include the Unsplit Staggered Mesh MHD solver ("+usm" during setup) in order to call the Biermann implementation. We currently offer support only for the 3T implementation ("+3t" during setup). Users wanting to use Biermann should thus setup their simulation with "+usm3t". Then the runtime parameter hy_useBiermann has to be set to = .true.. Two different versions of the Biermann battery mechanism are currently available in FLASH: a source version which should be considered as the most robust and reliable implementation as well as a flux-based version which should be used for specific problems with user-specified boundaries conditions. To use the source version, the user needs to set the runtime parameter hy_biermannSource to = .true. whereas for the flux-based version this runtime parameter should remain set to its default value of = .false.. A strong difference between the two versions lies in the fact that the flux-based one can introduce a new kind of thermal magnetic wave and thus new stability considerations that have to be taken into account by the user through the runtime parameter cfl. The term associated with this wave can be turned on or off with the logical runtime parameter use_Biermann3T. The Biermann battery mechanism, for both versions, is available in FLASH in 2D Cartesian and 2D Cylindrical geometries, but only the flux-based version will work accurately in 3D Cartesian. We also require the user to set the runtime parameter conserveAngField to =.true. when using Biermann battery mechanism in 2D cylindrical geometry. Finally, we recommand to the user to always set the runtime parameter shockDetect to = .true. with the consequence of removing Biermann B-field generation in cells tagged as shock.
Implementing the Biermann battery mechanism in a MHD code consists of adding terms in the induction equation as well as in the internal energy equations. Regarding only the Biermann term, the induction equation writes (see eq.15.32) as:
with the Biermann electric field given by:
This mechanism describes the possibility for a plasma to self-generate magnetic fields if there exist some crossed gradients of density and temperature. It can be seen by rewriting eq.15.46 (and inserting 15.47) as:
From this last equation it's also clear that Biermann-generated B-fields will be possible only in 2D and 3D geometries. As mentionned above, including Biermann in a MHD model should always be accompanied by the addition of one or several terms in the internal energy equations because of energy conservation considerations. This can be understood by looking at the magnetic energy equation (eq.15.34) and noting that the Biermann electric field is responsible for a source term
![]() . To maintain the conservation of total energy, one can then understand that this source terms must be compensated somewhere in another form of energy sink (where does the energy necessary to generate the B-fields comes from ?). This point is addressed in two different ways in FLASH:
. To maintain the conservation of total energy, one can then understand that this source terms must be compensated somewhere in another form of energy sink (where does the energy necessary to generate the B-fields comes from ?). This point is addressed in two different ways in FLASH:
It is then easy to show that with such an equation for electron internal energy and in the presence of ![]() in the Ohm's law, the total energy equation (magnetic + kinetic + internal) can be written in a fully conservative form. As we will demonstrate in 15.3.5.2.5, the addition of these new terms introduces a new kind of wave: the Thermal-magnetic waves and a corresponding phase velocity that needs to be taken into account for stability.
in the Ohm's law, the total energy equation (magnetic + kinetic + internal) can be written in a fully conservative form. As we will demonstrate in 15.3.5.2.5, the addition of these new terms introduces a new kind of wave: the Thermal-magnetic waves and a corresponding phase velocity that needs to be taken into account for stability.
Using the formalism described in 15.3.5.1.3, we write explicitely the Biermann electric field in cartesian coordinates:
and thus the Biermann flux matrix is explicitly given by:
Assuming the electric field being composed only of the Biermann one, from 15.40 and in the case of an axisymmetric configuration (
![]() = 0), eq.15.41 can be written as (here
= 0), eq.15.41 can be written as (here
![]() ):
):
In this case also we require the user to set the runtime parameter conserveAngField to = .true. for the 2D cylindrical case. It can be seen that in this geometry only a ![]() magnetic field can be generated. The Biermann electric field in 2D axisymmetric cylindrical is explicitely given by:
magnetic field can be generated. The Biermann electric field in 2D axisymmetric cylindrical is explicitely given by:
As mentionned previously, the flux version of Biermann (see 15.3.5.2.2) allows the propagation of a new kind of waves: the Thermal-magnetic waves (Pert, 1977). To derive the dispersion relation of these waves, suppose a cyldrincal axisymmetric situation where the density depends only on the coordinate r whereas the background temperature is homogeneous. Then consider this set of equations:
where we assumed
![]() . Then we apply perturbation theory in cylindrical coordinates (with
. Then we apply perturbation theory in cylindrical coordinates (with
![]() and
and
![]() ):
):
Considering plane waves
![]() , we get:
, we get:
and we finally get the dispersion relation for the Thermal-magnetic waves:
from which we can identify the phase velocity ![]() of Thermal-magnetic waves:
of Thermal-magnetic waves:
where
![]() is the ion speed of sound,
is the ion speed of sound, ![]() is the ion inertial length and
is the ion inertial length and
![]() is the characteristic length scale of the density gradient. It can clearly be seen that the Thermal-magnetic waves will be come faster than sound waves on scales smaller than the ion inertial length, in a similar way whistler amd Hall drift waves become faster than Alfven waves on this same scale. These non-dispersive waves propagate in inhomogeneous plasmas on iso-density surfaces. In FLASH, the time step related to this new caracteristic speed is computed in Hydro_computeDt.F90 and compared with others speeds in order to get the stable correct global time step. The cfl condition will generally have to be lowered in the presence of the flux-based version of Biermann.
is the characteristic length scale of the density gradient. It can clearly be seen that the Thermal-magnetic waves will be come faster than sound waves on scales smaller than the ion inertial length, in a similar way whistler amd Hall drift waves become faster than Alfven waves on this same scale. These non-dispersive waves propagate in inhomogeneous plasmas on iso-density surfaces. In FLASH, the time step related to this new caracteristic speed is computed in Hydro_computeDt.F90 and compared with others speeds in order to get the stable correct global time step. The cfl condition will generally have to be lowered in the presence of the flux-based version of Biermann.
# For Constant resistivity REQUIRES physics/materialProperties/MagneticResistivity/MagneticResistivityMain/Constant # For SpitzerHighZ resistivity REQUIRES physics/materialProperties/MagneticResistivity/MagneticResistivityMain/SpitzerHighZ # For DaviesWen resistivity REQUIRES physics/materialProperties/MagneticResistivity/MagneticResistivityMain/DaviesWen
See 23.2 for more details on each coefficients implementation.
It is important for the user to know that for all implementions the quantity actually computed and used is the magnetic diffusivity (in units of
![]() ).
Therefore, in the standard FLASH unit system (CGS), the value of the resistivity parameter should be in
).
Therefore, in the standard FLASH unit system (CGS), the value of the resistivity parameter should be in
![]() .
In the case of user-specific implementations of the “MagneticResistivity.F90" and “MagneticResistivity_fullState.F90" files, the values returned to the code should also always be in units of
.
In the case of user-specific implementations of the “MagneticResistivity.F90" and “MagneticResistivity_fullState.F90" files, the values returned to the code should also always be in units of
![]() .
.
There are three parameters that control how resistive MHD is solved in the code:
resistivityForm, useCrossMagRes, and resistivitySolver.
The resistivityForm parameter accepts values of “parallel", “perpendicular" (default),
or “fullaniso", and this controls the form of the resistivity terms in the generalized Ohm's law (eq. 15.31.
A value of “parallel" solves
![]() ,
and a value of “perpendicular" solves
,
and a value of “perpendicular" solves
![]() .
A value of “fullaniso" will solve
.
A value of “fullaniso" will solve
![]() .
Note that this has been rewritten as compared to eq. 15.31.
When useCrossMagRes is set to .true.,
the
.
Note that this has been rewritten as compared to eq. 15.31.
When useCrossMagRes is set to .true.,
the
![]() term is included and solved for by adding it to the Hall term.
term is included and solved for by adding it to the Hall term.
The resistivitySolver parameter accepts values of “explicit" (default), “implicit", or “hybrid". This controls which type of solver(s) is being used to solve the resistive terms. The explicit solver is a flux-based approach, and requires that the time step be limited for numerical stability. Thus, when using this explict solver, the user should always set useDiffuse and useDiffuseComputeDtMagnetic to .true. (as well as give a reasonable value to dt_diff_factor). See 19.1.6 for details on the implicit solver and how to use it, but note that the implicit solver is currently limited to only work generally on the uniform grid implementation (setup shortcut +ug).
The “hybrid" solver splits the resistive terms and solves
![]() implicitly, while solving
implicitly, while solving
![]() explicitly.
Hence it only makes sense to use the hybrid solver with resistivityForm = "fullaniso".
explicitly.
Hence it only makes sense to use the hybrid solver with resistivityForm = "fullaniso".
The same runtime parameters also turn on/off analogous terms in the heat flux equation: