25.1 Multigroup Diffusion

The radiative transfer (25.1) and electron energy (25.2) equations can be simplified using a multigroup diffusion approximation. The frequency space is divided into $N_g$ groups with $N_{g+1}$. Group $g$ is defined by the frequency range from $\nu_g$ to $\nu_{g+1}$. The plasma is assumed to emit radiation in a Planck spectrum with a given emission opacity. The multigroup diffusion equations solved by FLASH are

$$\frac{1}{c} \frac{\partial u_g}{\partial t} - \nabla \cdot \left(... ... u_g = \sigma_{e,g} a T_e^4 \frac{15}{\pi^4} \left[ P(x_{g+1}) - P(x_g) \right]$$ (25.3)

$${} \frac{1}{c} \frac{\partial u_e}{\partial t} = \sum_g \left\{ \... ...igma_{e,g} a T_e^4 \frac{15}{\pi^4} \left[ P(x_{g+1}) - P(x_g) \right] \right\}$$ (25.4)

where $u_g$ is the radiation energy density, $\sigma_{t,g}$ is the transport opacity, $\sigma_{a,g}$ is the absorption opacity, $\sigma_{e,g}$ is the emission opacity, $a$ is the radiation constant, $T_e$ is the electron temperature, and $P(x)$ is the Planck integral, defined below. The argument to the Planck integral, is $x = h\nu/k_BT_e$ where $h$ is Planck's constant and $k_B$ is the Boltzmann constant. The opacities in (25.3) and (25.4) are in units of $1/\textrm{cm}$ and $\sigma = \rho \kappa$. The Planck integral, $P(x)$ is defined as

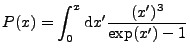$$P(x) = \int_0^x \textrm{d}x' \frac{ (x')^3 }{ \exp(x') -1 }$$ (25.5)

The multigroup diffusion equation and electron internal energy equation are operator-split using an explicit treatment. Thus, on each time step (25.4) is solved for each energy group using coefficients evaluated at time level $n$ using an implicit treatment for the diffusion solution itself. The equation below shows how the multigroup equations are discretized in time

$$\frac{1}{c} \frac{ u_g^{n+1} - u_g^n}{\Delta t} - \nabla \cdot \l... ...gma_{e,g}^n a (T_e^n)^4 \frac{15}{\pi^4} \left[ P(x_{g+1}^n) - P(x_g^n) \right]$$ (25.6)

$${} \frac{u_e^{n+1}-u_e^n}{\Delta t} = \sum_g \left\{ \sigma_{a,g}... ...^n a (T_e^n)^4 \frac{15}{\pi^4} \left[ P(x_{g+1}^n) - P(x_g^n) \right] \right\}$$ (25.7)

where the $n$ superscript denotes the time level, and $\Delta t$ is the time step length. These equations are solved on each time step. The diffusion coefficient, $D_g^n$, has been introduced. When no flux-limiter is employed, $D_g^n = 1/3 \sigma_{t,g}^n$. The flux-limiter limits the radiation flux in each group to the free streaming limit, $c u_g^n$. Several flux limiter options are available in FLASH. These are described in section 19.1.3. The string runtime parameter rt_mgdFlMode controls the flux limiter mode. The maximum flux is set to $q_\mathrm{max} = \alpha_r c u_g^n$ for each energy group. The coefficient $\alpha_r$ is set to one by default, which is what is physically most realistic. However, it can be controlled using the runtime parameter rt_mgdFlCoef.

The diffusion equation, (25.6), is an implicit equation and is solved using the general implicit diffusion solver described in section 19.1.2. It is recommended that users familiarize themselves with the general implicit diffusion solver to learn more about using MGD in FLASH.

The planck integral in previous versions has significant error and can be negative for $x<4 \times 10^{-4}$. Set rt_planckIntMethod to 0 (by default) to use the method in old versions. Set rt_planckIntMethod to a positive number to use the new method: mininum of the $m$-th order expansion as $\exp^{-x} \to 0$ and the $n$-th order expansion as $x \to 0$. Current available options: set to $213$ for $m=2$ and $n=13$, set to $321$ for $m=3$ and $n=21$, set to $621$ for $m=6$ and $n=21$.

25.1.1 Using Multigroup Radiation Diffusion

This section describes how to use MGD in FLASH. Section 35.7.5 shows an example of how to use MGD in a realistic HEDP simulation and is extremely informative.

Several setup options are needed to use MGD. The +mgd setup shortcut will include the MGD unit in the simulation. In addition, storage needs to be created for storing the specific energy for each group. This is done using the mgd_meshgroups setup variable. The user must set mgd_meshgroups such that:

$$\textrm{(mgd\_meshgroups)} N_\textrm{mesh} \ge N_g$$ (25.8)

where $N_\textrm{mesh}$ represents the number of meshes (please see section 25.1.2 for more information). If you don't know what this is, you can assume that $N_\textrm{mesh} = 1$. In this case, the constraint is that the mgd_meshgroups setup variable must be greater than or equal to the number of energy groups. The actual number of energy groups, $N_g$, is set at run time using the runtime parameter rt_mgdNumGroups. Thus, as an example, the setup options for a 4-group simulation could be:  

+mgd mgd_meshgroups=6

and the runtime parameter file must contain rt_mgdNumGroups = 4. No changes are needed to the Config file of the simulation.

The FLASH checkpoint files will contain the specific energy in each radiation energy group for each cell. The variables are named r### where ### is a three digit number from one to $N_g$. Users can also add these variables to the list of plot variables so they will be included in plot files.

Several runtime parameters are used to control the MGD unit. The runtime parameter rt_useMGD must be set to .true. for MGD simulations. The energy group structure (values of the group boundaries) are specified, manually, using runtime parameters. A simulation with $N_g$ groups will have $N_g+1$ energy group boundaries. These are set using the rt_mgdBounds_### runtime parameters, where ### is a number between 1 and $N_g+1$. By default, enough runtime parameters exist for specifying 101 energy group boundaries. In the case that more groups are needed, the mgd_maxgroups setup variable sets the number of group boundary runtime parameters. For example, if 200 energy groups are needed, then mgd_maxgroups=200 should be specified on the setup line. If $N_g \le 100$, no action is needed.

When MGD is in use, the Opacity unit provides opacities for each cell. Thus, the useOpacity runtime parameter must be set to true and the appropriate opacity model must be specified. Please see section 23.5 for a detailed description on how to use the Opacity unit in FLASH.

Finally, the radiation boundary conditions must be specified using runtime parameters. The parameters:  

rt_mgdXlBoundaryType
rt_mgdXrBoundaryType
rt_mgdYlBoundaryType
rt_mgdYrBoundaryType
rt_mgdZlBoundaryType
rt_mgdZrBoundaryType

control the boundary condition on each logical face of the domain. The allowed values are:

• reflecting, neumann: This is a zero-flux, or Neumann boundary condition and should be used to model reflecting boundaries
• dirichlet: This (poorly named) value represents a fixed radiation temperature boundary condition
• vacuum: This represents a vacuum boundary condition

Please see section 19.1.2.1 for more information on boundary conditions for the diffusion solver.

As was mentioned earlier, FLASH uses the generalized implicit diffusion solver, described in section 19.1.2, to solve (25.6) for each energy group. Thus, users must make sure to include an appropriate diffusion solver in their simulation.

25.1.2 Using Mesh Replication with MGD

When many energy groups are needed, domain decomposition alone is not an effective method for speeding up calculations. The computation time scales roughly linearly with the number of energy groups. As the number of groups increases, users can divide the mesh among larger number of processors to compensate. This is an effective strategy until the strong scaling limit for the simulation is reached. At this point, mesh replication becomes the only way to speed up the simulation further.

Mesh replication allows FLASH to perform the diffusion solves for each energy group in parallel. By default, mesh replication is deactivated and each diffusion equation is solved serially. When mesh replication is in use the total pool of $N_p$ processes is divided among $N_m$ identical copies of the computational mesh. The radiation solver uses these copies of the mesh to perform $N_m$ parallel radiation solves. The runtime parameter meshCopyCount is used to set $N_m$ and has a value of 1 by default.

This is best illustrated with an example. Suppose $N_g$, the total number of energy groups, is set to 100, and there are $N_p = 6$ processes available to run the simulation. If meshCopyCount=1, then $N_m = 1$ and the computational mesh will not be replicated. This is FLASH's normal mode of operation: the mesh will be divided into six pieces and each process will be responsible for one of these pieces. Each process will also be involved in the solution of the diffusion equation for all 100 energy groups. If meshCopyCount=2, then the computational domain will be divided into three pieces. Two processes will be assigned to each piece. In other words two groups of three processes will be created. The first set of three processes will be responsible for solving the diffusion equations for the odd numbered energy groups. The second set of processes will solve the diffusion equations for the even numbered energy groups. Each process only knows about 50 of the 100 groups. In some cases, this may be substantially faster than the meshCopyCount=1 approach.

Another benefit of mesh replication is that it reduces the amount of memory needed per process. In the example above, when meshCopyCount=1, each process must store the energy density for all 100 energy groups. Thus, storage must exist for 100 cell centered variables on each process. When meshCopyCount=2, storage is only needed for 50 cell centered variables. The setup variable mgd_meshgroups controls the number of cell centered variables created on process. Thus, when meshCopyCount=2, we can set mgd_meshgroups to 50 instead of 100. As a result, far less memory is used per block.

Whether or not mesh replication is helpful for a particular simulation can only be determined through extensive testing. It depends on the particular simulation and the hardware.

25.1.3 Specifying Initial Conditions

The initial conditions must be specified throughout the domain for each radiation energy group. This involves setting the specific energy, $e_g = u_g/\rho$, in units of erg/g for each group. Because of the mesh replication capability, the user is discouraged from manually setting the value of the underlying radiation mass scalars. Instead, several routines have been added to the RadTrans unit to simplify this process dramatically. Specifying the initial conditions involves two steps. First, the value of $e_g$ must be set for each group in each cell. Second, either the total specific radiation energy, $e_r = \sum_g e_g$, or the radiation temperature, $T_r = (u_r/a)^{1/4}$, must be set - depending on the value of eosModeInit. Below, two use cases are described.

25.1.3.1 Initializing using a Radiation Temperature

The easiest way to set the initial condition is to use a radiation temperature in each cell and to assume that the radiation field is described by a Planck spectrum. The subroutine:

 

RadTrans_mgdEFromT(blockId, axis, trad, tradActual)

will automatically set the value of $e_g$ for each group using a given radiation temperature and assuming a black body spectrum. The arguments are:

1. blockId: The block ID
2. axis: A 3 dimensional array of integers indicating the cell within the block
3. trad: An input, the desired radiation temperature
4. tradActual: An output, The actual radiation temperature (described further below)

When the simulation is initialized, it is important that $T_r = (\sum_g u_g/a)^{1/4}$. This will not always be the case. The reason is that a black body spectrum has a non zero energy density for all frequencies. But FLASH simulations require finite energy group boundaries. For example, if trad is set to 11604 K (this corresponds to 1 eV), but the upper energy group boundary is only set to 10 eV, then we are effectively cutting off the part of the spectrum above 10 eV. The actual radiation temperature, which is consistent with the sum of the energies in each group, will be slightly less than 1 eV. The argument tradActual contains this new radiation temperature.

Once RadTrans_mgdEFromT has been used to initialize $e_g$, either the total radiation specific energy, $e_r$, must be set or the radiation temperature for the cell must be specified. When the runtime parameter eosModeInit is set to “dens_temp_gather”, the initial radiation temperature must be specified in the variable TRAD_VAR. When eosModeInit is set to “dens_ie_gather”, $e_r$ must be specified in the variable ERAD_VAR.

The example below shows a segment from a Simulation_initBlock routine from a typical simulation which uses MGD:

 

do k = blkLimits(LOW,KAXIS),blkLimits(HIGH,KAXIS)
   do j = blkLimits(LOW,JAXIS),blkLimits(HIGH,JAXIS)
      do i = blkLimits(LOW,IAXIS),blkLimits(HIGH,IAXIS)


axis(IAXIS) = i
         axis(JAXIS) = j
         axis(KAXIS) = k


...


! Set the secific energy in each radiation group using a
         ! radiation temperature of 1 eV (11604.55 K): 
         call RadTrans_mgdEFromT(blockId, axis, 11604.55, tradActual)


! Set the radiation temperature:
         call Grid_putPointData(blockId, CENTER, TRAD_VAR, EXTERIOR, axis, tradActual)


! Alternatively, we could have set ERAD_VAR using a*(tradActual)**4


enddo
   enddo
enddo

Note that tradActual is used to specify the value of TRAD_VAR.

25.1.3.2 Manually setting the radiation spectrum

Specifying the radiation temperature is sufficient for many cases. Alternatively, users can manually specify the radiation spectrum. The subroutine

 

RadTrans_mgdSetEnergy(blockId, axis, group, eg)

has been created for this purpose. The arguments are:

• blockId: The block ID
• axis: A 3 dimensional array of integers indicating the cell within the block
• group: The group number, between $1$ and $N_g$
• eg: The specific radiation energy (erg/g) for the group

This subroutine sets the value of $e_g$ for a particular cell and should be called from the Simulation_initBlock subroutine.

The example below assumes that the user would like to initialize the radiation field so that $e_1 = a T_r^4/\rho$ and all other groups are initialized to zero energy. Note, that for this example, the user should obtain the value of $a$, the radiation constant, from the PhysicalConstants unit. This simulations used $N_g = 4$.

 

do k = blkLimits(LOW,KAXIS),blkLimits(HIGH,KAXIS)
   do j = blkLimits(LOW,JAXIS),blkLimits(HIGH,JAXIS)
      do i = blkLimits(LOW,IAXIS),blkLimits(HIGH,IAXIS)


axis(IAXIS) = i
         axis(JAXIS) = j
         axis(KAXIS) = k


...


! Set the secific energy in each radiation group:
         call RadTrans_mgdSetEnergy(blockId, axis, 1, a*sim_trad**4/sim_rho)
         call RadTrans_mgdSetEnergy(blockId, axis, 2, 0.0)
         call RadTrans_mgdSetEnergy(blockId, axis, 3, 0.0)
         call RadTrans_mgdSetEnergy(blockId, axis, 4, 0.0)


! Set the radiation temperature:
         call Grid_putPointData(blockId, CENTER, TRAD_VAR, EXTERIOR, axis, sim_trad)


! Alternatively, we could have set ERAD_VAR using a*sim_trad**4/sim_rho


enddo
   enddo
enddo

25.1.4 Altering the Radiation Spectrum

In some cases, it is necessary to alter the radiation spectrum manually, for example, to add a radiation energy source. In these cases, it is useful to manually alter the mesh variables which store the specific radiation energy within each group: $e_g = u_g/\rho$. However, because of mesh replication, altering these variables requires a different procedure than modifying other mesh variables (such as the density) in FLASH. The reason is that each process does not, in general, have access to each $e_g$. The procedure for modifying $e_g$ directly is as follows:

1. Loop over the energy groups that each process sees
2. Modify $e_g$
3. Modify the total specific radiation energy, $e_\mathrm{rad}$, so that it stores the sum over all $e_g$

Note, that in step 1, looping over the energy groups does not simply involve looping from 1 to $N_g$. The reason is that each process must loop over only those groups that it is responsible for. Again, because of mesh replication, this may be less than $N_g$. Below, an example is shown where the specific energy in each group is manually set to $10^{12}$ erg/g. An ideal place for this type of code to exist is in the Simulation_adjustEvolution subroutine which gets called every time step.  

! Loop over all cells, set the specific radiation energy to zero:
do lb = 1, nblk
  call Grid_getBlkIndexLimits(blklst(lb),blkLimits,blkLimitsGC)
  call Grid_getBlkPtr(blklst(lb), blkPtr)


do k = blkLimits(LOW,KAXIS), blkLimits(HIGH,KAXIS)
    do j = blkLimits(LOW,JAXIS), blkLimits(HIGH,JAXIS)
      do i = blkLimits(LOW,IAXIS), blkLimits(HIGH,IAXIS)
        blkPtr(ERAD_VAR,i,j,k) = 0.0
      end do
    end do
  end do
  call Grid_releaseBlkPtr(blklst(lb), blkPtr)
end do


! Loop over radiation energy groups:
do gloc = 1, NONREP_NLOCS(rt_acrossMe, rt_meshCopyCount, rt_mgdNumGroups)


! g represents the global energy group number:
  g = NONREP_LOC2GLOB(gloc, rt_acrossMe, rt_meshCopyCount)


! gvar represents the index in the block pointer for group g:
  gvar = MGDR_NONREP_LOC2UNK(gloc)


! Loop over blocks and set the energy density in each group:
  do lb = 1, nblk
    call Grid_getBlkIndexLimits(blklst(lb),blkLimits,blkLimitsGC)
    call Grid_getBlkPtr(blklst(lb), blkPtr)


do k = blkLimits(LOW,KAXIS), blkLimits(HIGH,KAXIS)
      do j = blkLimits(LOW,JAXIS), blkLimits(HIGH,JAXIS)
        do i = blkLimits(LOW,IAXIS), blkLimits(HIGH,IAXIS)


! Set the specific energy in group g:
          blkPtr(gvar,i,j,k) = 1.0e+12


! Make sure to track the total radiation energy in the cell:
          blkPtr(ERAD_VAR,i,j,k) = blkPtr(ERAD_VAR,i,j,k) + &
                                   blkPtr(gvar,i,j,k)
        end do
      end do
    end do
    call Grid_releaseBlkPtr(blklst(lb), blkPtr)
  end do
end do


! Finally, every process needs to know the total specific radiation
! energy. RadTrans_sumEnergy adds up ERAD_VAR across all of the
! meshes:
call RadTrans_sumEnergy(ERAD_VAR, nblk, blklst)


! Call EOS to get a consistent state:
do lb = 1, nblk
  call Grid_getBlkIndexLimits(blklst(lb),blkLimits,blkLimitsGC)
  call Eos_wrapped(MODE_DENS_EI_GATHER,blkLimits,blklst(lb))
end do

In the first part of the example, the value of ERAD_VAR is set to zero. ERAD_VAR simply stores the total specific radiation energy in each cell. After we are done modifying the energy for each group, it is important that ERAD_VAR be updated to contain the total specific radiation energy.

The second part of the example loops over the groups. Notice the strange loop ending index. The NONREP_NLOCS macro computes the number of groups represented on a given process. To find the actual group number, $g$, a call is made to NONREP_LOC2GLOB. Next, MGDR_NONREP_LOC2UNK is called to get the actual index into the block pointer which corresponds to group g. Following this is a fairly standard loop over blocks and cells where the block pointer is used to modify the specific energy in each group. Notice that we are keeping a running total of the total specific energy in the cell which is stored in ERAD_VAR.

Finally, we must call RadTrans_sumEnergy to add up ERAD_VAR across all of the meshes. After this call, every process will contain the same total specific energy in each cell. This is followed by a call to the equation of state. This is needed to update the radiation temperature and pressure, TRAD_VAR and ERAD_VAR, respectively.