Subsections
18.8 Circuit
The Circuit unit implements various routines for calculating current
supplied by an external circuit. The main purpose is to provide
a boundary condition for current-driven systems such as a Z-pinch.
There are two parameters that may be used by other units for such a boundary
condition: circ_IloadOld and circ_IloadNew. These represent
the current (in Amperes) at the current time step 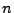 before Circuit is called
and the current at time step
before Circuit is called
and the current at time step 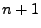 after Circuit has been called, respectively.
after Circuit has been called, respectively.
Some of the implementations will output useful information to a file named circuit.dat.
The subsections that follow describe the different implementations that are currently
included in FLASH. To activate a particular implemenation, include the appropriate path
in the Config file of your simulation directory.
18.8.1 Constant
In the Constant implementation is the simplest of the models and applies a constant
current to the load. A constant current is useful when considering ideal cases or if
actual data from a run is not available. A run time parameter that is defined by the
circcurrConstant variable sets the current. By setting this value in
the par file this constant current will be applied to the load for the duration of
the simulation.
This implementation lies in the physics/sourceTerms/Circuit/
CircuitMain/Constant directory.
18.8.2 FileInput
The FileInput implementation reads in current data from a file, interpolates the
data, and then applies the current to the load. The file input mode is useful when
the exact properties of the current delivered to the load are known, but not much
else about the system.
This unit works by taking in a run time parameter circcurrFile in
the flash.par which is the name of the file with the current and time data. The data
should be given in MegaAmperes and nanoseconds. The unit first checks to make sure
that the file exists. After running the check, a linear interpolation is used to
obtain the current values for the simulation time which is then the current that is
applied to the load.
This implementation lies in the physics/sourceTerms/Circuit/
CircuitMain/FileInput directory.
18.8.3 McBride
The McBride circuit model follows the work done by McBride et al Phys. Rev. ST Accel.
Beams 13, 120401, 20102. This model is a purely reactive model that allows an input
current which will be applied to a dynamic load.
Figure 18.21:
Schematic showing the circuit
that is being solved in the McBride implemenation.
|
|
This unit works by taking in a run time parameter circvoltFile in the
flash.par which is the name of the file with the voltage and time data. The data
should be given in Amps and seconds. As in FileInput, this unit checks if the file
exists and then linearly interpolates the data. The obtained voltage is then applied
as Voc to the following circuit LC circuit as seen in Figure 18.21.
To calculate the current that is applied to the load the following equations are solved:
![$\displaystyle \begin{pmatrix}
\frac{dV_c}{dt} [6pt]
\frac{dI_{stack}}{dt} ...
...
\frac{-V_c-Z_o I_{stack}+V_{oc}}{L} [6pt]
\frac{V_c-V_t}{L_o}
\end{pmatrix}.$](img1980.png) |
(18.280) |
Vt can be rewritten as
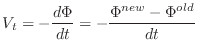 |
(18.281) |
where 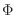 is the magnetic flux in the domain. In the case of a one dimensional
cylindrical domain there is a run time parameter circcylLength which is the
length of the cylinder used for the flux calculation. The axial load current that is
determined from the circuit model is used with Ampere’s Law to define the azimuthal
magnetic field on the upper-r domain boundary. This field is used as a boundary
condition for the implicit magnetic resistivity (diffusion) solver.
is the magnetic flux in the domain. In the case of a one dimensional
cylindrical domain there is a run time parameter circcylLength which is the
length of the cylinder used for the flux calculation. The axial load current that is
determined from the circuit model is used with Ampere’s Law to define the azimuthal
magnetic field on the upper-r domain boundary. This field is used as a boundary
condition for the implicit magnetic resistivity (diffusion) solver.
This implementation lies in the physics/sourceTerms/Circuit/CircuitMain/McBride directory.
18.8.4 CESZAR
The Ceszar circuit model replicates a simplified model of the Ceszar Linear
Transformer Driver. Unlike the McBride model, this model is both reactive and
resistive driven by a discharging capacitor specified by its initial voltage.
The target is a dynamic load.
Figure 18.22:
Schematic showing the circuit
that is being solved in the Ceszar implemenation.
|
|
This unit works by taking in a run time parameter circCESZAR
V0 in the flash which defines the voltage across the capacitor in
Volts. To calculate the current applied to the load the following equations are solved:
![$\displaystyle \begin{pmatrix}
\frac{dI_s}{dt} [6pt]
\frac{dI_l}{dt} [6pt]
...
...]
\frac{I_s R - I_l (Z_l + R) - V_t}{L_l} [6pt]
\frac{-I_s}{C}
\end{pmatrix}.$](img1984.png) |
(18.282) |
Vt can be rewritten as
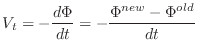 |
(18.283) |
where 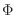 is the magnetic flux in the domain. In the case of a one dimensional
cylindrical domain there is a run time parameter circcylLength which is the
length of the cylinder. The axial load current that is determined from the circuit
model is used with Ampere’s Law to define the azimuthal magnetic field on the upper-r
domain boundary. This field is used as a boundary condition for the implicit magnetic
resistivity (diffusion) solver.
is the magnetic flux in the domain. In the case of a one dimensional
cylindrical domain there is a run time parameter circcylLength which is the
length of the cylinder. The axial load current that is determined from the circuit
model is used with Ampere’s Law to define the azimuthal magnetic field on the upper-r
domain boundary. This field is used as a boundary condition for the implicit magnetic
resistivity (diffusion) solver.
This implementation lies in the physics/sourceTerms/Circuit/CircuitMain/CESZAR directory.
![]() before Circuit is called
and the current at time step
before Circuit is called
and the current at time step ![]() after Circuit has been called, respectively.
after Circuit has been called, respectively.
![$\displaystyle \begin{pmatrix}
\frac{dV_c}{dt} [6pt]
\frac{dI_{stack}}{dt} ...
...
\frac{-V_c-Z_o I_{stack}+V_{oc}}{L} [6pt]
\frac{V_c-V_t}{L_o}
\end{pmatrix}.$](img1980.png)
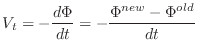
![$\displaystyle \begin{pmatrix}
\frac{dI_s}{dt} [6pt]
\frac{dI_l}{dt} [6pt]
...
...]
\frac{I_s R - I_l (Z_l + R) - V_t}{L_l} [6pt]
\frac{-I_s}{C}
\end{pmatrix}.$](img1984.png)