Next: 8.12 Unit Test Up: 8. Grid Unit Previous: 8.10 GridSolvers Contents Index
FLASH can use various kinds of coordinates (“geometries”) for modeling physical problems. The available geometries represent different (orthogonal) curvilinear coordinate systems.
The geometry for a particular problem is set at runtime (after an appropriate invocation of setup) through the geometry runtime parameter, which can take a value of "cartesian", "spherical", "cylindrical", or "polar". Together with the dimensionality of the problem, this serves to completely define the nature of the problem's coordinate axes (Table 8.9). Note that not all Grid implementations support all geometry/dimension combinations. Physics units may also be limited in the geometries supported, some may only work for Cartesian coordinates.
The core code of a Grid implementation is not concerned with the mapping of cell indices to physical coordinates; this is not required for under-the-hood Grid operations such as keeping track of which blocks are neighbors of which other blocks, which cells need to be filled with data from other blocks, and so on. Thus the physical domain can be logically modeled as a rectangular mesh of cells, even in curvilinear coordinates.
There are, however, some areas where geometry needs to be taken into consideration. The correct implementation of a given geometry requires that gradients and divergences have the appropriate area factors and that the volume of a cell is computed properly for that geometry. Initialization of the grid as well as AMR operations (such as restriction, prolongation, and flux-averaging) must respect the geometry also. Furthermore, the hydrodynamic methods in FLASH are finite-volume methods, so the interpolation must also be conservative in the given geometry. The default mesh refinement criteria of FLASH4 also currently take geometry into account, see Sec: refinement above.
| name | dimensions | support | axisymmetric | ||||
| cartesian | 1 | pm4,pm2,UG | n | ||||
| cartesian | 2 | pm4,pm2,UG | n | ||||
| cartesian | 3 | pm4,pm2,UG | n | ||||
| cylindrical | 1 | pm4,UG | y | ||||
| cylindrical | 2 | pm4,pm2,UG | y | ||||
| cylindrical | 3 | pm4,UG | n | ||||
| spherical | 1 | pm4,pm2,UG | y | ||||
| spherical | 2 | pm4,pm2,UG | y | ||||
| spherical | 3 | pm4,pm2,UG | n | ||||
| polar | 1 | pm4,UG | y | ||||
| polar | 2 | pm4,pm2,UG | n | ||||
|
3 | -- | n |
A convention:
in this section,
Small letters ![]() ,
, ![]() , and
, and ![]() are used with their usual meaning in
designating coordinate directions for specific coordinate systems:
i.e.,
are used with their usual meaning in
designating coordinate directions for specific coordinate systems:
i.e., ![]() and
and ![]() refer to directions in Cartesian coordinates,
and
refer to directions in Cartesian coordinates,
and ![]() may refer to a (linear) direction in either Cartesian
or cylindrical coordinates.
may refer to a (linear) direction in either Cartesian
or cylindrical coordinates.
On the other hand, capital symbols ![]() ,
, ![]() , and
, and ![]() are used to refer to the
(up to) three directions of any coordinate system, i.e.,
the directions corresponding to the
IAXIS, JAXIS, and KAXIS
dimensions in FLASH4, respectively.
Only in the Cartesian case do these correspond directly to
their small-letter counterparts. For other geometries,
the correspondence is given in Table 8.9.
are used to refer to the
(up to) three directions of any coordinate system, i.e.,
the directions corresponding to the
IAXIS, JAXIS, and KAXIS
dimensions in FLASH4, respectively.
Only in the Cartesian case do these correspond directly to
their small-letter counterparts. For other geometries,
the correspondence is given in Table 8.9.
In the context of FLASH, curvilinear coordinates are most useful with 1-d or 2-d simulations, and this is how they are commonly used. But what does it mean to apply curvilinear coordinates in this way? And what does it mean to do a 1D or a 2D simulation of threedimensional reality? Physical reality has three spatial dimensions (as far as the physical problems simulated with FLASH are concerned). In Cartesian coordinates, it is relatively straightforward to understand what a 2-d (or 1-d) simulation means: “Just leave out one (or two) coordinates.” This is less obvious for other coordinate systems, therefore some fundamental discussion follows.
A reduced dimensionality (RD) simulation can be naively understood as taking a cut (or, for 1-d, a linear probe) through the real 3-d problem. However, there is also an assumption, not always explicitly stated, that is implied in this kind of simulation: namely, that the cut (or line) is representative of the 3-d problem. This can be given a stricter meaning: it is assumed that the physics of the problem do not depend on the omitted dimension (or dimensions). A RD simulation can be a good description of a physical system only to the degree that this assumption is warranted. Depending on the nature of the simulated physical system, non-dependence on the omitted dimensions may mean the absence of force and/or momenta vector components in directions of the omitted coordinate axes, zero net mass and energy flow out of the plane spanned by the included coordinates, or similar.
For omitted dimensions that are lengths -- ![]() and possibly
and possibly ![]() in Cartesian,
and
in Cartesian,
and ![]() in cylindrical and polar RD simulations --
one may think of a 2-d cut as representing a (possibly very thin) layer
in 3-d space sandwiched between two parallel planes.
There is no a priori definition of the thickness of the layer,
so it is not determined what 3-d volume should be asigned to a 2-d cell
in such coordinates. We can thus arbitrarily assign the length “
in cylindrical and polar RD simulations --
one may think of a 2-d cut as representing a (possibly very thin) layer
in 3-d space sandwiched between two parallel planes.
There is no a priori definition of the thickness of the layer,
so it is not determined what 3-d volume should be asigned to a 2-d cell
in such coordinates. We can thus arbitrarily assign the length “![]() ”
to the edge length of a 3-d cell volume, making the volume equal
to the 2-d area.
We can understand generalizations of “volume” to 1-d, and of “face
areas” to 2-d and 1-d RD simulations with omitted linear coordinates,
in an equivalent way: just set the length of cell edges along omitted
dimensions to 1.
”
to the edge length of a 3-d cell volume, making the volume equal
to the 2-d area.
We can understand generalizations of “volume” to 1-d, and of “face
areas” to 2-d and 1-d RD simulations with omitted linear coordinates,
in an equivalent way: just set the length of cell edges along omitted
dimensions to 1.
For omitted dimensions that are angles -- the ![]() and
and ![]() coordinates
on spherical, cylindrical, and polar geometries --
it is easier to think of omitting an angle as the equivalent of integrating
over the full range of that angle coordinate (under the assumption that
all physical solution variables are independent of that angle).
Thus omitting an angle
coordinates
on spherical, cylindrical, and polar geometries --
it is easier to think of omitting an angle as the equivalent of integrating
over the full range of that angle coordinate (under the assumption that
all physical solution variables are independent of that angle).
Thus omitting an angle ![]() in these geometries implies
the assumption of axial symmetry, and this is noted in Table 8.9.
Similarly, omitting both
in these geometries implies
the assumption of axial symmetry, and this is noted in Table 8.9.
Similarly, omitting both ![]() and
and ![]() in spherical coordinates
implies an assumption of complete spherical symmetry.
When
in spherical coordinates
implies an assumption of complete spherical symmetry.
When ![]() is omitted, a 2-d cell actually represents the 3-d object
that is generated by rotating the 2-d area around a
is omitted, a 2-d cell actually represents the 3-d object
that is generated by rotating the 2-d area around a ![]() -axis.
Similarly, when only
-axis.
Similarly, when only ![]() is included, 1-d cells (i.e.,
is included, 1-d cells (i.e., ![]() intervals)
represent hollow spheres or cylinders.
(If the coordinate interval begins at
intervals)
represent hollow spheres or cylinders.
(If the coordinate interval begins at ![]() , the sphere or cylinder
is massive instead of hollow.)
, the sphere or cylinder
is massive instead of hollow.)
As a result of these considerations, the measures for cell (and block) volumes and face areas in a simulation depends on the chosen geometry. Formulas for the volume of a cell dependent on the geometry are given in the geometry-specific sections further below.
As discussed in Sec:PARAMESH flux conservation, to ensure conservation at a jump in refinement in AMR grids, a flux correction step is taken. The fluxes leaving the fine cells adjacent to a coarse cell are used to determine more accurately the flux entering the coarse cell. This step takes the coordinate geometry into account in order to accurately determine the areas of the cell faces where fine and coarse cells touch. By way of example, an illustration is provided below in the section on cylindrical geometry.
The following discussion applies to geometries with
omitted dimensions that are lengths -- ![]() and possibly
and possibly ![]() in Cartesian,
and
in Cartesian,
and ![]() in cylindrical and polar RD simulations.
We will consider Cartesian geometries as the most common case,
and just note that the remaining cases can be thought of analogously.
in cylindrical and polar RD simulations.
We will consider Cartesian geometries as the most common case,
and just note that the remaining cases can be thought of analogously.
In 2D Cartesian, the “volume” of a cell should be
![]() .
We would like to preserve the form of equations that relate extensive quantities
to their densities, e.g.,
.
We would like to preserve the form of equations that relate extensive quantities
to their densities, e.g.,
![]() for mass and
for mass and
![]() for total energy
in a cell. We also like to retain the usual definitions for
intensive quantities such as density
for total energy
in a cell. We also like to retain the usual definitions for
intensive quantities such as density ![]() , including
their physical values and units, so that material density
, including
their physical values and units, so that material density ![]() is expressed in
is expressed in ![]() (more generally
(more generally ![]() ),
no matter whether 1D, 2D, or 3D.
We cannot satisfy both desiderata without modifying the interpretation
of “mass”, “energy”, and similar extensive quantities in the
system of equations modeled by FLASH.
),
no matter whether 1D, 2D, or 3D.
We cannot satisfy both desiderata without modifying the interpretation
of “mass”, “energy”, and similar extensive quantities in the
system of equations modeled by FLASH.
Specifically, in a 2D Cartesian simulation, we have to interpret “mass”
as really representing a linear mass density, measured in ![]() .
Similarly, an “energy” is really a linear energy density, etc.
.
Similarly, an “energy” is really a linear energy density, etc.
In a 1D Cartesian simulation, we have to interpret “mass”
as really representing a surface mass density, measured in ![]() ,
and an “energy” is really a surface energy density.
,
and an “energy” is really a surface energy density.
(There is a different point of view, which amounts to the same thing:
One can think of the “mass” of a cell (in 2D) as the physical mass contained in a
threedimensional cell of volume
![]() where the
cell height
where the
cell height ![]() is set to be exactly 1 length unit. Always with the understanding that
“nothing happens” in the
is set to be exactly 1 length unit. Always with the understanding that
“nothing happens” in the ![]() direction.)
direction.)
Note that this interpretation of “mass”,“energy”, etc. must be taken into account not just when examining the physics in individual cells, but equally applies for quantities integrated over larger regions, including the “total mass” or “total energy” etc. reported by FLASH in flash.dat files -- they are to be interpreted as (linear or surface) densities of the nominal quantities (or, alternatively, as integrals over 1 length unit in the missing Cartesian directions).
The user chooses a geometry by setting the geometry runtime parameter in flash.par. The default is "cartesian" (unless overridden in a simulation's Config file). Depending on the Grid implementation used and the way it is configured, the geometry may also have to be compiled into the program executable and thus may have to be specified at configuration time; the setup flag -geometry should be used for this purpose, see Sec:ListSetupArgs.
The geometry runtime parameter is most useful in cases where the geometry does not have to be specified at compile-time, in particular for the Uniform Grid. The runtime parameter will, however, always be considered at run-time during Grid initialization. If the geometry runtime parameter is inconsistent with a geometry specified at setup time, FLASH will then either override the geometry specified at setup time (with a warning) if that is possible, or it will abort.
This runtime parameter is used by the Grid unit and also by hydrodynamics solvers, which add the necessary geometrical factors to the divergence terms. Next we describe how user code can use the runtime parameter's value.
#include "constants.h" integer :: geometry call Grid_getGeometry(geometry) select case (geometry) case (CARTESIAN) ! do Cartesian stuff here ... case (SPHERICAL) ! do spherical stuff here ... case (CYLINDRICAL) ! do cylindrical stuff here ... case (POLAR) ! do polar stuff here ... end select |
Coordinate information for the mesh can be determined via the Grid_getCellCoords routine. This routine can provide the coordinates of cells at the left edge, right edge, or center. The width of cells can be determined via the Grid_getDeltas routine. Angle values and differences are given in radians. Coordinate information for a block of cells as a whole is available through Grid_getBlkCenterCoords and Grid_getBlkPhysicalSize.
The volume of a single cell can be obtained via the Grid_getSingleCellVol or the Grid_getPointData routine. Use the Grid_getBlkData, Grid_getPlaneData, or Grid_getRowData routines with argument dataType=CELL_VOLUME To retrieve cell volumes for more than one cell of a block. To retrieve cell face areas, use the same Grid_get*Data interfaces with the appropriate dataType argument.
Note the following difference between the two groups of routines mentioned in
the previous two paragraphs: the routines for volumes and areas take
the chosen geometry into account in order to return geometric measures
of physical volumes and faces (or their RD equivalents).
On the other hand, the routines for coordinate values and widths
return values for ![]() ,
, ![]() , and
, and ![]() directly, without converting
angles to (arc) lengths.
directly, without converting
angles to (arc) lengths.
Currently, all of FLASH's physics support one-, two-, and
(with a few exceptions explicitly stated in the appropriate chapters) three-dimensional
Cartesian grids.
Some units, including the FLASH
Grid unit and PPM hydrodynamics unit (Chp:Hydrodynamics Unit),
support additional geometries, such as two-dimensional cylindrical (![]() ) grids,
one/two-dimensional spherical (
) grids,
one/two-dimensional spherical (![]() )/(
)/(![]() ) grids, and two-dimensional polar
(
) grids, and two-dimensional polar
(![]() ) grids. Some specific considerations for each geometry follow.
) grids. Some specific considerations for each geometry follow.
The following tables use the convention that
![]() and
and ![]() stand for the values of the
stand for the values of the ![]() coordinate at the “left” and
“right” end of the cell's
coordinate at the “left” and
“right” end of the cell's ![]() -coordinate range, respectively (i.e.,
-coordinate range, respectively (i.e.,
![]() is always true), and
is always true), and
![]() ; and similar for
the other coordinates.
; and similar for
the other coordinates.
FLASH uses Cartesian (plane-parallel) geometry by default. This is
equivalent to specifying
geometry = "cartesian"
Cell Volume in Cartesian Coordinates
|
To run FLASH with cylindrical coordinates, the geometry parameter must be set thus:
geometry = "cylindrical"
As in other non-Cartesian
geometries, if the minimum radius is chosen to be zero
(xmin = 0.), the left-hand boundary type should be reflecting
(or axisymmetric).
Of all supported non-Cartesian geometries, the cylindrical is
in 2-d most similar to a 2-d coordinate system: it uses two
linear coordinate axes (![]() and
and ![]() ) that form a rectangular
grid physically as well as logically.
) that form a rectangular
grid physically as well as logically.
As an illustrative example of the kinds of considerations
necessary in curved coordinates,
Figure 8.15 shows a jump in refinement along the cylindrical
`![]() ' direction. When performing the flux correction step at a jump
in refinement, we must take into account the area of the annulus
through which each flux passes to do the proper weighting. We
define the cross-sectional area through which the
' direction. When performing the flux correction step at a jump
in refinement, we must take into account the area of the annulus
through which each flux passes to do the proper weighting. We
define the cross-sectional area through which the ![]() -flux passes as
-flux passes as
| (8.99) |
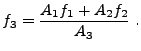 |
(8.100) |
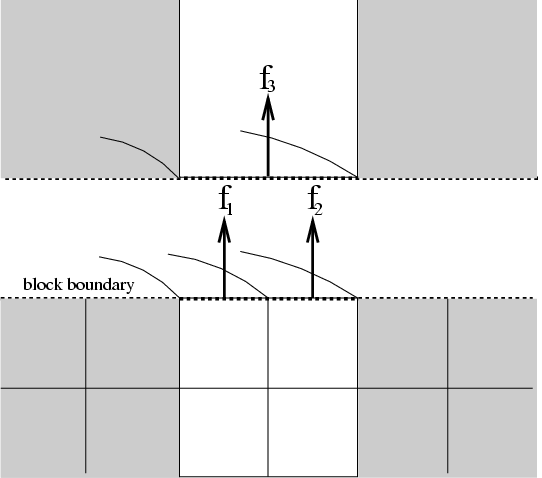
|
For fluxes in the radial direction, the cross-sectional area is independent
of the height, ![]() , so the corrected flux is simply taken as the average of
the flux densities in the adjacent finer cells.
, so the corrected flux is simply taken as the average of
the flux densities in the adjacent finer cells.
One or two dimensional spherical problems can be performed by
specifying
geometry = "spherical"
If the minimum radius is chosen to be zero (xmin = 0.), the left-hand boundary type should be reflecting.
geometry = "polar"
As in other non-Cartesian geometries, if the minimum radius is chosen to be zero (xmin = 0.), the left-hand boundary type should be reflecting.
When blocks are refined, we need to initialize the child data using the information in the parent cell in a manner which preserves the cell-averages in the coordinate system we are using. When a block is derefined, the parent block (which is now going to be a leaf block) needs to be filled using the data in the child blocks (which are soon to be destroyed). The first procedure is called prolongation. The latter is called restriction. Both of these procedures must respect the geometry in order to remain conservative. Prolongation and restriction are also used when filling guard cells at jumps in refinement.
These routines could be included by specifying the correct path in your Units file, or by using appropriate -unit= flags for setup. However, their use is not recommended.
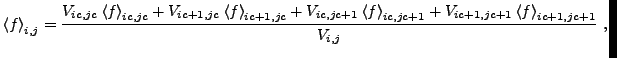 |
(8.101) |