31. X-ray Imaging Unit
The X-ray Imaging unit obtains an X-ray image of the domain at specific simulation
time(s) using the main driver function XrayImaging. The implementation
is based on sending one X-ray per detector screen resolution pixel through the domain and record
it's intensity reduction due to attenuation in the domain media. Currently only cold atomic
opacities are being used to determine the combined opacity of each cell's materials. Each detector
can record X-ray intensities for a mix of X-ray energies, thus each X-ray for each detector in the
code represents a bundle of X-rays with predefined distributions of X-ray energies. Each detector
is also given an X-ray point origin from which the X-rays originate.
31.0.1 X-ray Paths through Domain
All X-rays travel in straight lines through the domain. Each X-ray is given a dimensionless 3D unit
direction vector
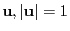 with components
with components
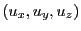 pointing from the detector
screen to its X-ray origin. Each direction vector component is a direct measure of how much
3D distance the X-ray travels between two such component points. For example, the direction vector
component
pointing from the detector
screen to its X-ray origin. Each direction vector component is a direct measure of how much
3D distance the X-ray travels between two such component points. For example, the direction vector
component 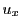 can be used to evaluate the 3D distance
can be used to evaluate the 3D distance 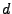 covered by the X-ray between two points
covered by the X-ray between two points
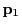 and
and 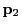 by using their components
by using their components 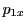 and
and 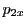 :
:
where, when removing the absolute value bars, we can judge, if the X-ray actually travelled that
distance (positive 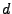 ) or not (negative
) or not (negative 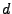 ), depending on the location of
), depending on the location of 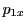 and
and 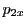 and the
sign of
and the
sign of 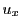 . For 3D cartesian domains it is therefore straighforward to find the minimum distance
travelled through a cell by chosing the minimum of all positive distances that are obtained from the
above Eq.(31.1) when replacing
. For 3D cartesian domains it is therefore straighforward to find the minimum distance
travelled through a cell by chosing the minimum of all positive distances that are obtained from the
above Eq.(31.1) when replacing 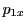 and
and 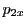 by the 3D cartesian cell
bounding box component pairs. Once
by the 3D cartesian cell
bounding box component pairs. Once 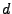 is found, we can use it to find the new X-ray's location
is found, we can use it to find the new X-ray's location
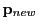 on the cell's bounding box from its old location
on the cell's bounding box from its old location
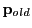 :
:
This simple procedure for 3D cartesian domian geometries changes for 3D X-ray tracing in 2D cylindrical
domain geometries. While the axial z-component is identical to the 3D cartesian case, the curved mantle
in the radial space makes it necessary to solve quadratic equations. Eq.(31.2)
can be seen as the parametric line equation of a 3D X-ray. We only look at the x- and y-components of the
line equation and add their squares together:
where
are the old and new radial 2D cylindrical positions of the 3D X-ray. The quadratic equation in 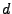 is solved
for positive
is solved
for positive 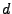 by inserting the 2D cylindrical cell radial bounding box pair
by inserting the 2D cylindrical cell radial bounding box pair
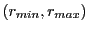 . Due to
the necessity of solving quadratics, the computational accuracy attainable for the radial
. Due to
the necessity of solving quadratics, the computational accuracy attainable for the radial 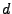 can be lower than
for the axial
can be lower than
for the axial 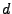 , which is solved by using the linear Eq.(31.1). Instead of forcing the
quadratic
, which is solved by using the linear Eq.(31.1). Instead of forcing the
quadratic 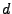 solution to be as accurate as the linear (axial)
solution to be as accurate as the linear (axial) 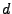 solution (for example by solving the
quadratic in higher precision), the linear X-ray propagation through the cell is allowed to take place using more
than one step (at most two steps are ever required). The 3D X-ray tracing in a 2D cylindrical domain also
requires constant adjustments between its 3D x- and y-position components and its 2D radial component, as for
example cell nudging of the X-ray must occur in the 2D cylindrical radial space. One cannot allow the
X-ray's x- and y-position components to get out of sync with the radial component, as all of them are needed to
solve Eq.(31.3).
solution (for example by solving the
quadratic in higher precision), the linear X-ray propagation through the cell is allowed to take place using more
than one step (at most two steps are ever required). The 3D X-ray tracing in a 2D cylindrical domain also
requires constant adjustments between its 3D x- and y-position components and its 2D radial component, as for
example cell nudging of the X-ray must occur in the 2D cylindrical radial space. One cannot allow the
X-ray's x- and y-position components to get out of sync with the radial component, as all of them are needed to
solve Eq.(31.3).
31.0.2 Creating and Tracing the X-rays
Each pixel center coordinate on the detector screen is the starting point of an X-ray. It's trajectory is
a straight line from the pixel center to the X-ray point origin of the detector screen. The X-ray's direction
vector 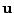 is pointing from the pixel center to the origin. Initial domain entry points for each
X-ray are determined using their
is pointing from the pixel center to the origin. Initial domain entry points for each
X-ray are determined using their 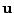 and Eq.(31.2), where
and Eq.(31.2), where
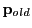 is the X-ray's global pixel center coordinates and
is the X-ray's global pixel center coordinates and
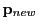 the domain boundaries. If an X-ray misses
the domain, it is recorded directly as a screen X-ray with zero attenuation. There is no screen miss possibility
for the X-ray, because per construction each X-ray belongs to a pixel on the detector screen. If the X-ray
hits the domain, its entry position and direction vector are stored to prepare for X-ray tracing through
the domain, as well as it's initital attenuation value is set to zero. Besides position, direction and
attenuation information, each domain X-ray needs additional data to help with its movement through the domain
and its transformation to a screen X-ray, such as current block and processor numbers, a global tag number
and the integer pixel pair label from where it originated on the detector screen. The screen X-rays will
only possess the local screen coordinate pair, it's calculated relative intensity in the range
the domain boundaries. If an X-ray misses
the domain, it is recorded directly as a screen X-ray with zero attenuation. There is no screen miss possibility
for the X-ray, because per construction each X-ray belongs to a pixel on the detector screen. If the X-ray
hits the domain, its entry position and direction vector are stored to prepare for X-ray tracing through
the domain, as well as it's initital attenuation value is set to zero. Besides position, direction and
attenuation information, each domain X-ray needs additional data to help with its movement through the domain
and its transformation to a screen X-ray, such as current block and processor numbers, a global tag number
and the integer pixel pair label from where it originated on the detector screen. The screen X-rays will
only possess the local screen coordinate pair, it's calculated relative intensity in the range ![$ [0,1]$](img1397.png) and
the detector screen number.
and
the detector screen number.
The mechanism for tracing the X-rays through the domain resembles the one used for tracing protons
through the domain. X-rays are created and traced through a frozen domain at a particular time step, hence
no time resolved X-ray tracing is needed. Batches of domain X-rays are generated and emptied into screen
X-ray buckets once the X-rays leave the domain. An important difference when compared to proton imaging is
that each batch of X-rays must correspond to one specific detector screen. The reason behind this is that
calculation of the cell opacities depends on the X-ray energies used and have to be calculated for each
detector separately. The X-ray energies hence influence the domain properties through material opacities,
whereas the proton energies only have an influence on their initial velocities and this property will not
change any domain values.
31.0.3 Setting up and Recording on the X-ray Detector Screens
The X-ray detector screens are identical in shape and specifications to the ones used for proton imaging
(see section 28.0.4). The same parameters are used to specify size (sidelength),
location (global position 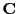 of the detector center) and orientation (screen normal vector
of the detector center) and orientation (screen normal vector 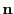 and tilting axis and angle) in space. Additional parameters used specifically for X-ray detectors are:
1) global origin
and tilting axis and angle) in space. Additional parameters used specifically for X-ray detectors are:
1) global origin 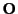 position as the source point for the X-rays, 2) activation time, indicating
the simulation time when the X-rays should be recorded, 3) screen resolution
position as the source point for the X-rays, 2) activation time, indicating
the simulation time when the X-rays should be recorded, 3) screen resolution 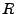 , which indicates how many
pixels will be along each detector side (leading to a total of
, which indicates how many
pixels will be along each detector side (leading to a total of 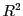 pixels), 4) the energy distribution
for each X-ray (finite set of X-ray energies and fractions of these X-ray energies adding up to 1) and
5) data related to each pixel size to facilitate recording of the X-rays on the screen. Recording the
X-rays on the detector screen is much simpler than for protons, since the target pixel is already known.
The X-rays integer pixel coordinate pair is converted to the local screen coordinate pair and the accumulated
attenuation
pixels), 4) the energy distribution
for each X-ray (finite set of X-ray energies and fractions of these X-ray energies adding up to 1) and
5) data related to each pixel size to facilitate recording of the X-rays on the screen. Recording the
X-rays on the detector screen is much simpler than for protons, since the target pixel is already known.
The X-rays integer pixel coordinate pair is converted to the local screen coordinate pair and the accumulated
attenuation 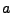 is translated to it's relative screen intensity
is translated to it's relative screen intensity 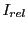 :
:
where 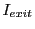 is the X-ray intensity when exiting the domain and
is the X-ray intensity when exiting the domain and 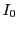 the initial X-ray intensity. Note,
that currently the initial intensity needs not be supplied as part of the detector info, since only relative
intensities are recorded. As for proton imaging, each X-ray detector file is set up as a formatted ascii file
with name:
the initial X-ray intensity. Note,
that currently the initial intensity needs not be supplied as part of the detector info, since only relative
intensities are recorded. As for proton imaging, each X-ray detector file is set up as a formatted ascii file
with name:
| |
|
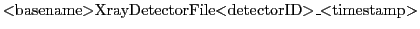 |
(31.7) |
where  basename
basename is the simulation name,
is the simulation name,  detectorID
detectorID is the detector number (currently
limited to the range [01-99]) and (optionally)
is the detector number (currently
limited to the range [01-99]) and (optionally)  timestamp
timestamp is the simulation time when the file was created.
Three quantities are written to the detector file for each X-ray: 1) the local screen coordinate pair
is the simulation time when the file was created.
Three quantities are written to the detector file for each X-ray: 1) the local screen coordinate pair
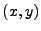 in the range
in the range ![$ [0,1]$](img1397.png) and 2) it's relative intensity
and 2) it's relative intensity 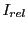 . Translation to a greyscale PGM picture
can be done by using the supplied ASCII
. Translation to a greyscale PGM picture
can be done by using the supplied ASCII  PGM greyscale converter software.
PGM greyscale converter software.
The following additions to the setup command activate the X-ray Imaging unit:
+XrayImaging [xray_maxDetectors=<number> threadXrayTrace=True]
- xray_maxDetectors: The maximum number of X-ray imaging detectors for the simulation (default = 1).
- xray_maxEnergyLevels: The maximum number of X-ray energy levels for a detector (default = 3).
- threadXrayTrace: Enables threading during X-ray domain tracing (default = false).
The following is a list of flash.par runtime parameters for the X-ray imaging unit.
The following are the runtime parameters for the X-ray imaging detectors. The _n at the
end of each runtime parameter characterizes the detector number and needs to be replaced by
_1 for the first detector, _n by _2 for the second detector, etc.
- xray_numberOfDetectors: The number of X-ray imaging detectors that are going to
be used.
- xray_detectorCenter[X,Y,Z]_n: The global 3D components of the detector center position
vector
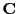 .
.
- xray_detectorOrigin[X,Y,Z]_n: The global 3D components of the X-rays origin position
vector
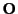 .
.
- xray_detectorNormal[X,Y,Z]_n: The local 3D components of the detector normal
vector
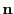 .
.
- xray_detectorEnergyLevelCount_n: The number of X-ray energy levels.
- xray_detectorEnergy_n_Level_i: The i-th X-ray energy level in eV. There must be
as many X-ray energy levels as the number of X-ray energy levels specified.
- xray_detectorEnergy_n_Fraction_i: The i-th X-ray energy level fraction contribution.
There must be as many X-ray energy level fractions as the number of X-ray energy levels specified.
All fractions must be in the range [0-1], and they must add up to 1.
- xray_detectorPerpXrays_n: If this parameter is set true, the origin X-ray position
will be ignored and all the X-rays will be hitting the screen in a perpendicular fashion, i.e. parallel
to the screen's normal direction vector. This is to avoid having to specify origin positions mimicking
an infinite distance away from the screen.
- xray_detectorResolution_n: The number of pixels along each side of the detector.
- xray_detectorSideLength_n: The side length (cm) of the detector square screen.
- xray_detectorSideTiltingAngle_n: The tilting angle (degrees) of two sides
parallel to the detector screen unit axis
![$ {\bf u}_y]$](img2677.png) with respect to the tilting axis.
with respect to the tilting axis.
- xray_detectorSideTiltingAxis_n: The global tilting axis ('x','y' or 'z')
for the detector screen.
- xray_detectorAlignWRTorigin_n: A useful shortcut to orient the detector
screen in such a way that the normal vector coincides with the origin / detector center line.
Given the origin
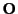 and the detector center
and the detector center 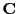 , the normal vector
, the normal vector 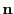 is
recalculated such that
is
recalculated such that
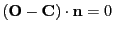 .
.
- xray_cellWallThicknessFactor: Controls the (imaginary) thickness of the cell
walls to ensure computational stability of the X-ray imaging code. The cell thickness is defined as this
factor times the smallest cell dimension along all geometrical axes. The factor is currently
set to
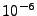 and should only very rarely be changed.
and should only very rarely be changed.
- xray_3Din2D: Indicates, whether this is a 3D X-ray in 2D cylindrical domain
simulation.
- xray_detectorFileNameTimeStamp: If set to true, a time stamp will be added to
each detector file name. This allows for time splitting of detectors.
- xray_detectorXYwriteFormat: Controls formatted ascii output of the screen
X-ray local coordinate
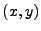 pairs on the detector screens (default 'es20.10').
pairs on the detector screens (default 'es20.10').
- xray_detectorDGwriteFormat: Controls formatted ascii output of the screen X-ray
relative intensities
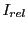 on the detector screens (default 'es15.5').
on the detector screens (default 'es15.5').
- xray_maxXrayCount: The maximum number of X-rays that can be created on one processor
per batch in the domain.
- xray_printDetectors: If true, it prints detailed information about the X-ray
detectors to a file with name
 basename
basename XrayImagingDetectors.txt, where
XrayImagingDetectors.txt, where  basename
basename is
the base name of the simulation.
is
the base name of the simulation.
- xray_printMain: If true, it prints general information regarding the X-ray
imaging setup to a file with name
 basename
basename XrayImagingMainPrint.txt, where
XrayImagingMainPrint.txt, where  basename
basename is the base name of the simulation.
is the base name of the simulation.
- xray_printSpecies: If true, it prints general information regarding the all
the species present in the current simulation to a file named
 basename
basename XrayImagingMainSpecies.txt,
where
XrayImagingMainSpecies.txt,
where  basename
basename is the base name of the simulation. It records the atomic element decomposition
of each species with number and mass fractions and also records the cold opacities of each species
for each detector (depending on the X-ray energy specified).
is the base name of the simulation. It records the atomic element decomposition
of each species with number and mass fractions and also records the cold opacities of each species
for each detector (depending on the X-ray energy specified).
- xray_printXrays: If true, it activates printout of domain X-ray data at specific
stages during the domain X-ray tracing. This runtime parameter is meant solely for debugging purposes
and calls to the corresponding X-ray printing routine can be placed anywhere in the X-ray imaging code.
Each processor writes its own file(s) with name(s):

basename

printXraysDetBatch

DetectorBatchNr

Proc

ProcessorID

_

simulationTime

.txt,
where  basename
basename is the base name of the simulation. An optional _Tag
is the base name of the simulation. An optional _Tag Tagnumber
Tagnumber can be added
to these files to distinguish between printouts at different strategic places. Use of this feature
is reserved ONLY for debugging purposes and is currently limited to 1000 detector batches and 1000
processors per time stamp. Users other than code developers should not activate this feature.
can be added
to these files to distinguish between printouts at different strategic places. Use of this feature
is reserved ONLY for debugging purposes and is currently limited to 1000 detector batches and 1000
processors per time stamp. Users other than code developers should not activate this feature.
- xray_XrayDeterminism: If true, the Grid Unit will be forced to use the sieve
algorithm to move the X-ray particle data. Forcing this algorithm will result in a slower movement
of data, but will fix the order the processors pass data and eliminate round off differences in
consecutive runs.
- xray_screenXrayBucketSize: Sets the bucket size for flushing screen X-rays out to disk.
- useXrayImaging: If false, no X-ray imaging will be performed,
even if the code was compiled to do so. Bypasses the need to rebuild the code.
- threadXrayTrace: If true, X-ray tracing through a block is threaded. This runtime
parameter can only be set during setup of the code.
The unit test supplied for the X-ray imaging unit is based on putting a sphere of pure iron inside
a domain filled with pure hydrogen. The hydrogen opacity is enforced to be equal to zero, hence
attenuation of the X-rays is solely due to the atomic opacity of iron in the sphere. For each type
of domain (3D cartesian and 2D cylindrical), three detector screens, each with resolution R = 1000, are
placed at three different positions in space. For the cubic 3D cartesian domain, the three screen
positions are along a face center, edge center and vertex direction. For the 2D cylindrical domain,
we also place the three screens along the radial, axial and cylinder edge of the implied 3D cylinder.
Attenuation of the X-rays are recorded and compared to analytically obtained bounds.
Given a sphere with radius 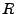 and located with its center at
and located with its center at 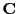 , any X-ray with screen location
, any X-ray with screen location
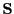 and origin location
and origin location 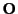 will travel a distance
will travel a distance 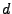 inside the sphere given by:
inside the sphere given by:
where  is the distance between
is the distance between 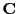 and
and 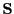 and
and 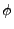 is the angle between the
vectors
is the angle between the
vectors
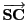 and
and
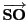 . The sphere representation inside
the domain is blocky in all three directions for 3D cartesian domains and blocky in the axial direction
(stacked cylindrical disks) for 2D cylindrical domains. Hence Eq.(31.8) cannot
be directly used to determine the exact distance travelled through the blocky spheres. However, one
can define two extra spheres: 1) Maximum inner sphere, with radius
. The sphere representation inside
the domain is blocky in all three directions for 3D cartesian domains and blocky in the axial direction
(stacked cylindrical disks) for 2D cylindrical domains. Hence Eq.(31.8) cannot
be directly used to determine the exact distance travelled through the blocky spheres. However, one
can define two extra spheres: 1) Maximum inner sphere, with radius 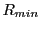 , which is the largest
sphere that can be placed completely inside the blocky spheres and 2) Minimum outer sphere, with radius
, which is the largest
sphere that can be placed completely inside the blocky spheres and 2) Minimum outer sphere, with radius
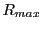 , which is the smallest sphere that can contains the blocky spheres completely. Since the
positions of the X-ray don't change,
, which is the smallest sphere that can contains the blocky spheres completely. Since the
positions of the X-ray don't change, 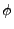 and
and  does not change and each
does not change and each 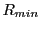 and
and 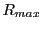 also define through Eq.(31.8) corresponding X-ray distances
also define through Eq.(31.8) corresponding X-ray distances 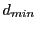 and
and
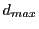 travelled through the maximum inner and minimum outer spheres. We then have the following
three inequalities
travelled through the maximum inner and minimum outer spheres. We then have the following
three inequalities
where 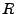 ,
,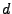 and X-ray intensity
and X-ray intensity 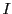 correspond to the blocky sphere quantities. Using
correspond to the blocky sphere quantities. Using 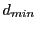 and
and 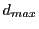 ,
upper and lower bounds for the X-ray attenuation can be given when crossing the domain, leading to X-ray
intensities
,
upper and lower bounds for the X-ray attenuation can be given when crossing the domain, leading to X-ray
intensities 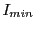 and
and 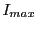 due to the maximum inner and minimum outer spheres.
due to the maximum inner and minimum outer spheres.
For the 3D cartesian unit test, we set up a cubic box with side length 10 cm. A pure iron sphere with
density 0.3 g/cm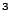 and radius 5 cm is created at the center of the domain, using uniform refinement
level 6 for the AMR grid. Detector screens with resolution R = 1000 and of side length 25 cm are
placed at the following 3 different places, such that the sphere center and the detector screen centers
are 10 cm apart: 1) along the y face center direction (0,1,0), along the edge center direction (1,1,0)
and along the vertex direction (1,1,1). The corresponding X-ray origins are all placed in the opposite
directions with origin / screen center distance of 20 cm. All X-ray energies are set to 60 keV.
The three intensities
and radius 5 cm is created at the center of the domain, using uniform refinement
level 6 for the AMR grid. Detector screens with resolution R = 1000 and of side length 25 cm are
placed at the following 3 different places, such that the sphere center and the detector screen centers
are 10 cm apart: 1) along the y face center direction (0,1,0), along the edge center direction (1,1,0)
and along the vertex direction (1,1,1). The corresponding X-ray origins are all placed in the opposite
directions with origin / screen center distance of 20 cm. All X-ray energies are set to 60 keV.
The three intensities 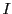 ,
, 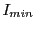 ,
, 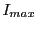 of each X-ray from all three detectors are analyzed and
the unit test is marked successful, if for all X-rays the intensity inequality in
Eq.(31.9) is fulfilled.
of each X-ray from all three detectors are analyzed and
the unit test is marked successful, if for all X-rays the intensity inequality in
Eq.(31.9) is fulfilled.
The 2D cylindrical unit test is set up to match the 3D cartesian one. The 2D cylindrical domain has
an axial dimension of 10 cm and a radius dimension of 5 cm. The implicit 3D sphere is placed in form of
a semicircle with center at the domain location (radial,axial) = (0,5). All other sphere specifications
(material and density) and detector specifications (side length 25 cm, R = 1000, detector center to
detector origin distance = 20 cm, detector center to sphere center distance = 10cm) match the 3D
cartesian unit test. The three detectors are placed as follows: 1) along the axial
direction, 2) along the radial direction and 3) along the cylindrical edge direction. The 2D cylindrical
unit test is successful, if all X-ray intensities are within the bounds mentioned previously.
Subsections
![]() with components
with components
![]() pointing from the detector
screen to its X-ray origin. Each direction vector component is a direct measure of how much
3D distance the X-ray travels between two such component points. For example, the direction vector
component
pointing from the detector
screen to its X-ray origin. Each direction vector component is a direct measure of how much
3D distance the X-ray travels between two such component points. For example, the direction vector
component ![]() can be used to evaluate the 3D distance
can be used to evaluate the 3D distance ![]() covered by the X-ray between two points
covered by the X-ray between two points
![]() and
and ![]() by using their components
by using their components ![]() and
and ![]() :
:
![]() is pointing from the pixel center to the origin. Initial domain entry points for each
X-ray are determined using their
is pointing from the pixel center to the origin. Initial domain entry points for each
X-ray are determined using their ![]() and Eq.(31.2), where
and Eq.(31.2), where
![]() is the X-ray's global pixel center coordinates and
is the X-ray's global pixel center coordinates and
![]() the domain boundaries. If an X-ray misses
the domain, it is recorded directly as a screen X-ray with zero attenuation. There is no screen miss possibility
for the X-ray, because per construction each X-ray belongs to a pixel on the detector screen. If the X-ray
hits the domain, its entry position and direction vector are stored to prepare for X-ray tracing through
the domain, as well as it's initital attenuation value is set to zero. Besides position, direction and
attenuation information, each domain X-ray needs additional data to help with its movement through the domain
and its transformation to a screen X-ray, such as current block and processor numbers, a global tag number
and the integer pixel pair label from where it originated on the detector screen. The screen X-rays will
only possess the local screen coordinate pair, it's calculated relative intensity in the range
the domain boundaries. If an X-ray misses
the domain, it is recorded directly as a screen X-ray with zero attenuation. There is no screen miss possibility
for the X-ray, because per construction each X-ray belongs to a pixel on the detector screen. If the X-ray
hits the domain, its entry position and direction vector are stored to prepare for X-ray tracing through
the domain, as well as it's initital attenuation value is set to zero. Besides position, direction and
attenuation information, each domain X-ray needs additional data to help with its movement through the domain
and its transformation to a screen X-ray, such as current block and processor numbers, a global tag number
and the integer pixel pair label from where it originated on the detector screen. The screen X-rays will
only possess the local screen coordinate pair, it's calculated relative intensity in the range ![]() and
the detector screen number.
and
the detector screen number.
![]() of the detector center) and orientation (screen normal vector
of the detector center) and orientation (screen normal vector ![]() and tilting axis and angle) in space. Additional parameters used specifically for X-ray detectors are:
1) global origin
and tilting axis and angle) in space. Additional parameters used specifically for X-ray detectors are:
1) global origin ![]() position as the source point for the X-rays, 2) activation time, indicating
the simulation time when the X-rays should be recorded, 3) screen resolution
position as the source point for the X-rays, 2) activation time, indicating
the simulation time when the X-rays should be recorded, 3) screen resolution ![]() , which indicates how many
pixels will be along each detector side (leading to a total of
, which indicates how many
pixels will be along each detector side (leading to a total of ![]() pixels), 4) the energy distribution
for each X-ray (finite set of X-ray energies and fractions of these X-ray energies adding up to 1) and
5) data related to each pixel size to facilitate recording of the X-rays on the screen. Recording the
X-rays on the detector screen is much simpler than for protons, since the target pixel is already known.
The X-rays integer pixel coordinate pair is converted to the local screen coordinate pair and the accumulated
attenuation
pixels), 4) the energy distribution
for each X-ray (finite set of X-ray energies and fractions of these X-ray energies adding up to 1) and
5) data related to each pixel size to facilitate recording of the X-rays on the screen. Recording the
X-rays on the detector screen is much simpler than for protons, since the target pixel is already known.
The X-rays integer pixel coordinate pair is converted to the local screen coordinate pair and the accumulated
attenuation ![]() is translated to it's relative screen intensity
is translated to it's relative screen intensity ![]() :
:
![]() and located with its center at
and located with its center at ![]() , any X-ray with screen location
, any X-ray with screen location
![]() and origin location
and origin location ![]() will travel a distance
will travel a distance ![]() inside the sphere given by:
inside the sphere given by:
![]() and radius 5 cm is created at the center of the domain, using uniform refinement
level 6 for the AMR grid. Detector screens with resolution R = 1000 and of side length 25 cm are
placed at the following 3 different places, such that the sphere center and the detector screen centers
are 10 cm apart: 1) along the y face center direction (0,1,0), along the edge center direction (1,1,0)
and along the vertex direction (1,1,1). The corresponding X-ray origins are all placed in the opposite
directions with origin / screen center distance of 20 cm. All X-ray energies are set to 60 keV.
The three intensities
and radius 5 cm is created at the center of the domain, using uniform refinement
level 6 for the AMR grid. Detector screens with resolution R = 1000 and of side length 25 cm are
placed at the following 3 different places, such that the sphere center and the detector screen centers
are 10 cm apart: 1) along the y face center direction (0,1,0), along the edge center direction (1,1,0)
and along the vertex direction (1,1,1). The corresponding X-ray origins are all placed in the opposite
directions with origin / screen center distance of 20 cm. All X-ray energies are set to 60 keV.
The three intensities ![]() ,
, ![]() ,
, ![]() of each X-ray from all three detectors are analyzed and
the unit test is marked successful, if for all X-rays the intensity inequality in
Eq.(31.9) is fulfilled.
of each X-ray from all three detectors are analyzed and
the unit test is marked successful, if for all X-rays the intensity inequality in
Eq.(31.9) is fulfilled.