Subsections
As of FLASH4.5, we provide the a “Simple” implementation of Thomson Scattering.
In the future, an implementation that employs true ray tracing may be provided.
In the “simple” implementation, We do not “trace” rays but “cast” them: “rays” consist
of two straight-line parts, which we'll refer to as “leg 1” and “leg 2”.
The power deposited in an experiment by a probe laser may significantly alter
the behavior of the physical system, by deposition energy into the system.
This is usually an undesired effect.
The ThomsonScattering unit does not model this effect.
As a purely diagnostic unit, it has no impact on the dynamics
of the physical system.
However, a ThomsonScattering configuration can easily be combined
with a configuration of a laser for energy deposition, provided by
the EnergyDeposition unit, see Sec:EnergyDeposition.
Commonly this configuration will consist of adding a laser beam,
in addition to the beams already present in an experimental setup.
The definitions of pulse, beam parameters, etc., for this additional
beams should closely mirror the runtime parameters chosen to configure the
Thomson probe laser beam.
The ThomsonScattering unit will fill several variables with
information about the Thomson probe laser power and its spatial
distribution, if variables of the following names are defined:
- pwin - Power in, restricted to a “measurement region” that is used to
calibrate the configured laser power.
- pwia - Power in, everywhere except in locations that are forbidden
because the cirtical electron density is exceeded.
- pwi1 - Power in, with leg 1 attenuation applied, computed everywhere
in the domain.
Note that this can increase run time very significantly, since
integrations along many more ray paths have to be performed than what
is needed for computing scattering spectra.
- pwi2 - Power in, with leg 1 and leg 2 attenuation applied.
Only computed in regions within the cone defined by a detector's
opening angle.
- pwde - Total power of detectable scattered light, without attenuation.
- pwi1 - Total power of detectable scattered light, with leg 1 attenuation applied.
- pwi2 - Total power of detectable scattered light, with leg 1 and leg 2 attenuation applied.
Laser Energy Density for the probe laser can be made available for
visualization in the lase variable, if an EnergyDeposition
beam has been added to the configuration, es described in Sec:LASE.
As mentioned above, we provide the a “Simple” implementation of Thomson Scattering.
Even though the code uses “raytracing” terminology in some variable names etc.,
realy we are “casting” rays along predetermined paths, rather than letting each
ray find its own path through set-by-step integration.
30.2.5 Setting up the Probe Laser Pulse
We use runtime parameters analogous to those of the EnergyDeposition unit to
configure the time behavior of the ThomsonScattering unit. Computations are only
performed by this code unit at times when the probe laser pulse is nonzero.
Additionally, a time-dependent probe laser power will directly affect the absolute scaling of
computed spectro, so it can be useful for comparing a sequence of spectra computed
at different times.
The laser's pulse contains information about the laser's energy profile and can thus be characterized by a
function of laser power in terms of time 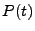 . The curve of
. The curve of 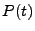 gives the power of the laser pulse
at any given simulation time. In FLASH, the form of
gives the power of the laser pulse
at any given simulation time. In FLASH, the form of 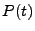 is given by a series of points, which are
connected via straight lines (see Figure 18.5).
is given by a series of points, which are
connected via straight lines (see Figure 18.5).
Note, that 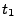 is the time the laser first comes
into existence. In Figure 18.5 there is therefore no line connecting the origin (zero power)
with
is the time the laser first comes
into existence. In Figure 18.5 there is therefore no line connecting the origin (zero power)
with 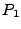 . If the user wants a gradual buildup of laser power from zero, an explicit point
. If the user wants a gradual buildup of laser power from zero, an explicit point 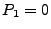 must be given at time
must be given at time 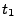 . The same consideration applies for the other end of the timescale.
. The same consideration applies for the other end of the timescale.
Runtime parameters thsc_spectrumFileIntervalStep and
thsc_spectrumFileIntervalTime can be used to limit
the frequency of scattering computations, so that they won't happen at the end of
every time step wile the probe laser is on.
30.2.6 Setting up the Laser Beam
Note: currently only one probe beam is supported.
The setup of each laser beam follows closely the setup of the laser beams in 18.4.6
for energy-depositing lasers.
While the implementation of rays is quite different, we aim to make setting up a Thomson scattering probe
laser beam very simir to setting up a beam for laser energy deposition.
Lens and arget coordinates are used for directing a beam.
Additional runtime parameters needed for each beam are: 1) the launching time (the beam
fires once the simulation time exceeds the launching time), 2) its target detector screen and 3) the beam power.
For the ThomsonScattering unit, lens and target ellipses can both be fully or partially inside or
outside the simulation volume.
30.2.7 Creating the Rays
The rays inside each beam are created by connecting one-to-one
grid points inside the
lens area with the subcell center points inside the interaction region. The ray directions inside
each beam can be parallel or conically diverging or converging collinear and are not allowed to cross. The lens positions and
directions at the lens are calculated using the same strategy as presented in
18.4.7.6. Rays missing the domain can either be simply ignored or directly
recorded on the detector screen.
30.2.7.1 Ray Specifications
Each beam/disk ray needs to know its position 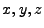 and velocity
and velocity
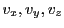 as it traverses the domain.
In addition to these 6 components it needs to know: 1) the time spent travelling in domain, 2) the current
block and processor numbers, 3) a global identification tag, 4) the originating beam and target detector numbers.
Screen rays on the other hand are only defined on the detector screen and hence need no specific information
for domain travelling. Their information is reduced to a screen position coordinate pair
as it traverses the domain.
In addition to these 6 components it needs to know: 1) the time spent travelling in domain, 2) the current
block and processor numbers, 3) a global identification tag, 4) the originating beam and target detector numbers.
Screen rays on the other hand are only defined on the detector screen and hence need no specific information
for domain travelling. Their information is reduced to a screen position coordinate pair 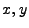 and a detector number
to which detector they are associated with.
and a detector number
to which detector they are associated with.
Additionally, upon request, the Thomson scattering code is able to calculate extra magnetic diagnostic
quantities 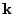 and
and 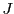 for each beam/disk and screen ray:
for each beam/disk and screen ray:
where
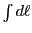 denotes path integration,
denotes path integration, 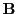 is the magnetic field vector and
is the magnetic field vector and
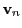 is the unit normal velocity vector along the ray path. Transforming the path integrals into
time integrals using the relation
is the unit normal velocity vector along the ray path. Transforming the path integrals into
time integrals using the relation
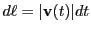 , we get the differentials:
, we get the differentials:
30.2.8 Setting up the Detectors
Note: currently only one detector is supported.
Each detector is defined as a point together with a cone of directions from which it can receive
light, the latter defined by a direction and an opening angle.
Thus the geometry is specified by three components:
1) the detector location 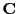 , 2) the unit vector
, 2) the unit vector 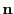 of the direction of the cone axis,
and 3) the angle
of the direction of the cone axis,
and 3) the angle 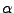 .
.
30.2.8.1 Recording Rays at the Detector
Each ray that reaches the detector gets recorded. Two kinds of files can be generated at the
end of ThomsonScattering processing:
- a detector file, and/or
- a spectrum file.
Runtime parameters thsc_spectrumFileIntervalStep and
thsc_spectrumFileIntervalTime determine approximately how
often these files are generated. This is only approximate because these
runtime parameters do not modify the simulation time step.
Currenly, generation of one kind of these files may force generation of the other one
at the same time. Each detector file is currently an ascii file (formatted) and named:
| |
|
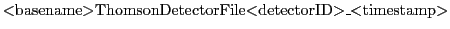 |
(30.12) |
where  basename
basename is the name of the simulation,
is the name of the simulation,  detectorID
detectorID is the detector number (currently
limited to the range [01-99]) and (optionally)
is the detector number (currently
limited to the range [01-99]) and (optionally)  timestamp
timestamp is the simulation time when the file was created.
Only the
is the simulation time when the file was created.
Only the 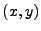 pairs are written (first
pairs are written (first  followed by
followed by  on each line) without any headers. Thus the file
can be directly incorporated and read by other software for graphical output (see for example the proton
imaging ASCII
on each line) without any headers. Thus the file
can be directly incorporated and read by other software for graphical output (see for example the proton
imaging ASCII  PGM greyscale converter). Each spectrum file is also a text file and named:
PGM greyscale converter). Each spectrum file is also a text file and named:
| |
|
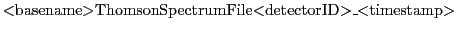 |
(30.13) |
where  basename
basename is the name of the simulation,
is the name of the simulation,  detectorID
detectorID is the detector number (currently
limited to the range [01-99]) and (optionally)
is the detector number (currently
limited to the range [01-99]) and (optionally)  timestamp
timestamp is the simulation time when the file was created.
The first two columns are wave length and detected intensity, respectively. There will normally be
thsc_spectrumNpts_N lines.
is the simulation time when the file was created.
The first two columns are wave length and detected intensity, respectively. There will normally be
thsc_spectrumNpts_N lines.
To include the use of the Thomson Scattering unit, something like the following can be included into the
setup command line:
-unit=diagnostics/ThomsonScattering [thsc_maxBeams=<number> thsc_maxDetectors=<number> threadThomsonSc=True]
- thsc_maxBeams: The maximum number ray beams for the simulation.
- thsc_maxDetectors: The maximum number of Thomson scattering detectors for the simulation.
- threadThomsonSc: Enables threading during ray domain tracing.
Using Thomson scattering runtime parameters in the flash.par file, the user can set up the proper ray
imaging configuration for his specific needs. The following list of runtime parameters is
currently available for the user.
The following are some runtime parameters for the Thomson scattering beams. The _n at the end of each
runtime parameter characterizes the beam number, hence replace _n by _1 for the first beam,
_n by _2 for the second beam, etc.
See Beam Runtime Parameters for a more complete list of beam parameters.
- thsc_numberOfBeams: The number of Thomson scattering beams that are going to be used.
- thsc_beamLens[X,Y,Z]_n: The global 3D components of the lens center position vector
 .
.
- thsc_beamTarget[X,Y,Z]_n: The global 3D components of the target position
vector
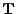 .
.
- thsc_beamDetector_n: The detector number, where the rays of the beam
should be recorded. This should be set to 1 as long as only one detector is used.
- thsc_maxRayCount: Maximum total number of rays. Rays may be dropped if this
number is exceeded.
Note: only configurations with one beam have been tested as of FLASH4.5.
The following are some runtime parameters for the Thomson scattering detectors. In most of them, the _n at the
end of each runtime parameter characterizes the detector number, usually “1”.
See Detector Runtime Parameters for a more complete list of detector parameters.
Note: currently only one detector is supported.
- thsc_detectorFileNameTimeStamp: If set to true, a time stamp will be added to
each detector file name. This allows for time splitting of detectors.
- thsc_detectorXYwriteFormat: Controls formatted ascii output of the ray
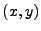 pairs on the detector screens (default 'es20.10').
pairs on the detector screens (default 'es20.10').
- thsc_detectorDGwriteFormat: Controls formatted ascii output of the magnetic
diagnostic quantities
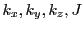 on the detector screens (default 'es15.5').
on the detector screens (default 'es15.5').
- thsc_maxRayCount: The maximum number of beam/disk rays that can be
created/read-in on one processor per batch in the domain.
- thsc_printPulses: If true, it prints detailed information about the laser
pulses to a file with name
 basename
basename ThomsonPulsesPrint.txt, where
ThomsonPulsesPrint.txt, where  basename
basename is the base
name of the simulation.
is the base
name of the simulation.
- thsc_printBeams: If true, it prints detailed information about the ray
beams to a file with name
 basename
basename ThomsonBeamsPrint.txt, where
ThomsonBeamsPrint.txt, where  basename
basename is
the base name of the simulation.
is
the base name of the simulation.
- thsc_printDetectors: If true, it prints detailed information about the ray
detectors to a file with name
 basename
basename ThomsonDetectorsPrint.txt, where
ThomsonDetectorsPrint.txt, where  basename
basename is
the base name of the simulation.
is
the base name of the simulation.
- thsc_printMain: If true, it prints general information regarding the ray
imaging setup to a file with name
 basename
basename ThomsonScatteringMainPrint.txt, where
ThomsonScatteringMainPrint.txt, where  basename
basename is the base name of the simulation.
is the base name of the simulation.
- thsc_recordOffScreenRays: If true, rays not hitting their target detector screen
are also recorded on the detector files. These rays will have screen coordinate pairs
![$ (x,y)\notin [0,1]$](img2672.png) .
.
- thsc_screenRayBucketSize: Sets the bucket size for flushing screen rays
out to disk.
- thsc_screenRayDiagnostics: If true, the magnetic diagnostic quantities
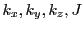 are evaluated for each ray and recorded on the detector screens.
are evaluated for each ray and recorded on the detector screens.
- useThomsonScattering: If false, no Thomson scattering will be performed,
even if the code was compiled to do so. Bypasses the need to rebuild the code.
A version of the laser Slab setup with an added Thomson scattering diagnostic is provided,
see Sec:LaserSlabThc for a description.
![]() . The curve of
. The curve of ![]() gives the power of the laser pulse
at any given simulation time. In FLASH, the form of
gives the power of the laser pulse
at any given simulation time. In FLASH, the form of ![]() is given by a series of points, which are
connected via straight lines (see Figure 18.5).
is given by a series of points, which are
connected via straight lines (see Figure 18.5).
![]() is the time the laser first comes
into existence. In Figure 18.5 there is therefore no line connecting the origin (zero power)
with
is the time the laser first comes
into existence. In Figure 18.5 there is therefore no line connecting the origin (zero power)
with ![]() . If the user wants a gradual buildup of laser power from zero, an explicit point
. If the user wants a gradual buildup of laser power from zero, an explicit point ![]() must be given at time
must be given at time ![]() . The same consideration applies for the other end of the timescale.
. The same consideration applies for the other end of the timescale.
![]() and velocity
and velocity
![]() as it traverses the domain.
In addition to these 6 components it needs to know: 1) the time spent travelling in domain, 2) the current
block and processor numbers, 3) a global identification tag, 4) the originating beam and target detector numbers.
Screen rays on the other hand are only defined on the detector screen and hence need no specific information
for domain travelling. Their information is reduced to a screen position coordinate pair
as it traverses the domain.
In addition to these 6 components it needs to know: 1) the time spent travelling in domain, 2) the current
block and processor numbers, 3) a global identification tag, 4) the originating beam and target detector numbers.
Screen rays on the other hand are only defined on the detector screen and hence need no specific information
for domain travelling. Their information is reduced to a screen position coordinate pair ![]() and a detector number
to which detector they are associated with.
and a detector number
to which detector they are associated with.
![]() and
and ![]() for each beam/disk and screen ray:
for each beam/disk and screen ray:
![]() , 2) the unit vector
, 2) the unit vector ![]() of the direction of the cone axis,
and 3) the angle
of the direction of the cone axis,
and 3) the angle ![]() .
.