Subsections
7.1 Driver Routines
The most important routines in the Driver API are those that initialize,
evolve, and finalize the FLASH program.
The file
Flash.F90
contains the main FLASH program (equivalent to main() in C).
The default top-level program of FLASH,
Simulation/Flash.F90, calls Driver routines in this order:
program Flash
implicit none
call Driver_initParallel()
call Driver_initFlash()
call Driver_evolveFlash( )
call Driver_finalizeFlash ( )
end program Flash
Therefore the no-operation stubs for these routines in the Driver source directory
must be overridden by an implementation function in a unit implementation directory under the Driver
or Simulation directory trees,
in order for
a simulation to perform any meaningful actions.
The most commonly used implementations
for most of these files are located in the
Driver/DriverMain unit implementation directory, with
a few specialized ones in either
Driver/DriverMain/Split or
Driver/DriverMain/Unsplit.
The first of these routines is Driver_initParallel, which
initializes the parallel environment for the simulation. New in
FLASH4 is an ability to replicate the mesh where more than one
copy of the discretized mesh may exist with some overlapping and some
non-overlapping variables. Because of this feature, the
parallel environment differentiates between global and mesh
communicators. All the necessary communicators, and the attendant
meta-data is generated in this routine. Also because of this
modification, runtime parameters such as iProcs, jProcs etc, which
were under the control of the Grid unit in FLASH3, are now under
the control of the Driver unit. Several new accessor interface
allow other code units to query the driver unit for this information.
The Driver_initFlash, the next routine, in general calls the
initialization routines in each of the units. If a unit is not
included in a simulation, its stub (or empty) implementation is
called. Having stub implementations is very useful in
the Driver unit because it allows the user to avoid writing a new driver
for each simulation. For a more detailed explanation of stub implementations please see Sec:Unit Architecture.
It is important to note that when individual units are being
initialized, order is often very important and the order of initialization is different depending
on whether the run is from scratch or being restarted from a checkpoint file.
The next routine is Driver_evolveFlash which controls
the timestepping of the simulation, as well as the normal termination of FLASH
based on time. Driver_evolveFlash checks the parameters tmax,
nend and zFinal to determine that the run should end, having
reached a particular point in time, a certain number of steps, or a particular
cosmological redshift, respectively. Likewise the initial simulation time,
step number and cosmological redshift for a simulation can be set using
the runtime parameters tmin, nbegin, and zInitial.
This version of FLASH includes versions of Driver_evolveFlash for
directionally-split and unsplit staggered mesh operators.
The code in the Driver/DriverMain/Split unit implementation directory has been the default
time update method up to FLASH4.3, and can still be be used for
many setups that can be configured with
FLASH. The routine Driver_evolveFlash implements a
Strang-split method of time advancement where each physics unit
updates the solution data for two equal timesteps - thus the sequence
of calls to physics and other units in each time step goes something like this:
Hydro, diffusive terms, source terms, Particles, Gravity;
Hydro, diffusive terms, source terms, Particles, Gravity,
IO (for output), Grid (for grid changes).
The
hydrodynamics update routines take a “sweep order” argument since
they must be directionally split to work with this driver. Here, the
first call usually uses the ordering 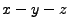 , and the second call uses
, and the second call uses
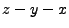 . Each of the update routines is assumed to directly modify the
solution variables. At the end of one loop of timestep advancement,
the condition for updating the mesh refinement pattern is tested if
the adaptive mesh is being used, and a refinement update is carried
out if required.
. Each of the update routines is assumed to directly modify the
solution variables. At the end of one loop of timestep advancement,
the condition for updating the mesh refinement pattern is tested if
the adaptive mesh is being used, and a refinement update is carried
out if required.
The driver implementation in the Driver/DriverMain/Unsplit directory is
the default since FLASH4.4.
It is required
specifically for the two unsplit solvers:
unsplit staggered mesh MHD solver (Sec:usm_algorithm) and the unsplit
gas hydrodynamics solver (Sec:unsplit hydro algorithm).
This implementation in general calls each of the physics routines only once
per time step, and
each call advances solution vectors by one timestep.
At the end of one loop of timestep advancement, the condition for updating the
adaptive mesh refinement pattern is tested and applied.
A new timestepping method implemented in FLASH4 is a technique called
Super-Time-Stepping (STS). The STS is a simple explicit method which is
used to accelerate restrictive parabolic timestepping advancements (
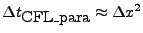 )
by relaxing the CFL stability condition of parabolic equation system.
)
by relaxing the CFL stability condition of parabolic equation system.
The STS has been proposed by Alexiades et al., (1996), and used in computational astrophysics and sciences recenly
(see Mignone et al., 2007; O'Sullivan & Downes, 2006; Commerçon et al., 2011; Lee, D. et al, 2011)
for solving systems of parabolic PDEs numerically. The method increases its effective time steps
 using two properties of stability and optimality in
Chebychev polynomial of degree
using two properties of stability and optimality in
Chebychev polynomial of degree 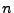 . These properties optimally
maximize the time step
. These properties optimally
maximize the time step
 by which a solution vector can be
evolved. A stability condition is imposed only after each time
step
by which a solution vector can be
evolved. A stability condition is imposed only after each time
step
 , which is further subdivided into smaller
, which is further subdivided into smaller
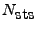 sub-time steps,
sub-time steps, 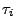 , that is,
, that is,
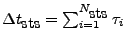 , where
the sub-time step is given by
, where
the sub-time step is given by
![$\displaystyle \tau_i=\Delta t_{\mbox{CFL\_para}}\big[ (-1+\nu_{\mbox{sts}}) cos\big(\frac{\pi(2j-1)}{2N_{\mbox{sts}}} + 1+\nu_{\mbox{sts}} \big)\big]^{-1},$](img150.png) |
(7.1) |
where
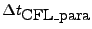 is an explicit time step for a given parabolic system based on the CFL stability
condition.
is an explicit time step for a given parabolic system based on the CFL stability
condition. 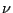 (nuSTS) is a free parameter less than unity. For
(nuSTS) is a free parameter less than unity. For
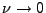 , STS is asymptotically
, STS is asymptotically
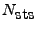 times faster than the conventional explicit scheme based on the CFL condition.
During the
times faster than the conventional explicit scheme based on the CFL condition.
During the 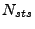 sub-time steps, the STS method still solves
solutions at each intermediate step
sub-time steps, the STS method still solves
solutions at each intermediate step 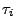 ; however,
such solutions should not be considered as meaningful solutions.
; however,
such solutions should not be considered as meaningful solutions.
Extended from the original STS method for accelerating parabolic timestepping,
our STS method advances advection and/or diffusion (hyperbolic and/or parabolic) system of equations.
This means that the STS algorithm in FLASH invokes
a single
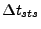 for both advection and diffusion,
and does not use any sub-cycling for diffusion based on a given advection time step.
In this case,
for both advection and diffusion,
and does not use any sub-cycling for diffusion based on a given advection time step.
In this case, 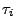 is given by
is given by
![$\displaystyle \tau_i=\Delta t_{\mbox{CFL}}\big[ (-1+\nu_{\mbox{sts}}) cos\big(\frac{\pi(2j-1)}{2N_{\mbox{sts}}} + 1+\nu_{\mbox{sts}} \big)\big]^{-1},$](img156.png) |
(7.2) |
where
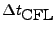 can be an explicit time step for advection (
can be an explicit time step for advection (
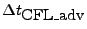 )
or parabolic (
)
or parabolic (
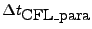 ) systems.
In cases of advection-diffusion system,
) systems.
In cases of advection-diffusion system,
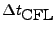 takes (
takes (
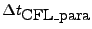 ) when it is smaller
than (
) when it is smaller
than (
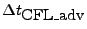 ); otherwise, FLASH's timestepping will proceed without using STS iterations (i.e.,
using standard explicit timestepping that is either Strang split evolution or unsplit evolution.
); otherwise, FLASH's timestepping will proceed without using STS iterations (i.e.,
using standard explicit timestepping that is either Strang split evolution or unsplit evolution.
Since the method is explicit, it works equally well
on both a uniform grid and AMR grids without modification.
The STS method is first-order accurate in time.
Both directionally-split and unsplit hydro solvers can use the STS method,
simply by invoking a runtime parameter useSTS = .true. in flash.par.
There are couple of runtime parameters that control solution accuracy and stability.
They are decribed in Table 7.1.
Table 7.1:
Runtime parameters for STS
| Variable |
Type |
Default |
Description |
| useSTS |
logical |
.false. |
Enable STS |
| nstepTotalSTS |
integer |
5 |
Suggestion:  5 for hyperbolic; 5 for hyperbolic;  10 for parabolic 10 for parabolic |
| nuSTS |
real |
0.2 |
Suggestion:  0.2 for hyperbolic; 0.2 for hyperbolic; 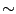 0.01 for parabolic. It is known that a very low value of 0.01 for parabolic. It is known that a very low value of 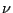 may result in unstable temporal integrations, while a value close to unity can decrease the expected efficiency of STS. may result in unstable temporal integrations, while a value close to unity can decrease the expected efficiency of STS. |
| useSTSforDiffusion |
logical |
.false. |
This setup will use the STS for overcoming small diffusion time steps assuming
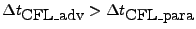 . In implementation, it will set . In implementation, it will set
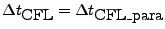 in Eqn. 7.2. Do not allow to turn on this switch when there is no diffusion (viscosity, conductivity, and magnetic resistivity) used. in Eqn. 7.2. Do not allow to turn on this switch when there is no diffusion (viscosity, conductivity, and magnetic resistivity) used. |
| allowDtSTSDominate |
logical |
.false. |
If true, this will allow to have
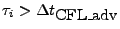 , which may result in unstable integrations. , which may result in unstable integrations. |
The Driver unit supplies certain runtime parameters regardless of
which type of driver is chosen. These are described in the
online Runtime Parameters Documentation page.
FLASH3 Transition:
The
Driver unit no longer provides runtime parameters,
physical constants, or logfile management. Those services have been
placed in separate units. The
Driver unit also does not declare
boolean values to include a unit in a simulation or not. For example,
in FLASH2, the
Driver declared a runtime parameter
iburn to turn on and off
burning.
if(iburn) then
call burning ....
end if
In FLASH4 the individual unit declares a runtime parameter that
determines whether the unit is used during the simulation
e.g., the
Burn unit declares
useBurn within the
Burn unit code that
turns burning on or off. This way the
Driver is no longer responsible for knowing what is included in a simulation.
A unit gets called from the
Driver, and if it is not included in a simulation, a stub gets called.
If a unit, like
Burn, is included but the user wants to turn burning off, then the runtime parameter
declared in the
Burn unit would be set to false.
Finally, the the Driver unit calls Driver_finalizeFlash which calls the finalize routines for each unit. Typically this involves deallocating memory and any other necessary cleanup.
In FLASH4 the Driver unit also provides a number of
accessor functions to get data stored in the Driver unit, for
example Driver_getDt, Driver_getNStep,
Driver_getElapsedWCTime, Driver_getSimTime.
FLASH3 Transition:
In FLASH4 most of the quantities that were in the FLASH2 database are stored in the
Grid unit or are replaced with functionality in the Flash.h file. A few scalars
quantities like dt, the current timestep number nstep, simulation time and elapsed
wall clock time, however, are now stored in the Driver_data FORTRAN90 module.
The Driver unit API also defines two interfaces for halting the code,
Driver_abortFlash and
Driver_abortFlashC.c.
The 'c' routine
version is available for calls written in C, so that the user does not have to worry about
any name mangling. Both of these routines print an error message and
call MPI_Abort.
The Driver unit is responsible for determining the time step 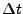 that is used to advance the solution from time
that is used to advance the solution from time 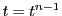 to
to 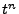 .
At startup, a tentative
.
At startup, a tentative 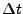 is chosen based in runtime parameters,
in particular dtinit.
The routine Driver_verifyInitDt (usually invoked from Driver_initFlash) is used to check and,
if necessary, modify the initial
is chosen based in runtime parameters,
in particular dtinit.
The routine Driver_verifyInitDt (usually invoked from Driver_initFlash) is used to check and,
if necessary, modify the initial 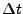 .
Subsequently, the routine Driver_computeDt (usually invoked from Driver_evolveFlash at the end
of an iteration of the main evolution loop) is used to recompute
.
Subsequently, the routine Driver_computeDt (usually invoked from Driver_evolveFlash at the end
of an iteration of the main evolution loop) is used to recompute 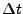 for the next evolution step.
for the next evolution step.
The implementation of Driver_computeDt can lower or increase the
time step. It takes various runtime parameters into consideration,
including
dtmin,
dtmax, and
tstep_change_factor.
For the most part, however, Driver_computeDt calls on
UNIT_computeDt routines of various code units to query those
units for their time step requirements, and usually chooses the smallest
time step that is acceptable to all units queried.
The code units that participate in this negotiation return a 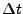 ,
and usually some additional information about which location in the
simulaton domain caused the reequired step to be as low as returned.
A unit's time step requirement can depend on the current state of the
solution as well as on further runtime parameters.
For example, the dt returned by Hydro_computeDt
depends on the state of density, pressure, and velocities (and possibly
additional variables) in the cells of the domain, as well as on
the runtime parameter cfl.
,
and usually some additional information about which location in the
simulaton domain caused the reequired step to be as low as returned.
A unit's time step requirement can depend on the current state of the
solution as well as on further runtime parameters.
For example, the dt returned by Hydro_computeDt
depends on the state of density, pressure, and velocities (and possibly
additional variables) in the cells of the domain, as well as on
the runtime parameter cfl.
7.1.5.1 Generic time step limiting for positive definiteness
A generic method for limiting time steps, based on a requirement that certain (user-specified)
variables should never become negative, has been added in FLASH4.5.
To understand the basic idea, think of each variable that this limiter is applied
to as a density of some quantity 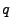 . (Variables of PER_MASS type are actually converted to
their PER_VOLUME counterparts in the implementation of the method.)
. (Variables of PER_MASS type are actually converted to
their PER_VOLUME counterparts in the implementation of the method.)
The algorithm is based on examining the distribution of 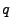 in neighboring cells,
and making for each cell a near-worst-case estimate of the rate of depletion
in neighboring cells,
and making for each cell a near-worst-case estimate of the rate of depletion 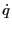 based on projected fluxes of
based on projected fluxes of 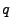 out of the cell over its faces.
This can be applied to any variable, it is not required that the variable
represents any quantity that is actually advected as described.
See Table 7.2 for how to use.
This feature may be particularly useful when applied to "eion" in
multidimensional 3T simulations in order to avoid some kinds of “negative ion temperature”
failures, as an alternative to lowering the Hydro runtime parameter cfl.
out of the cell over its faces.
This can be applied to any variable, it is not required that the variable
represents any quantity that is actually advected as described.
See Table 7.2 for how to use.
This feature may be particularly useful when applied to "eion" in
multidimensional 3T simulations in order to avoid some kinds of “negative ion temperature”
failures, as an alternative to lowering the Hydro runtime parameter cfl.
Table 7.2:
Runtime parameters for positive definiteness.
| Parameter |
Type |
Default |
Description |
| dr_usePosdefComputeDt |
boolean |
.false. |
Set to .true. to turn
positive-definite time step limiter on. |
| |
|
|
|
| dr_numPosdefVars |
integer |
4 |
Number of variables for which positive definiteness
should be enforced |
| |
|
|
|
| dr_posdefVar_N |
string |
"none" |
Name of Nth variable for positive-definite dt limiter |
| |
|
|
|
| dr_posdefDtFactor |
real |
1.0 |
Scaling factor for dt limit from positive-definite time step limiter.
Similar to CFL factor. If set to -1, use CFL factor from Hydro. |
![]() using two properties of stability and optimality in
Chebychev polynomial of degree
using two properties of stability and optimality in
Chebychev polynomial of degree ![]() . These properties optimally
maximize the time step
. These properties optimally
maximize the time step
![]() by which a solution vector can be
evolved. A stability condition is imposed only after each time
step
by which a solution vector can be
evolved. A stability condition is imposed only after each time
step
![]() , which is further subdivided into smaller
, which is further subdivided into smaller
![]() sub-time steps,
sub-time steps, ![]() , that is,
, that is,
![]() , where
the sub-time step is given by
, where
the sub-time step is given by
![]() for both advection and diffusion,
and does not use any sub-cycling for diffusion based on a given advection time step.
In this case,
for both advection and diffusion,
and does not use any sub-cycling for diffusion based on a given advection time step.
In this case, ![]() is given by
is given by
![]() ,
and usually some additional information about which location in the
simulaton domain caused the reequired step to be as low as returned.
A unit's time step requirement can depend on the current state of the
solution as well as on further runtime parameters.
For example, the dt returned by Hydro_computeDt
depends on the state of density, pressure, and velocities (and possibly
additional variables) in the cells of the domain, as well as on
the runtime parameter cfl.
,
and usually some additional information about which location in the
simulaton domain caused the reequired step to be as low as returned.
A unit's time step requirement can depend on the current state of the
solution as well as on further runtime parameters.
For example, the dt returned by Hydro_computeDt
depends on the state of density, pressure, and velocities (and possibly
additional variables) in the cells of the domain, as well as on
the runtime parameter cfl.
![]() in neighboring cells,
and making for each cell a near-worst-case estimate of the rate of depletion
in neighboring cells,
and making for each cell a near-worst-case estimate of the rate of depletion ![]() based on projected fluxes of
based on projected fluxes of ![]() out of the cell over its faces.
This can be applied to any variable, it is not required that the variable
represents any quantity that is actually advected as described.
See Table 7.2 for how to use.
This feature may be particularly useful when applied to "eion" in
multidimensional 3T simulations in order to avoid some kinds of “negative ion temperature”
failures, as an alternative to lowering the Hydro runtime parameter cfl.
out of the cell over its faces.
This can be applied to any variable, it is not required that the variable
represents any quantity that is actually advected as described.
See Table 7.2 for how to use.
This feature may be particularly useful when applied to "eion" in
multidimensional 3T simulations in order to avoid some kinds of “negative ion temperature”
failures, as an alternative to lowering the Hydro runtime parameter cfl.