Next: 18.3 Stir Unit Up: 18. Local Source Terms Previous: 18.1 Burn Unit Contents Index
The analysis of UV and X-ray observations, and in particular of spectral lines, is a powerful diagnostic tool of the physical conditions in astrophysical plasmas (e.g., the outer layers of the solar atmosphere, supernova remnants, etc.). Since deviation from equilibrium ionization may have a non-negligible effect on the UV and X-ray lines, it is crucial to take into account these effects in the modeling of plasmas and in the interpretation of the relevant observations.
In light of the above observations, FLASH contains the unit Ionize, in particular the implementation physics/sourceTerms/Ionize/IonizeMain/Nei, which is capable of computing the density of each ion species of a given element taking into account non-equilibrium ionization (NEI). This is accomplished by solving a system of equations consisting of the fluid equations of the whole plasma and the continuity equations of the ionization species of the elements considered. The densities of the twelve most abundant elements in astrophysical material (He, C, N, O, Ne, Mg, Si, S, Ar, Ca, Fe, and Ni) plus fully ionized hydrogen and electrons can be computed by this unit.
The Euler equations plus the set of advection equations for all the
ion species take the following form
| (18.25) |
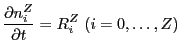 |
(18.26) |
Note that in the present version, the contribution of the ionization and recombination to the energy equation (the bracketed term in (18.23)) is not accounted for. Also, it should be noted that the source term in the NEI unit implementation is adequate to solve the problem for optically thin plasma in the “coronal” approximation; just collisional ionization, auto-ionization, radiative recombination, and dielectronic recombination are considered.
In order to run a FLASH executable that uses the ionization unit, the ionization coefficients of Summers (1974) must be contained in a file named summers_den_1e8.rates in the same directory as the executable when the simulation is run. This file is copied into the object/ directory with the Config keyword DATAFILES in the physics/sourceTerms/Ionize/IonizeMain implementation.
The Ionize unit supplies the runtime
parameters described in Table 18.1.
The Ionize unit requires that the subunit implementation Simulation/SimulationComposition/Ionize be used to set up the ion species of the fluid. The ions are defined in a file Simulation/SimulationComposition/Ionize/SpeciesList.txt, however, the Config file in the simulation directory (e.g. Simulation/SimulationMain/Neitest/Config) defines which subset of these elements are to be used.