Next: 35.5 Burn Test Problem Up: 35. The Supplied Test Previous: 35.3 Gravity Test Problems Contents Index
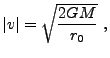 |
(35.47) |
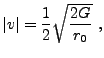 |
(35.48) |
|
No specific gravity unit is required by the problem configuration file, because the problem is intended to be run with either a fixed external field or the particles' own field. If the particles are to orbit in an external field (ext_field = .true.), the field is assumed to be a central point-mass field (physics/Gravity/GravityMain/PointMass), and the parameters for that unit should be assigned appropriate values. If the particles are self-gravitating (ext_field = .false.), the physics/Gravity/GravityMain/Poisson unit should be included in the code, and a Poisson solver that supports isolated boundary conditions should be used (grav_boundary_type = "isolated").
In either case, long-range forces for the particles must be turned on, or else they will not experience any accelerations at all. This can be done using the particle-mesh method by including the unit Particles/ParticlesMain/active/longRange/gravity/ParticleMesh.
As of FLASH 2.1 both the multigrid and multipole solvers support isolated boundary conditions. This problem should be run in three dimensions.
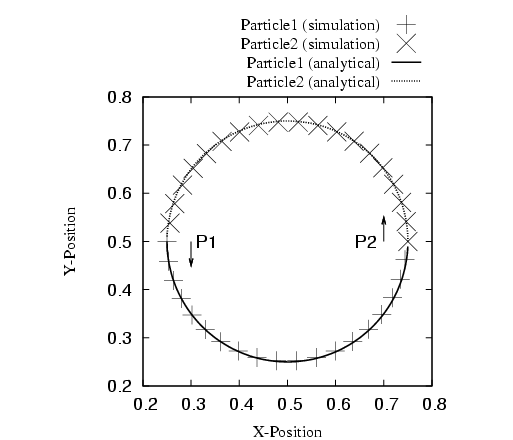
The two-particle orbit problem uses the runtime parameters listed in Table 35.13 in addition to the regular ones supplied with the code.
The cosmological pancake problem (Zel'dovich 1970),
Pancake, provides a good
simultaneous
test of the hydrodynamics, particle dynamics, Poisson solver, and
cosmological expansion modules. Analytic
solutions well into the nonlinear regime are available for both
![]() -body and hydrodynamical codes
(Anninos & Norman 1994), permitting an assessment of the code's accuracy.
After caustic formation the problem provides a stringent test of the code's
ability to track thin, poorly resolved features and strong shocks using
most of the basic physics needed for cosmological problems. Also, as pancakes
represent single-mode density perturbations, coding this test problem is
useful as a basis for creating more complex cosmological initial conditions.
-body and hydrodynamical codes
(Anninos & Norman 1994), permitting an assessment of the code's accuracy.
After caustic formation the problem provides a stringent test of the code's
ability to track thin, poorly resolved features and strong shocks using
most of the basic physics needed for cosmological problems. Also, as pancakes
represent single-mode density perturbations, coding this test problem is
useful as a basis for creating more complex cosmological initial conditions.
We set the initial conditions for the pancake problem in the
linear regime using the
analytic solution given by Anninos and Norman (1994). In a universe with
![]() at redshift
at redshift ![]() , a perturbation
of wavenumber
, a perturbation
of wavenumber ![]() which collapses to a caustic at redshift
which collapses to a caustic at redshift ![]() has
comoving density and velocity given by
has
comoving density and velocity given by
Dark matter particles are initialized using the same solution as the
gas. The Lagrangian coordinates ![]() are assigned to lie on a
uniform grid. The corresponding perturbed coordinates
are assigned to lie on a
uniform grid. The corresponding perturbed coordinates ![]() are
computed using (35.51). Particle velocities are
assigned using (35.50).
are
computed using (35.51). Particle velocities are
assigned using (35.50).
At caustic formation (![]() ), planar shock waves form in the gas
on either side
of the pancake midplane and begin to propagate outward. A small region
at the midplane is left unshocked. Immediately behind the shocks, the
comoving density and temperature vary approximately as
), planar shock waves form in the gas
on either side
of the pancake midplane and begin to propagate outward. A small region
at the midplane is left unshocked. Immediately behind the shocks, the
comoving density and temperature vary approximately as
 |
(35.53) | ||
 |
![$\displaystyle \bar{\rho}\left[{1+z_{\rm fid}\over 1+z}\right]^3
\left[{3H_0^2\m...
...}
{\left(1+z_c\right)^4\left(1+z\right)^3\over
1+z_{\rm fid}}\right]^{1/\gamma}$](img3979.png) |
(35.54) | ||
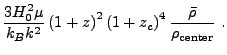 |
|
Because they are collisionless, the particles behave very differently than the gas. As particles accelerate toward the midplane, their phase profile develops a backwards “S” shape. At caustic formation the velocity becomes multivalued at the midplane. The region containing multiple streams grows in size as particles pass through the midplane. At the edges of this region (the caustics, or the inflection points of the “S”), the particle density is formally infinite, although the finite force resolution of the particles keeps the height of these peaks finite. Some of the particles that have passed through the midplane fall back and form another pair of caustics, twisting the phase profile again. Because each of these secondary caustics contains five streams of particles rather than three, the second pair of density peaks are higher than the first pair. This caustic formation process repeats arbitrarily many times in the analytic solution. In practice, the finite number of particles and the finite force resolution limit the number of caustics that are observed. An example FLASH calculation of the post-caustic particle solution appears in Figure 35.69.

|
The 2D pancake problem in FLASH4 uses the runtime parameters listed in Table 35.14 in addition to the regular ones supplied with the code.
This problem uses periodic boundary conditions and is intrinsically one-dimensional, but it can be run using Cartesian coordinates in 1D, 2D, or 3D, with the pancake midplane tilted with respect to the coordinate axes if desired.
In the PoisParticles problem, the density stored in the grid is used as an indicator of where to create new particles. Here, the number of particles created in each region of the grid is proportional to the grid density, i.e., more particles are created in regions where there is a high density. Each new particle is assigned a mass, which is taken from the density in the grid, so that mass is conserved.
The flash.par parameters shown in Table 35.15 specify that the grid should refine until at most 5 particles exist per block. This creates a refined grid similar to the Poistest problem.
| Variable | Type | Value | Description |
| refine_on_particle_count | logical | .true. | On/Off flag for refining the grid according to particle count. |
| max_particles_per_blk | integer | 5 | Grid refinement criterion which specifies maximum number of particles per block. |